Benutzer:Ansgar WWU-6/Anwendungsaufgaben

Anwendungsaufgaben

Aufgabe: Elternsprechtag

Datei:Parking-825371 1920.jpg

Jedes halbe Jahr veranstaltet die Gesamtschule einen Elternsprechtag von 12 Uhr bis 18 Uhr. Da den Eltern nur eine begrenzte Anzahl an Parkplätzen zur Verfügung steht, muss die Schulleitung rechtzeitig entscheiden, ob weitere Parkplätze angemietet werden müssen. Dabei kann angenommen werden, dass die ersten Parkplätze erst ab 12 Uhr belegt werden und spätestens um 18 Uhr das letzte Auto vom Parkplatz gefahren ist. Für diesen Elternsprechtag stehen den Eltern 50 Parkplätze zur Verfügung. Eine Stunde nach Beginn des Elternsprechtages ist bereits die Hälfte der Parkplätze belegt.

a)

Aus Erfahrung lässt sich die Anzahl belegter Parkplätze in Abhängigkeit zur Uhrzeit ($t$ in Stunden, beginnend mit $t = 0$ für 12 Uhr) durch eine quadratische Funktion der Form $f(t) = at^2 + bt + c$ beschreiben. Löse zunächst den folgenden Lückentext und stelle anschließend mit dessen Hilfe die Gleichung von $f$ auf.

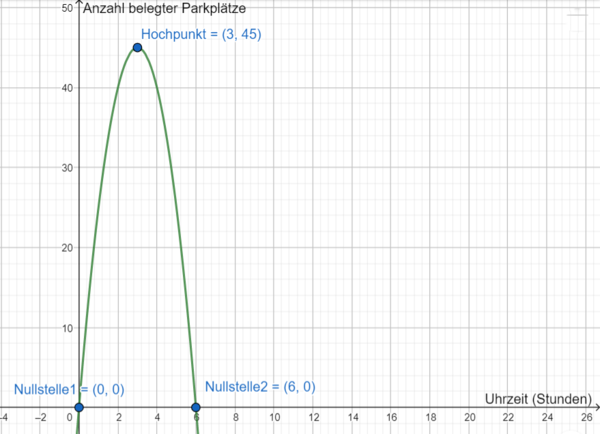
Um die drei Unbekannten $a$, $b$ und $c$ eindeutig zu bestimmen, benötigt man drei Bedingungen aus den Informationen. Der Graph hat bei entsprechender Wahl der Einheiten eine Nullstelle bei $t=0$. Demnach ist die erste Bedingung $f ( 0 ) = 0$. Er verläuft außerdem durch den Punkt $(1 | 25)$, sodass die zweite Bedingung $f ( 1 ) = 25$ ist. Bei $t = 6$ hat der Graph eine weitere Nullstelle und deshalb ist die dritte Bedingung $f ( 6 ) = 0$.

Um die drei Unbekannten $a$, $b$ und $c$ eindeutig zu bestimmen, benötigst du drei Bedingungen aus den Informationen.

Der Graph hat bei entsprechender Wahl der Einheiten eine Nullstelle bei $t = 0$, er verläuft durch den Punkt $(1 | 25)$ und hat eine weitere Nullstelle bei $t = 6$

$f(0) = 0$, $f(1) = 25$, $f(6)=0$

$f(t) = -5t^2 + 30t$

$\begin{array}{rlll} f(t) &=& at^2 + bt + c \\ \end{array}$



$\begin{array}{rlll} &&f(0) &=& 0 \\ &\Leftrightarrow& a \cdot 0^2 + b \cdot 0 + c &=& 0 \\ &\Leftrightarrow& c &=& 0 \\ \end{array}$



$\Rightarrow f(t) = at^2 + bt$



$\begin{array}{rlll} &&f(1) &=& 25 \\ &\Leftrightarrow& a \cdot 1^2 + b \cdot 1 &=& 25 \\ &\Leftrightarrow& a + b &=& 25 \\ \end{array}$



$\begin{array}{rlll} &&f(6) &=& 0 \\ &\Leftrightarrow& a \cdot 6^2 + b \cdot 6 &=& 0 \\ &\Leftrightarrow& 36a + 6b &=& 0 \\ \end{array}$





Insgesamt erhalten wir also folgendes Gleichungssystem:

$\begin{array}{rlll} &I\quad& a + b &=& 25 \\ &II\quad& 36a + 6b &=& 0 \\ \end{array}$

Dieses Gleichungssystem lösen wir mit dem Einsetzungsverfahren:

Als erstes stellen wir Gleichung $I$ nach $a$ um und erhalten

$\begin{array}{rlll} &I\quad& a = 25 - b \\ \end{array}$

Setzen wir diese (umgeformte) Gleichung $I$ in Gleichung $II$ ein, erhalten wir

$\begin{array}{rlll} &II\quad&&& 36a + 6b &=& 0 &\mid a = 25 - b \, \textrm{einsetzen} \\ &&&\Rightarrow& 36 \cdot (25 - b) + 6b &=& 0 &\mid \textrm{Ausmultiplizieren} \\ &&&\Rightarrow& 900 - 36b + 6b &=& 0 \\ &&&\Rightarrow& 900 - 30b &=& 0 &\mid + 30b \\ &&&\Rightarrow& 30b &=& 900 &\mid : 30 \\ &&&\Rightarrow& b &=& 30 \\ \end{array}$

Setzen wir $b = 30$ in die (umgeformte) Gleichung $I$ ein, erhalten wir

$\begin{array}{rlll} &I&&& a &=& 25 - b &\mid b = 30 \, \textrm{einsetzen} \\ &&&\Rightarrow& a &=& 25 - 30 \\ &&&\Rightarrow& a &=& -5 \\ \end{array}$

und damit insgesamt

$f(t) = -5t^2 + 30t$

b)

Entscheide, ob die 50 Parkplätze für die gesamte Dauer des Elternsprechtages ausreichend sind oder zusätzliche Parkplätze angemietet werden müssen.

Damit die Parkplätze ausreichen, dürfen maximal 50 Parkplätze zu einer bestimmten Uhrzeit belegt sein. Hat die Funktion einen Hochpunkt mit einem Funktionswert kleiner gleich 50, so ist sie nirgendwo größer als dort.

$\begin{array}{rlll} &\textrm{notwendige} \, \textrm{Bedingung:}& f'(t) &=& 0 \\ &\textrm{hinreichende} \, \textrm{Bedingung:}& f''(t) &<& 0 \\ \end{array}$

Der Graph der Funktion $f$ hat den Hochpunkt $(3 | 45)$. Die maximale Anzahl belegter Parkplätze ist also um 15 Uhr nachzuweisen. Zu der Zeit sind 45 Parkplätze belegt, sodass die vorhandenen 50 Parkplätze ausreichen.

$\begin{array}{rlll} f(t) &=& -5t^2 + 30t \\ f'(t) &=& -10t + 30 \\ f''(t) &=& -10 \\ \end{array}$

$\begin{array}{rlll} \textrm{Notwendige Bedingung:} && f'(t) &=& 0 \\ &\Leftrightarrow& -10t + 30 &=& 0 &\mid + 10t\\ &\Leftrightarrow& 10t &=& 30 &\mid : 10 \\ &\Leftrightarrow& t &=& 3 \\ \end{array}$



$\begin{array}{rlll} \textrm{Hinreichende Bedingung:} &&f'(3) &=& 0 &&\textrm{und} \\ &&f''(3) &=& -10 &<& 0 \end{array}$

$f(3)=-5 \cdot 3^2 + 30 \cdot 3 = 45$

c)

Skizziere nun den Graphen von $f$ anhand der Informationen. Beachte hierbei die geeignete Wahl der Einheiten.

Aufgabe: Virusinfektion

Im Januar befällt ein neuartiges Virus Deutschland. Mittlerweile ist es Oktober und du suchst im Internet nach Informationen über die Infektionszahlen. Dort triffst du auf folgende Informationen:

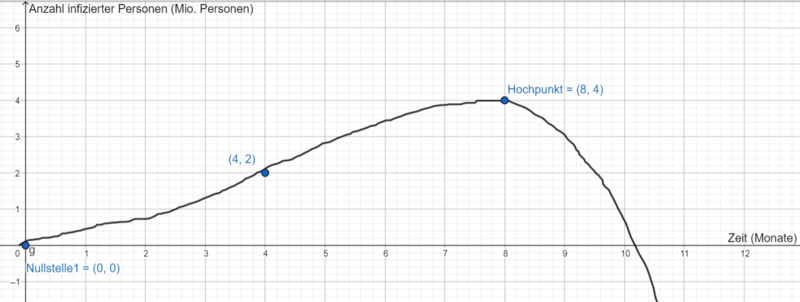
• Im Dezember des Vorjahres befinden sich noch keine infizierten Personen in Deutschland
• Im April leben 2.000.000 infizierte Personen in Deutschland
• Im August leben 4.000.000 infizierte Personen in Deutschland
• Durch entsprechende Maßnahmen ist die Zahl infizierter Personen ab August rückläufig

a)

Stelle alle relevanten Informationen in einem geeigneten Koordinatensystem graphisch dar und skizziere einen möglichen Graphen. Beachte hierbei die geeignete Wahl der Einheiten.

Kann man den Monaten Zahlen zuweisen, um sie entlang einer Achse anzuordnen? Welche Einheit ist für die Anzahl infizierter Personen geeignet?

Der Graph hat bei entsprechender Wahl der Einheiten eine Nullstelle bei $t = 0$, er verläuft durch den Punkt $(4 | 2)$ und hat den Hochpunkt $(8 | 4)$

Unterer Graph ist nur eine Möglichkeit einer ungefähren Modellierung der Virusinfektion!

b)

Die Anzahl infizierter Personen lässt sich durch eine kubische Funktion der Form $f(t) = at^3 + bt^2 + ct + d$ beschreiben. Stelle die Gleichung von $f$ auf.

Um die vier Unbekannten $a$,$b$,$c$ und $d$ eindeutig zu bestimmen, benötigst du vier Bedingungen aus den Informationen. Nutze dafür Teilaufgabe a).

$f(0) = 0$, $f(4) = 2$, $f(8)=4$, $f'(8)=0$

$f(t) = -\frac{1}{64} t^3 + \frac{3}{16} t^2 = \frac{1}{64} (-t^3 + 12t^2)$

$\begin{array}{rlll} f(t) &=& at^3 + bt^2 + ct + d \\ f'(t) &=& 3at^2 + 2bt + c \\ \end{array}$



$\begin{array}{rlll} &&f(0) &=& 0 \\ &\Leftrightarrow& a \cdot 0^3 + b \cdot 0^2 + c \cdot 0 + d &=& 0 \\ &\Leftrightarrow& d &=& 0 \\ \end{array}$



$\Rightarrow f(t) = at^3 + bt^2 + ct$



$\begin{array}{rlll} &&f(4) &=& 2 \\ &\Leftrightarrow& a \cdot 4^3 + b \cdot 4^2 + c \cdot 4 &=& 2 \\ &\Leftrightarrow& 64a + 16b + 4c &=& 2 \\ \end{array}$



$\begin{array}{rlll} &&f(8) &=& 4 \\ &\Leftrightarrow& a \cdot 8^3 + b \cdot 8^2 + c \cdot 8 &=& 4 \\ &\Leftrightarrow& 512a + 64b + 8c &=& 4 \\ \end{array}$



$\begin{array}{rlll} &&f'(8) &=& 0 \\ &\Leftrightarrow& 3a \cdot 8^2 + 2b \cdot 8 + c &=& 0 \\ &\Leftrightarrow& 192a + 16b + c &=& 0 \\ \end{array}$





Insgesamt erhalten wir also folgendes Gleichungssystem:

$\begin{array}{rlll} &I\quad& &64a& + &16b& + &4c& &=& &2& \\ &II\quad& &512a& + &64b& + &8c& &=& &4& \\ &III\quad& &192a& + &16b& + &1c& &=& &0& \\ \end{array}$

Dieses Gleichungssystem lösen wir mit dem Gauß-Verfahren:

$II - 8 \cdot I$

$\begin{array}{rlll} &I\quad& &64a& + &16b& + &4c& &=& &2& \\ &II\quad& && - &64b& - &24c& &=& &-12& \\ &III\quad& &192a& + &16b& + &1c& &=& &0& \\ \end{array}$



$III - 3 \cdot I$

$\begin{array}{rlll} &I\quad& &64a& + &16b& + &4c& &=& &2& \\ &II\quad& && - &64b& - &24c& &=& &-12& \\ &III\quad& && - &32b& - &11c& &=& &-6& \\ \end{array}$



$III - \frac{1}{2} \cdot II$

$\begin{array}{rlll} &I\quad& &64a& + &16b& + &4c& &=& &2& \\ &II\quad& && - &64b& - &24c& &=& &-12& \\ &III\quad& && && &21c& &=& &0& \\ \end{array}$



Gleichung $III$ liefert uns nun

$\begin{array}{rlll} &III\quad&&& 21c &=& 0 &\mid : 21 \\ &&&\Rightarrow& c &=& 0 \\ \end{array}$

Setzen wir $c = 0$ in Gleichung $II$ ein, erhalten wir

$\begin{array}{rlll} &II\quad&&& -64b + 24c &=& -12 &\mid c = 0 \, \textrm{einsetzen} \\ &&&\Rightarrow& -64b + 24 \cdot 0 &=& -12 \\ &&&\Rightarrow& -64b &=& -12 &\mid : (-64) \\ &&&\Rightarrow& b &=& \frac{3}{16} \\ \end{array}$

Setzen wir $c = 0$ und $b = \frac{3}{16}$ in Gleichung $I$ ein, erhalten wir

$\begin{array}{rlll} &I\quad&&& 64a + 16b + 4c &=& 2 &\mid c = 0 \, \textrm{und} \, b = \frac{3}{16} \, \textrm{einsetzen}\\ &&&\Rightarrow& 64a + 16 \cdot \frac{3}{16} + 4 \cdot 0 &=& 2 \\ &&&\Rightarrow& 64a + 3 &=& 2 &\mid -3 \\ &&&\Rightarrow& 64a &=& -1 &\mid : 64 \\ &&&\Rightarrow& a &=& -\frac{1}{64} \\ \end{array}$



und damit insgesamt

$f(t) = -\frac{1}{64} t^3 + \frac{3}{16} t^2 = \frac{1}{64} (-t^3 + 12t^2)$

c)

Forscher gehen nun (im Oktober) davon aus, dass noch im selben Jahr alle jemals infizierten Personen in Deutschland geheilt sind und entsprechend keine Fälle mehr in Deutschland auftreten. Prüfe diese Vorhersage anhand der Informationen.

Zu den Zeitpunkten, zu denen keine infizierten Personen in Deutschland leben, hat der Graph seine Nullstellen.

Gleichungen, die nur Summanden mit der Variable $t$ enthalten, lassen sich durch Faktorisieren lösen .

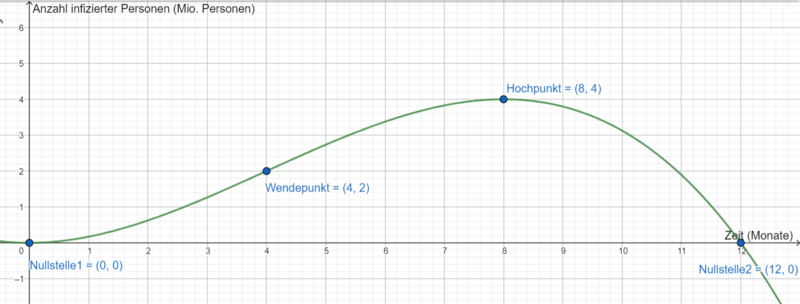
$f$ hat Nullstellen bei $t_{1} = 0$ und $t_{2} = 12$. Im Dezember treten also keine infizierten Fälle mehr in Deutschland auf, sodass alle jemals infizierten Personen in Deutschland noch im selben Jahr geheilt sind. Die Vorhersage ist demnach richtig.

$\begin{array}{rlll} &&f(t) &=& 0 \\ &\Leftrightarrow& \frac{1}{64} (-t^3 + 12t^2) &=& 0 &\mid :\frac{1}{64} \\ &\Leftrightarrow& -t^3 + 12t^2 &=& 0 &\mid \textrm{Faktorisieren} \\ &\Leftrightarrow& t^2 (-t + 12) &=& 0 \\ &\Rightarrow& t^2 = 0 & \textrm{und}& && -t + 12 &=& 0 \\ &\Leftrightarrow& t_{1} = 0 & \textrm{und}& && t_{2} &=& 12 \\ \end{array}$

d)

Forscher behaupten weiterhin, dass die milden Temperaturen im Frühling dafür sorgen, dass sich der temperaturempfindliche Virus optimal ausbreiten kann und deshalb die stärkste Zunahme infizierter Personen im Frühling nachzuweisen ist. Prüfe diese Behauptung anhand der Informationen.

Der Wendepunkt ist der Punkt der stärksten Zunahme (oder stärksten Abnahme) des Funktionsgraphen, der an dieser Stelle sein Krümmungsverhalten ändert.

$\begin{array}{rlll} &\textrm{notwendige} \, \textrm{Bedingung:}& f''(t) &=& 0 \\ &\textrm{hinreichende} \, \textrm{Bedingung:}& f'''(t) &\neq& 0 \\ \end{array}$

Der Graph der Funktion $f$ hat einen Wendepunkt bei $t = 4$. Die stärkste Zunahme infizierter Personen ist also im April (bzw. im Frühling) nachzuweisen. Die Behauptung ist demnach richtig.

$\begin{array}{rlll} f(t) &=& -\frac{1}{64} t^3 + \frac{3}{16} t^2 \\ f'(t) &=& -\frac{3}{64} t^2 + \frac{3}{8} t \\ f''(t) &=& -\frac{3}{32} t + \frac{3}{8} \\ f'''(t) &=& -\frac{3}{32} \\ \end{array}$

$\begin{array}{rlll} \textrm{Notwendige} \, \textrm{Bedingung:} && f''(t) &=& 0 \\ &\Leftrightarrow& -\frac{3}{32} t + \frac{3}{8} &=& 0 &\mid +\frac{3}{32} t\\ &\Leftrightarrow& \frac{3}{32} t &=& \frac{3}{8} &\mid :\frac{3}{32} \\ &\Leftrightarrow& t &=& 4 \\ \end{array}$

$\begin{array}{rlll} \textrm{Hinreichende} \, \textrm{Bedingung:} &&f''(4) &=& 0 &&\textrm{und} \\ &&f'''(4) &=& -\frac{3}{32} &\neq& 0 \end{array}$

e)

Skizziere nun den Graphen von $f$ anhand der Informationen und vergleiche ihn mit dem Graphen aus Teilaufgabe a). Für welchen Zeitraum ist dieser Graph als mathematische Modellierung der Virusinfektion geeignet?

Da die Funktionswerte von $f$ für $t > 12$ negativ sind, ist der Graph nur für $0 \leq t \leq 12$ als mathematische Modellierung der Virusinfektion geeignet.