Benutzer:Buss-Haskert/Terme 8E
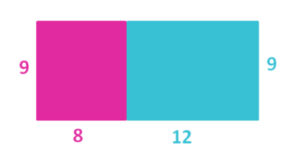
Flächeninhalte mit Termen beschreiben
1. Ausmultiplizieren und Ausklammern (• vor der Klammer )
Vergleiche deine Ideen mit denen im nachfolgenden Video:
Wie lautet der Name dieses Gesetzes? Notiere dies als Überschrift über die obige Zeichnung in dein Heft.
Dieses Gesetz wird im folgenden GeoGebra-Applet noch einmal veranschaulicht. Du kannst die Zahlen durch Variablen ersetzen, indem du die Häkchen "Variable anzeigen" auswählst.
Originallink: https://www.geogebra.org/m/XcFmnc9X

Applet von Birgit Lachner
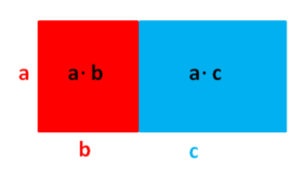
Das Verteilungsgesetz lässt sich auf das Rechnen mit Variablen und Termen übertragen:
Auch hier ist das große Rechteck aus den kleinen Flächen zusammengesetzt. Der Flächeninhalt kann auf zwei Arten angegeben werden:
als Produkt der Seitenlängen a ⋅ ⟨b+c⟩ und als Summe der einzelnen Flächen a⋅b + a⋅c
Es gilt also: a⋅(b+c) = a⋅b + a⋅c.