Merke
Sind bei einem mehrstufigen Zufallsversuch die Wahrscheinlichkeiten auf jeder Stufe gleich groß, so ist der Versuch ein mehrstufiger Laplace-Versuch.
Beispiel:
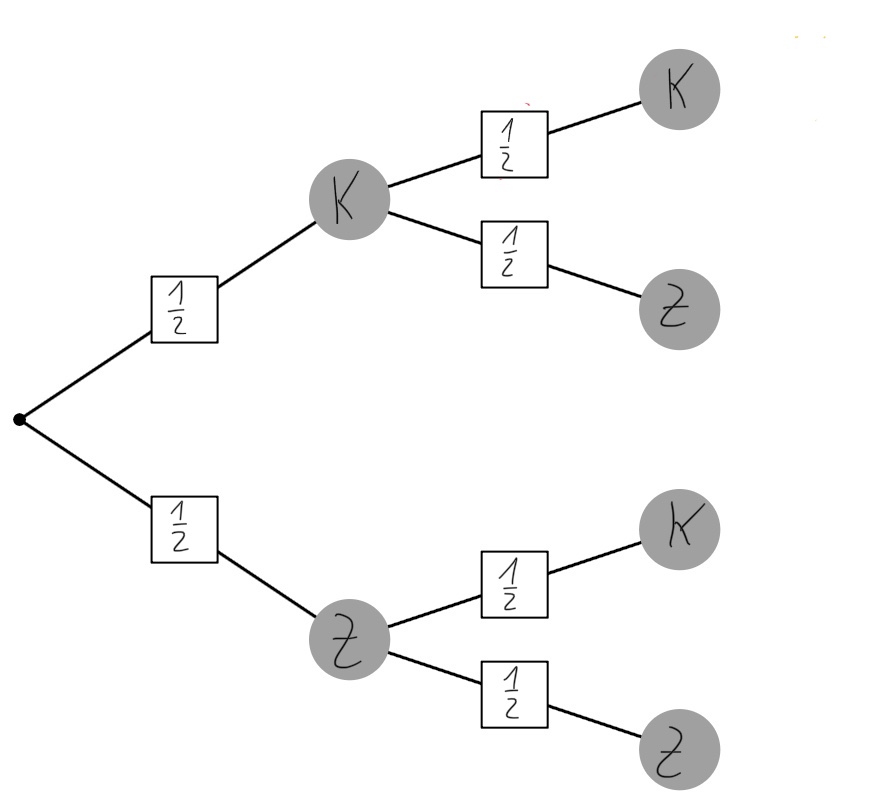
Es wird eine Münze zweimal geworfen. Mögliche Ergebnisse pro Wurf sind Kopf (K) und Zahl (Z).
Baumdiagramm und Wahrscheinlichkeiten der Stufen:
Wie bei einstufigen Laplace- Zufallsversuchen, ist auch hier die Wahrscheinlichkeit für ein Ereignis:

Am Beispiel des zweifachen Münzwurfes wäre das für das Ereignis "Nach jedem Wurf zeigt die Münze Zahl":
P(Z,Z) =  , weil nur ein Ergebnis auf das Ereignis zutrifft und es insgesamt vier Ergebnisse gibt.
, weil nur ein Ergebnis auf das Ereignis zutrifft und es insgesamt vier Ergebnisse gibt.
Übung
Seite 186,
Nr.3-4
Nr.5 a)-c)
Tipps für die Aufgaben im Buch:
Aufgabe 4:
(1) Differenz ist das Ergebnis eine Subtraktion. Die Differenz von 8 und 3 ist 5.
(2) Die Summe ist das Ergebnis einer Addition. Die Summe von 1 und 3 ist 4.
(4) Das Produkt ist das Ergebnis eine Multiplikation. Das Produkt von 2 und 3 ist 6.
(5) Die Vielfachen von 3 sind 3,6,9,12,15,..., Die Vielfachen von 3 berechnest du, indem du eine ganze Zahl mit 3 multiplizierst.
Lösungen für die Aufgaben im Buch:
a) Für das Baumdiagramm gibt es keine Lösung.
b) (1) 1/12
(2) 1/4
1);(5
}}
a) Für das Baumdiagramm gibt es keine Lösung
S = {(RR); (RG); (RS); (GR); (GG); (GS); (SR); (SG); (SS)}
b) 1/9
c)
P(E1) = 1/3
P(E2) = 4/9
P(E3) = 2/9
P(E4) = 5/9