Herta-Lebenstein-Realschule/Die Scheitelpunktform quadratischer Funktionen sportlich erarbeiten

Lernpfad Scheitelpunktform quadratische Funktionen sportlich erarbeiten
[[Bild: Bild von Hebi B. auf Pixabay |250px]]	Die Parameter a, d und e der Scheitelpunktform quadratische Funktionen f(x) = a (x + d)² + e werden mithilfe dreier "Sportler" erarbeiten

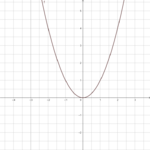
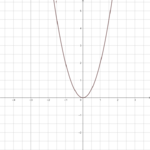
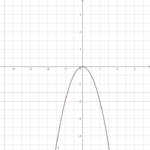
1. Anton: f(x) = ax²

Anton ist sehr sportlich, er spielt Basketball:

• 

  normal

• 

  gestreckt

• 

  gestaucht

Bedeutung des Parameters a

Welche Rolle spielt anton für den Graphen der Parabel?

Öffne die Seite und verändere a.

Welche Auswirkungen hat der anton auf das Schaubild der Normalparabel?

Bedeutung des Parameters a

Schreibe den Lückentext in dein Heft ab.

Wende dein Wissen an.

Ordne den Funktionsgraphen die passenden Funktionsgleichungen zu.

f(x) = x2	f(x) = - x2	f(x) = 0,5x2	f(x) = -0,5x2	f(x) = 2x2	f(x) = -2x2

y = x2 + 3	y = - x2 + 3	y = - x + 3	y = -x2 - 3	y = x - 3	y = x2 - 3

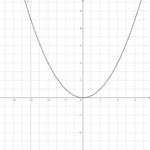
2. Detlef: f(x) = (x + d)²

Detlef ist ebenfalls sportlich, allerdings auch ein wenig dusselig. Er läuft beim Sprint immer in die entgegengesetzte Richtung.

• 

  Bild von OpenClipart-Vectors auf Pixabay

• 
• 
• 

  Detlef

Bedeutung des Parameters d

Welche Rolle spielt detlef ?

Öffne die Seite und verändere d.

Welche Auswirkungen hat detlf auf das Schaubild der Normalparabel?

Bedeutung des Parameters d

Schreibe den ausgefüllten Lückentext zur Bedeutung des Parameters d für in dein Heft ab.

Wende dein Wissen an

Ordne den Funktionsgraphen die passenden Funktionsgleichungen zu.

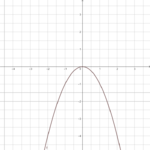
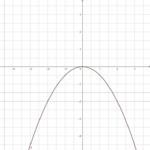
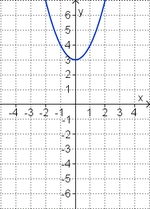
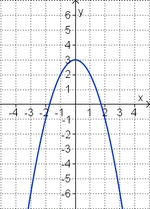
3. Emil: f(x) = x² + e

emil ist ebenfalls sehr sportlich:

Er kann sehr hoch springen, ebenso gut kann er tauchen.

Bedeutung des Parameters e

Welche Rolle spielt emil ?

Öffne die Seite und verändere e.

Welche Auswirkungen hat emil auf das Schaubild der Normalparabel?

Bedeutung des Parameters e

Schreibe den ausgefüllten Lückentext zur Bedeutung des Parameters e für in dein Heft ab.

Wende dein Wissen an

Ordne den Funktionsgraphen die passenden Funktionsgleichungen zu.