Geometrie im Dreieck/Auf den Spuren der Winkel: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 43: | Zeile 43: | ||
}} | }} | ||
{{Box|Merksatz: Wechselwinkel|{{Lösung versteckt|1=An zwei parallelen Geraden, die von einer weiterer Geraden geschnitten werden, erhält man '''Wechselwinkel''', indem man erst den Stufenwinkel und anschließend davon den Scheitelwinkel nimmt. Auch für Wechselwinkel gilt, dass sie gleich groß sind. | {{Box|Merksatz: Wechselwinkel|{{Lösung versteckt|1=[[Datei:Wechselwinkel.jpg|rechts|200x200px]] | ||
An zwei parallelen Geraden, die von einer weiterer Geraden geschnitten werden, erhält man '''Wechselwinkel''', indem man erst den Stufenwinkel und anschließend davon den Scheitelwinkel nimmt. Auch für Wechselwinkel gilt, dass sie gleich groß sind. | |||
In der Abbildung: α und β sind Wechselwinkel und es gilt α<math>=</math> β.|2=Merksatz|3=Merksatz verbergen}}|Merksatz | In der Abbildung: α und β sind Wechselwinkel und es gilt α<math>=</math> β.|2=Merksatz|3=Merksatz verbergen}}|Merksatz | ||
| Zeile 145: | Zeile 147: | ||
==Aufgabe 3: Wer bin ich? == | ==Aufgabe 3: Wer bin ich?== | ||
===Winkeltyp 1=== | ===Winkeltyp 1=== | ||
Mein Nachbarwinkel und ich bilden gemeinsam eine gestreckte Linie. Wir ergänzen und immer zu einem Halbkreis. Wer bin ich? | Mein Nachbarwinkel und ich bilden gemeinsam eine gestreckte Linie. Wir ergänzen und immer zu einem Halbkreis. Wer bin ich? | ||
| Zeile 152: | Zeile 154: | ||
{{Lösung versteckt|1=Ich bin der Nebenwinkel.|2=Lösung|3=Lösung}} | {{Lösung versteckt|1=Ich bin der Nebenwinkel.|2=Lösung|3=Lösung}} | ||
===Winkeltyp 2=== | === Winkeltyp 2=== | ||
Mein Partner und ich sind stets auf der gleichen Seite, obwohl wir auf unterschiedlichen Geraden (parallel zueinander) schwimmen. Wer bin ich? | Mein Partner und ich sind stets auf der gleichen Seite, obwohl wir auf unterschiedlichen Geraden (parallel zueinander) schwimmen. Wer bin ich? | ||
{{Lösung versteckt|1=Ich entstehe, wenn eine dritte Gerade zwei parallele Linien schneidet.|2=Tipp 1|3=Tipp 1}} | {{Lösung versteckt|1=Ich entstehe, wenn eine dritte Gerade zwei parallele Linien schneidet.|2=Tipp 1|3=Tipp 1}} | ||
| Zeile 170: | Zeile 172: | ||
{{Lösung versteckt|1=Ich bin der Scheitelwinkel.|2=Lösung|3=Lösung}} | {{Lösung versteckt|1=Ich bin der Scheitelwinkel.|2=Lösung|3=Lösung}} | ||
==Aufgabe 4: Winkel in der Sporthalle== | ==Aufgabe 4: Winkel in der Sporthalle == | ||
=== Zeichnen=== | ===Zeichnen=== | ||
{{Box|Aufgabe 4.1.|Zeichne die Sprossenwand, die Bänke, den großen Kasten und die Linie (auf dem Boden) als Geraden in dein Heft. Übertrage außerdem die Winkel aus dem Foto in deine Zeichnung. (z.B. zwischen Bank und Sprossenwand). | {{Box|Aufgabe 4.1.|Zeichne die Sprossenwand, die Bänke, den großen Kasten und die Linie (auf dem Boden) als Geraden in dein Heft. Übertrage außerdem die Winkel aus dem Foto in deine Zeichnung. (z.B. zwischen Bank und Sprossenwand). | ||
| Zeile 184: | Zeile 186: | ||
}} | }} | ||
===Winkel benennen und berechnen=== | === Winkel benennen und berechnen=== | ||
{{Box|Aufgabe 4.2.|Benenne die Winkeltypen, die in der Darstellung auftauchen und berechne deren Größe. | {{Box|Aufgabe 4.2.|Benenne die Winkeltypen, die in der Darstellung auftauchen und berechne deren Größe. | ||
Version vom 7. November 2024, 16:42 Uhr
Kapitel-Informationskästchen
Aufgabe 1: Zuordnungen von Begriffen zu Abbildungen
Teste dein Wissen zu den verschiedenen Winkelarten. Ordne die Bilder der Winkel den richtigen Bezeichnungen zu.
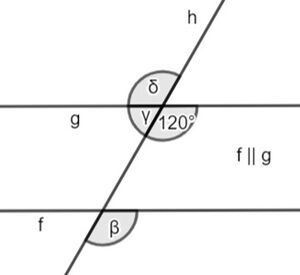
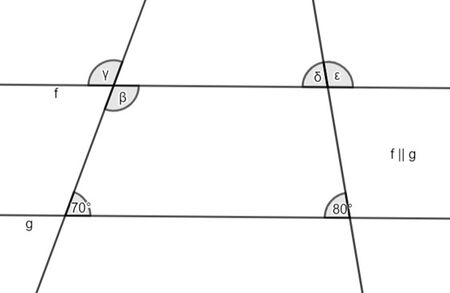
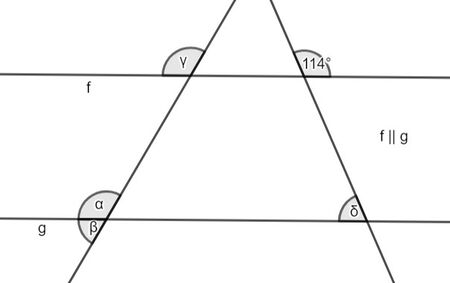
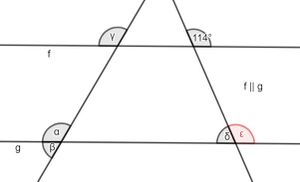
Aufgabe 2: Winkelgrößen bestimmen
Schwierigkeitsstufe I
Schwierigkeitsstufe II
Schwierigkeitsstufe III
Aufgabe 3: Wer bin ich?
Winkeltyp 1
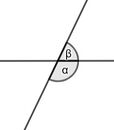
Mein Nachbarwinkel und ich bilden gemeinsam eine gestreckte Linie. Wir ergänzen und immer zu einem Halbkreis. Wer bin ich?
Je größer mein Nachbarwinkel ist, desto kleiner bin ich.
Mein Nachbarwinkel und ich ergeben gemeinsam 180 Grad. Wenn er beispielsweise 70 Grad aufweist, besitze ich 110 Grad.
Ich bin der Nebenwinkel.
Winkeltyp 2
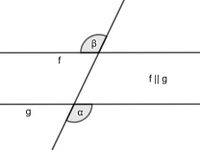
Mein Partner und ich sind stets auf der gleichen Seite, obwohl wir auf unterschiedlichen Geraden (parallel zueinander) schwimmen. Wer bin ich?
Ich entstehe, wenn eine dritte Gerade zwei parallele Linien schneidet.
Mein Partner und ich haben die gleiche Winkelgröße.
Ich bin der Stufenwinkel.
Winkeltyp 3
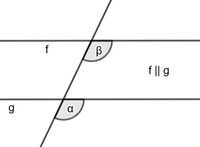
Mein Partner und ich sind nie auf der gleichen Seite. Vielleicht liegt es daran, dass wir stets auf einer unterschiedlichen Geraden schwimmen. Wer bin ich?
Ich entstehe, wenn eine dritte Gerade zwei parallele Linien schneidet.
Mein Partner und ich haben die gleiche Winkelgröße.
Ich bin der Wechselwinkel.
Winkeltyp 4
Mein Partner und ich sind uns sehr ähnlich - wir haben immer die gleiche Winkelgröße. Wer bin ich?
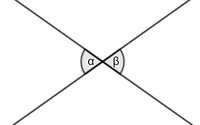
Mein Partner und ich haben denselben Schnittpunkt der Geraden.
Wir liegen zwar nich nebeneinander, dafür aber direkt gegenüber.
Ich bin der Scheitelwinkel.