Gymnasium Marktbreit/Wissenschaftswoche 2024/11bMatheInfo/Beispiele Logistisches Wachstum: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
(Die Seite wurde neu angelegt: „In einem Internat leben 500 Menschen, einer davon infiziert sich Covid-19, nach einer Wochen sind bereits 100 Menschen angesteckt.<ref>Idee: LogistischesWachstumAufgaben.pdf (groolfs.de), Aufgabe 2</ref> a) Bestimmen Sie den Funktionsterm. b) Nach welcher Zeit sind 80% der Bewohner erkrankt? c) Wie viele Bewohner erkranken in den ersten Tagen pro Stunde? Lösung: a) <math>K(x)={K \over N_0 + (K-N_0\cdot e^{-K\cdot k \cdot x}) }</math> <math>100={500…“) Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung |
||
| Zeile 40: | Zeile 40: | ||
<math>\log_{e} ({1\over 1996})= -0,7x</math> | <math>\log_{e} ({1\over 1996})= -0,7x</math> | ||
<math>-7,6= -0,7x\mid\div-0,7</math> | <math>-7,6= -0,7x\mid\div(-0,7)</math> | ||
<math>x=10,9</math> | <math>x=10,9</math> | ||
Nach 10,9 Tagen sind 80% infiziert. | Nach 10,9 Tagen sind 80% infiziert. | ||
c) | c) | ||
Version vom 5. Juli 2024, 06:39 Uhr
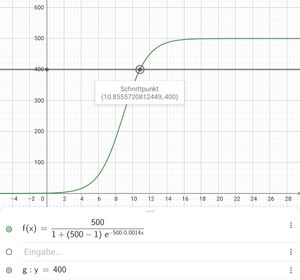
In einem Internat leben 500 Menschen, einer davon infiziert sich Covid-19, nach einer Wochen sind bereits 100 Menschen angesteckt.[1]
a) Bestimmen Sie den Funktionsterm.
b) Nach welcher Zeit sind 80% der Bewohner erkrankt?
c) Wie viele Bewohner erkranken in den ersten Tagen pro Stunde?
Lösung:
a)
b)
Nach 10,9 Tagen sind 80% infiziert.
c)
Pro Tag erkranken 4,1 Menschen
- ↑ Idee: LogistischesWachstumAufgaben.pdf (groolfs.de), Aufgabe 2