Benutzer:Gabriel.cicek/Zufällige Ereignisse und ihre Wahrscheinlichkeit/Berechnen relativer Häufigkeiten mit Baumdiagrammen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 3: | Zeile 3: | ||
<big>Beispiel: | <big>Beispiel: | ||
</big> | </big> | ||
<big>Immer mehr Menschen die Arbeiten haben einen Teilzeitjob. Vor allem Frauen arbeiten häufig in Teilzeit. Eine Befragung ergab das nebenstehende Baumdiagramm.</big> | <big>Immer mehr Menschen die Arbeiten haben einen Teilzeitjob. Vor allem Frauen arbeiten häufig in Teilzeit. Eine Befragung ergab das nebenstehende Baumdiagramm.</big> | ||
Version vom 20. September 2023, 09:34 Uhr
Beispiel:
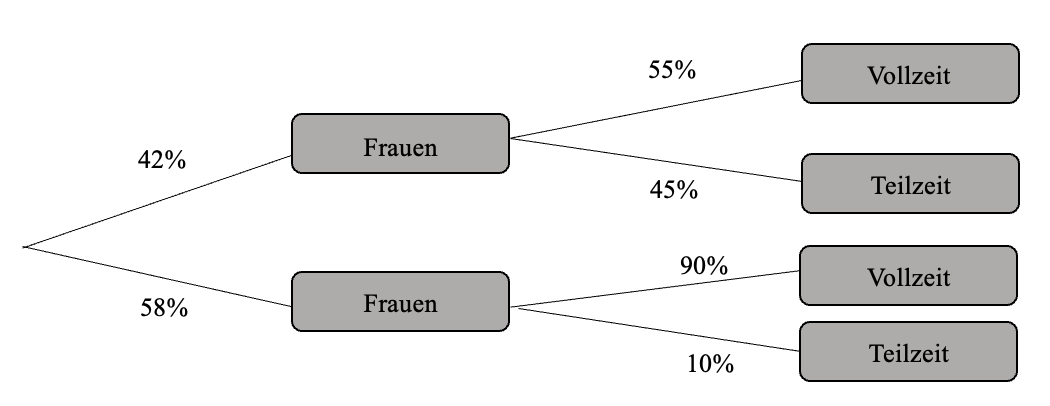
Immer mehr Menschen die Arbeiten haben einen Teilzeitjob. Vor allem Frauen arbeiten häufig in Teilzeit. Eine Befragung ergab das nebenstehende Baumdiagramm.
So liest du das Baumdiagramm:
42% der befragten sind Frauen.
58% der befragten sind Männer.
55% der befragten Frauen arbeiten in Vollzeit.
45% der befragten Frauen arbeiten Teilzeit.
90% der befragten Männer arbeiten in Vollzeit.
10% der befragten Männer arbeiten in Teilzeit.
Aufgabe:
E:Wie viel % aller Befragten arbeiten in Vollzeit?
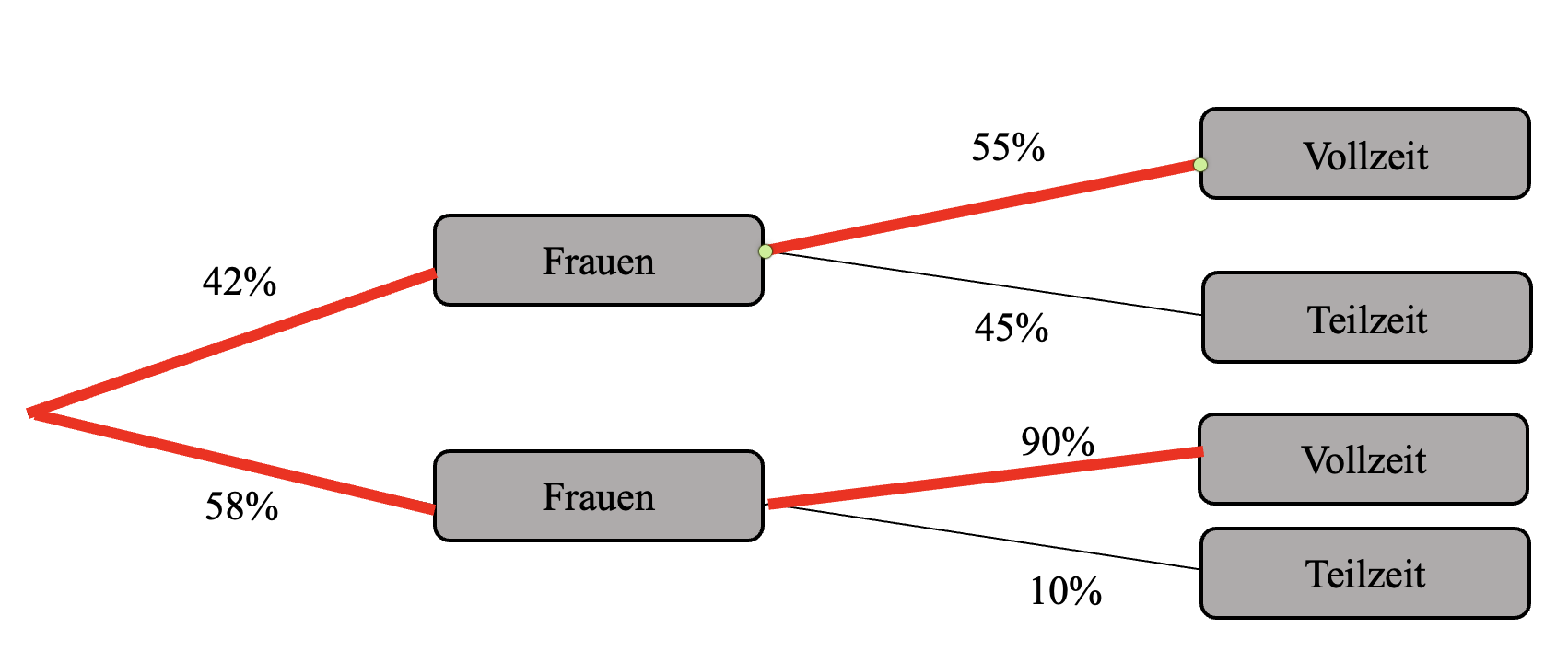
Um die relative Häufigkeit auszurechnen, musst du dir überlegen, welche Ergebnisse (Pfade) auf dein Ereignis passen. Anschließend wendest du wie gewohnt die Produkt- und Summenregel an.
Wie du siehst passende die Ergebnisse (Frauen,Vollzeit) und (Männer, Vollzeit)
Zuerst wenden wir die Produktregel an:
P(Frauen, Vollzeit) = 0,42 ⋅ 0,55 = 0,231 = 23,1%
P(Männer, Vollzeit) = 0,58 ⋅ 0,9 = 0,522 = 52,2%
Jetzt wenden wir die Summenregel an:
P(E) = P(Frauen,Vollzeit) ⋅P(Männer, Vollzeit) = 23,1% + 52,2% = 75,3%
Antwort: 75,3% aller Befragten arbeiten in Vollzeit.