Benutzer:Gabriel.cicek/Zufällige Ereignisse und ihre Wahrscheinlichkeit/6.Pfadregeln zur Berechnung von Wahrscheinlichkeiten: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 34: | Zeile 34: | ||
Um die Wahrscheinlichkeit eines Ereignisses zu berechnen, werden die einzelnen Wahrscheinlichkeiten der günstigen Ergebnisse '''addiert'''.<br> | Um die Wahrscheinlichkeit eines Ereignisses zu berechnen, werden die einzelnen Wahrscheinlichkeiten der günstigen Ergebnisse '''addiert'''.<br> | ||
{{Box|Summenregel|Die Wahrscheinlichkeit eines Ereignisses wird berechnet, indem die Wahrscheinlichkeiten von allen günstigen Ergebnissen, die zu diesem Ereignis gehören, '''addiert''' werden.|Arbeitsmethode}} | |||
Beispiel:<br> | Beispiel:<br> | ||
E: "Die Münze zeigt mindestens einmal Zahl"<br> | E: "Die Münze zeigt mindestens einmal Zahl"<br> | ||
Version vom 13. September 2023, 13:38 Uhr
Wie berechne ich Wahrscheinlichkeiten (mithilfe eines Baumdiagramms)?
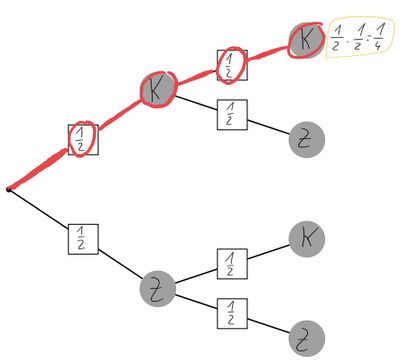
Um zu einem möglichen Ergebnis zu gelangen, musst du einen bestimmten Pfad des Baumdiagrammes gehen. Die Wahrscheinlichkeit dieses Ergebnisses berechnest du, indem du die Wahrscheinlichkeiten entlang des Pfades multiplizierst.
Beispiel:
Es wird eine Münze zweimal geworfen. Mögliche Ergebnisse pro Wurf sind Kopf (K) und Zahl (Z). Die Wahrscheinlichkeit für das Ergebnis Kopf,Kopf lässt sich mit der Produktregel wie folgt berechnen:
P(K,K) = ∙ = = 0,25 = 25%
Baumdiagramm:
Falls du noch zusätzliche Hilfe zur Produktregel brauchst benötigst, findest du hier ein Erklärvideo.
Schaue es nur, wenn du es nicht verstanden hast!!!
Nun betrachten wir nicht mehr nur einzelne Ergebnisse sondern berechnen die Wahrscheinlichkeiten von Ereignissen.
Ein Ereignis setzt sich aus mehreren günstigen Ergebnissen zusammen.
Beispiel:
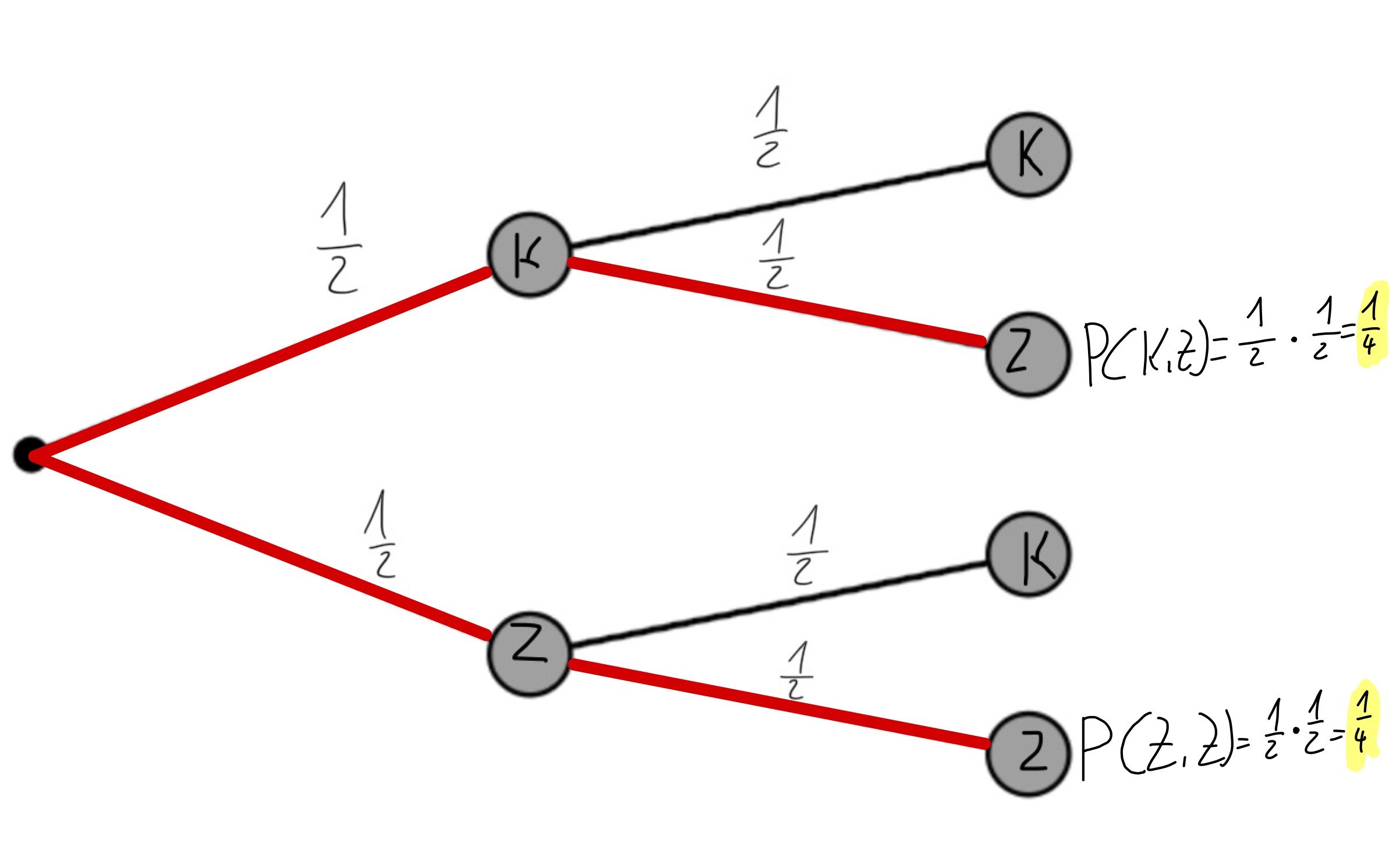
Das Ereignis E: Die Münze zeigt mindestens einmal Zahl" setzt sich aus den Ergebnissen (K,Z) und (Z,Z) zusammen.
Um die Wahrscheinlichkeit eines Ereignisses zu berechnen, werden die einzelnen Wahrscheinlichkeiten der günstigen Ergebnisse addiert.
Beispiel:
E: "Die Münze zeigt mindestens einmal Zahl"
P(E) = P(K,Z) + P(Z,Z)
= +
= = 0,125 = 12,5%
Baumdiagramm:
Falls du noch zusätzliche Hilfe zur Summenregel brauchst benötigst, findest du hier ein Erklärvideo.
Schaue es nur, wenn du es nicht verstanden hast!!!