Benutzer:Gabriel.cicek/Zufällige Ereignisse und ihre Wahrscheinlichkeit/Wahrscheinlichkeit bei mehrstufigen Laplace-Versuchen

Merke

Sind bei einem mehrstufigen Zufallsversuch die Wahrscheinlichkeiten auf jeder Stufe gleich groß, so ist der Versuch ein mehrstufiger Laplace-Versuch.

Beispiel:
Es wird eine Münze zweimal geworfen. Mögliche Ergebnisse pro Wurf sind Kopf (K) und Zahl (Z).

Baumdiagramm und Wahrscheinlichkeiten der Stufen:

Wie bei einstufigen Laplace- Zufallsversuchen, ist auch hier die Wahrscheinlichkeit für ein Ereignis:

$P(A) = \frac{\text{Anzahl der günstigen} \text{ Ergebnisse}}{\mathrm{Anzahl\ aller\ m\ddot oglichen\ Ergebnisse}}$

Am Beispiel des zweifachen Münzwurfes wäre das für das Ereignis "Nach jedem Wurf zeigt die Münze Zahl":

P(Z,Z) = $\tfrac{1}{4}$, weil nur ein Ergebnis auf das Ereignis zutrifft und es insgesamt vier Ergebnisse gibt.

Übung

Seite 186, Nr.3-5

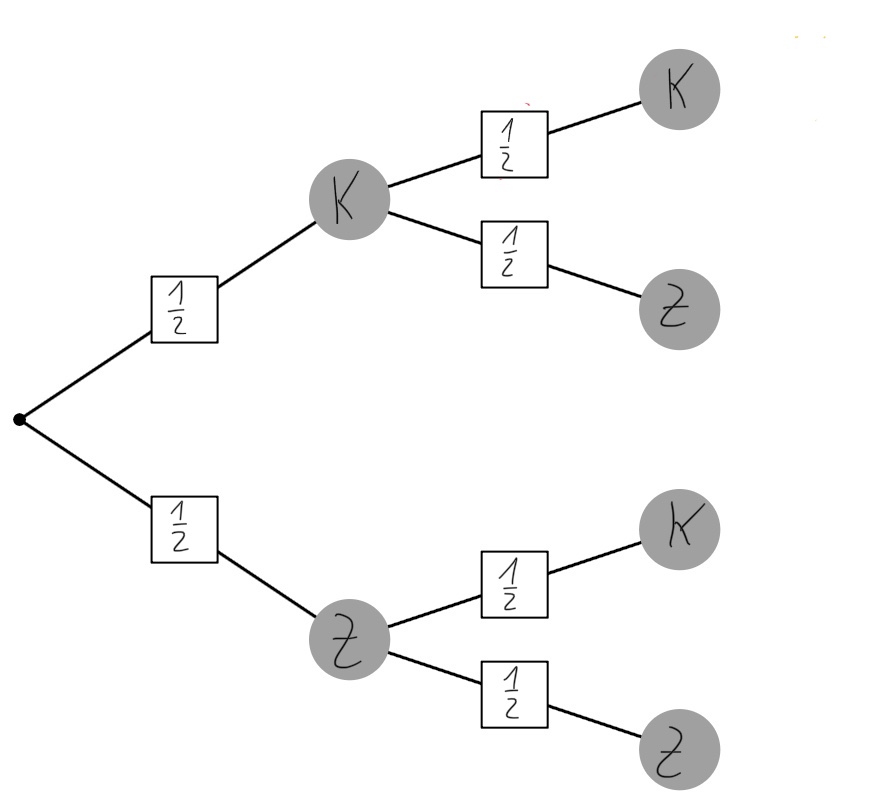
a) Für das Baumdiagramm gibt es keine Lösung. b) (1) 1/12

(2) 1/4

Die Differenz der Augenzahlen ist größer als 2:

Günstige Wurfkombinationen: (3,1), (4,1), (4,2), (5,1), (5,2), (5,3), (6,1), (6,2), (6,3), (6,4)

Anzahl der günstigen Kombinationen: 10

Wahrscheinlichkeit: 10/36 = 5/18

Die Summe der Augenzahlen beträgt 8:

Günstige Wurfkombinationen: (2,6), (3,5), (4,4), (5,3), (6,2)

Anzahl der günstigen Kombinationen: 5

Wahrscheinlichkeit: 5/36

Die Summe der Augenzahlen ist kleiner als 5:

Günstige Wurfkombinationen: (1,1), (1,2), (2,1), (1,3), (2,2), (3,1)

Anzahl der günstigen Kombinationen: 6

Wahrscheinlichkeit: 6/36 = 1/6

Das Produkt der Augenzahlen beträgt 6:

Günstige Wurfkombinationen: (1,6), (2,3), (3,2), (6,1)

Anzahl der günstigen Kombinationen: 4

Wahrscheinlichkeit: 4/36 = 1/9

Die Summe der Augenzahlen ist ein Vielfaches von 3:

Günstige Wurfkombinationen: (3,3), (6,6), (1,2), (2,1), (2,4), (4,2), (3,6), (6,3)

Anzahl der günstigen Kombinationen: 8

Wahrscheinlichkeit: 8/36 = 2/9

Das Produkt der Augenzahlen ist durch 4 teilbar:

Günstige Wurfkombinationen: (1,4), (2,4), (4,1), (4,2)

Anzahl der günstigen Kombinationen: 4

Wahrscheinlichkeit: 4/36 = 1/9