C.Schroer/Terme addieren und subtrahieren: Unterschied zwischen den Versionen
(Lösungshinweise gelöscht) |
Keine Bearbeitungszusammenfassung |
||
| Zeile 77: | Zeile 77: | ||
d) 0,5c∙3d²∙6c = 0,5∙3∙6∙c∙c∙d² = 9c²d² | d) 0,5c∙3d²∙6c = 0,5∙3∙6∙c∙c∙d² = 9c²d² | ||
e) 6ab:3b = <math>\tfrac{6\cdot a\cdot b}{3 \cdot b}</math> = 2∙a (gekürzt) | e) 6ab:3b = <math>\tfrac{6\cdot a\cdot b}{3 \cdot b}</math> = 2∙a (gekürzt)<br /> {{#ev:youtube|ghBckXYjfrs|800|center}} | ||
<br />{{#ev:youtube|ghBckXYjfrs|800|center}} | |||
Version vom 27. August 2023, 11:55 Uhr
Dieser Lernpfad wurde im Original erstellt von Frau Buß-Haskert (Herta-Lebenstein-Realschule) und wurde veröffentlicht unter der Lizenz CC BY SA. Herzlichen Dank!
2) Terme vereinfachen
2.1 Terme addieren und subtrahieren
Übertrage den Merksatz und die nachfolgenden Beispiele in dein Heft (Zeichnungen und Rechnungen):
Begründung (zeichnerisch):
x+x+x = 3x
x+y+x+y+x = x+x+x+y+y = 3x + 2y
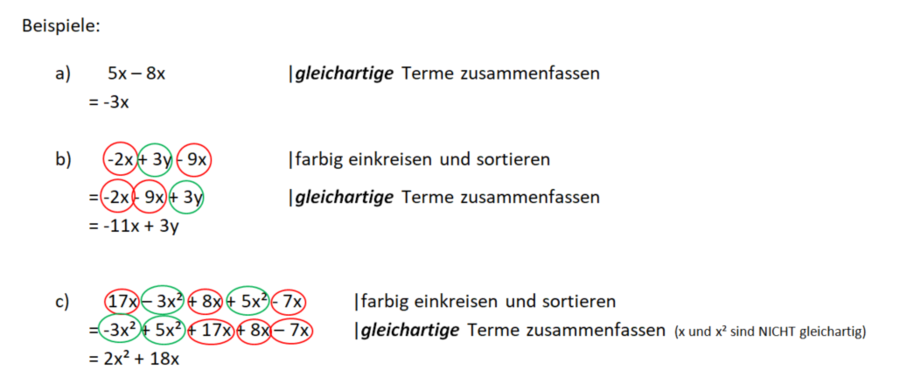
Vorsicht: x, x² und x³ können NICHT zusammengefasst werden, denn sie sind nicht gleichartig!
Zusätzliche Übungsmöglichkeiten findest du in den Learningapps:
Teste dich - Terme addieren und subtrahieren
2.2 Terme multiplizieren und dividieren
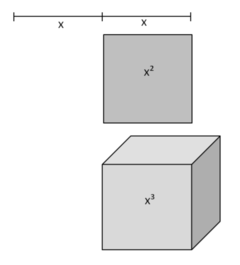
Die Giraffen im Zoo sollen ein neues Außengehege bekommen. Dies soll 6-mal so lang und 4-mal so breit werden wie das Giraffenhaus.
Welche Fläche steht den Giraffen dann außen zur Verfügung?
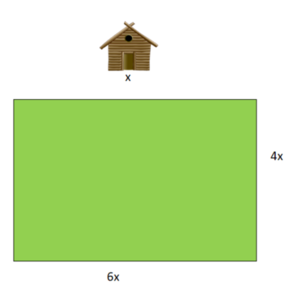
Länge des Rechtecks: 6x
Breite des Rechtecks: 4x
A = 6∙x ∙ 4∙x |sortiere, vertausche die Reihenfolge der Faktoren
= 6∙4∙x∙x |fasse zusammen
= 24x²
Übertrage den Merksatz und die nachfolgenden Beispiele in dein Heft.
Beispiele:
a) a∙a = a²
b) 4b∙0,2b = 4∙0,2∙b∙b = 0,8b²
c) 12x∙7y = 12∙7∙x∙y = 84xy
d) 0,5c∙3d²∙6c = 0,5∙3∙6∙c∙c∙d² = 9c²d²
e) 6ab:3b = = 2∙a (gekürzt)
Teste dich - Terme multiplizieren und dividieren
2.3 Vermischte Übungen
Nun folgen Übungen, bei denen du entscheiden musst, ob Terme addiert/subtrahiert oder multipliziert/dividiert werden. Lies noch einmal die Merksätze auf dieser Seite. Sortiere in der nachfolgenden LearningApp passend.
Unterscheide zwischen den Rechenarten Strichrechung und Punktrechnung! Das Zusammenfassen der Terme ist unterschiedlich!
a) 5+5 = 10 aber 5∙5 = 25
a) a + 2a = 3a Das "hoch 2" bei a ist falsch, denn die Terme werden addiert, also dürfen gleichartige Terme zusammengefasst werden und die Terme a und 2a sind gleichartig, die Variable a bleibt unverändert.
x + x² kann nicht weiter zusammengefast werden, denn die Terme werde addiert, also dürfen nur gleichartige Terme zusammengefasst werden, x und x² sind nicht gleichartig.
c) vgl. b)
d) n²∙2n = 2n³ Die Terme werden multipliziert, daher werden die Zahlen und Variablen getrennt mutlipliziert und die Variablen werden zu Potenzen zusammengefasst, also
n²∙2n = 2∙n²∙n = 2n³
e) 2z² + 2z² = 4z² Die Terme werden addiert, die Terme sind gleichartig und dürfen zusammengefasst werden. Dabei bleibt die Variable z² gleich.
Die Terme werden jeweils addiert, also dürfen gleichartige Terme zusammengefasst werden. Die Terme sind gleichartig, sie heißen nun z.B. "cd" statt nur "c".
Die Terme werden jeweils addiert bzw. subtrahiert, es dürfen also gleichartige Terme zusammengefasst werden.
= 5ab - ab + 3mn + 2mn
= 4ba + 5mn