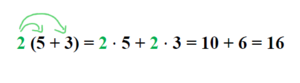Jule Volbers/Testseite: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 597: | Zeile 597: | ||
{{Lösung versteckt|1=Nutze den Satz des Pythagoras. Fertige hierzu eine Skizze an.|2=Tipp 2|3=Tipp ausblenden}} | {{Lösung versteckt|1=Nutze den Satz des Pythagoras. Fertige hierzu eine Skizze an.|2=Tipp 2|3=Tipp ausblenden}} | ||
{{Lösung versteckt|1=x: Länge der kürzeren Kathete. Dann ist (x+1) die Länge der längeren Kathete.<br> Nach dem Satz des Pythagoras gilt: | {{Lösung versteckt|1=x: Länge der kürzeren Kathete. Dann ist (x+1) die Länge der längeren Kathete.<br> Nach dem Satz des Pythagoras gilt: | ||
<math>\begin{array}{lcl} x^2 + (x+1)^2 & = & 25 \\\Leftrightarrow x^2+x^2+2x+1 & = & 25\\\Leftrightarrow 2x^2+2x+1 & = & 25\mid-25 \\\Leftrightarrow 2x^2+2x-24 & = & 0\mid : 2\\\Leftrightarrow x^2+x - 12 & = & 0\mid pq-Formel \\\Leftrightarrow x & = & -0,5+3,5 \lor x & = & -0,5-3,5\\\Leftrightarrow x & = & 3 \lor x & = & -4 \end{array}</math> | |||
<math>\begin{array}{lcl} x^2+(x+1)^2 & = & 25 \\\Leftrightarrow x^2 + x^2+2x+1 & = & 25\\\Leftrightarrow 2x^2 +2x+1 & = & 25 \mid -24 \\\Leftrightarrow x^2 + x -24 24 & = & 0 \: 2\\\Leftrightarrow x^2+x-12 & = & 0 \\\Leftrightarrow 24 & = & 2x\mid: 2\\\Leftrightarrow 12 & = & x \end{array}</math> | <math>\begin{array}{lcl} x^2+(x+1)^2 & = & 25 \\\Leftrightarrow x^2 + x^2+2x+1 & = & 25\\\Leftrightarrow 2x^2 +2x+1 & = & 25 \mid -24 \\\Leftrightarrow x^2 + x -24 24 & = & 0 \: 2\\\Leftrightarrow x^2+x-12 & = & 0 \\\Leftrightarrow 24 & = & 2x\mid: 2\\\Leftrightarrow 12 & = & x \end{array}</math> | ||
|2=Lösung |3= Lösung ausblenden}} | |2=Lösung |3= Lösung ausblenden}} | ||
|3 = Üben|Farbe={{Farbe|orange|heller}}}} | |3 = Üben|Farbe={{Farbe|orange|heller}}}} | ||
Version vom 23. März 2023, 10:32 Uhr
Willkommen auf dem Lernpfad: Nützliche Werkzeuge - Variablen, Terme und Gleichungen.
Kaum tauchen Buchstaben auf, wird Mathe für manche kompliziert. Dabei sind Variablen, Terme und Gleichungen sehr nützliche ud häufig benötigte Werkzeuge, die man sicher nutzen können sollte. In diesem Kapitel geht es darum, grundlegende Begriffe und Verfahren zum Aufstellen und Umformen von Termen sowie dem Lösen von Gleichungen zu wiederholen. Im Anschluss findest kannst du dein Wissen in Anwendungsaufgaben testen.
.
1.Terme, Variablen und Gleichungen
2.Terme
Terme aufstellen
Terme vereinfachen
a) =
b) =
c) =
d) =
e) =
f)
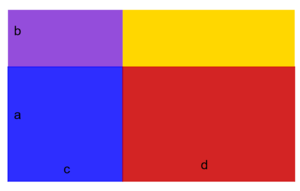
Klammern in Termen
3. Gleichungen
4. Aufgaben zum Trainieren
Zahlenrätsel
Geometrische Anwendungen