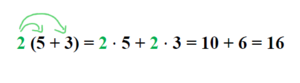Jule Volbers/Testseite: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 108: | Zeile 108: | ||
<math>(b+c){\color{green}a} = b{\color{green}a} + {\color{green}a} </math>.<br/> | <math>(b+c){\color{green}a} = b{\color{green}a} + {\color{green}a} </math>.<br/> | ||
Formuliere die Regel in eigenen Worten. Wende sie auf das Beispiel a = 2, b = 5 und c = 3 an. Kontrolliere dann deine Lösung. | Formuliere die Regel in eigenen Worten. Wende sie auf das Beispiel a = 2, b = 5 und c = 3 an. Kontrolliere dann deine Lösung. | ||
{{Lösung versteckt|1= Man multipliziert einen <span style="color: green">'''Faktor'''</span> mit einer Klammer, indem man den Faktor mit jedem einzelnen Glied in der Klammer multipliziert. | {{Lösung versteckt|1= Der Flächeninhalt des blauen Rechtecks ist <math> a\cdotb = ab [FE]</math> , der des roten Rechtecks <math> a\cdot c = ab [FE]</math>. Die beiden Rechtecks bilden ein großes Rechteck mit den Seitenlängen a [LE] und (b+c) [LE]. Der Flächeninhalts dieses Rechtecks kann auf 2 Arten berechnet werden: A<sub>groß</sub> = <math> a\cdot (b+c) = a(b+c) [FE]</math> oder durch Addition der beiden Flächeninhalte der kleinen Rechtecke: <math> ab [FE] + ac [FE]</math>. Dies ist die Erklärung der ersten Gleichung. Da die Multiplikation kommutativ ist (z.B. ist ab = ba), gilt auch die 2. Gleichung. | ||
Formulierung in eigenen Worten: Durch Man multipliziert einen <span style="color: green">'''Faktor'''</span> mit einer Klammer, indem man den Faktor mit jedem einzelnen Glied in der Klammer multipliziert. | |||
[[Datei:Ausmultiplizieren 1.png|mini | links | thumb ]] | [[Datei:Ausmultiplizieren 1.png|mini | links | thumb ]] | ||
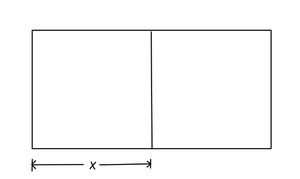
Es spielt keine Rolle, ob der Faktor links oder rechts von der Klammer steht: <br /> | Es spielt keine Rolle, ob der Faktor links oder rechts von der Klammer steht: <br /> | ||
| Zeile 125: | Zeile 126: | ||
[[Datei:Distr2.png|mini]] | [[Datei:Distr2.png|mini]] | ||
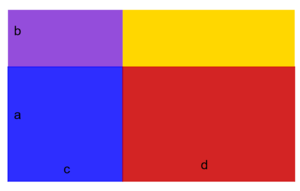
{{Lösung versteckt|1= Zwei Summen (oder Differenzen) werden miteinander multipliziert, indem man '''jeden Summanden der ersten Klammer mit jedem Summanden der zweiten Klammer multipliziert:''' | {{Lösung versteckt|1= Hier bilden die vier kleinen Rechtecke ein großes Rechteck. Die Flächeninhalte der einzelnen Rechtecke sind: | ||
<math> a\cdot c = ac [FE]</math> (blau), <math> b\cdot c = bc [FE]</math> (lila), <math> a\cdot d = ad [FE]</math> (rot), <math> b\cdot d = bd [FE]</math> (gelb). Auch hier bilden die kleinen Rechtecke ein großes Rechteck mit den Seitenlängen (a+b) [LE] und (c+d) [LE]. Der Flächeninhalt des großen Rechtecks lässt sich wieder auf zwei Arten berechnen: A<sub>groß</sub> = <math> (a+b)\cdot (c+d)) = (a+b)(c+d) [FE]</math> oder durch Addition der vier Flächeninhalte der kleinen Rechtecke: <math> ab [FE] + ad [FE] + bc [FE] + bd [FE ]</math>. | |||
Formulierung in eigenen Worten: Zwei Summen (oder Differenzen) werden miteinander multipliziert, indem man '''jeden Summanden der ersten Klammer mit jedem Summanden der zweiten Klammer multipliziert:''' | |||
[[Datei:Ausmultiplizieren 2.png|400px | links| thumb]] <br /> <br /> | [[Datei:Ausmultiplizieren 2.png|400px | links| thumb]] <br /> <br /> | ||
Es ist | Es ist | ||
Version vom 22. März 2023, 13:43 Uhr
Kaum tauchen Buchstaben auf, wird Mathe für manche kompliziert. Dabei sind Variablen, Terme und Gleichungen sehr nützliche ud häufig benötigte Werkzeuge, die man sicher nutzen können sollte. In diesem Kapitel geht es darum, grundlegende Begriffe und Verfahren zum Aufstellen und Umformen von Termen sowie dem Lösen von Gleichungen zu wiederholen. Im Anschluss findest kannst du dein Wissen in Anwendungsaufgaben testen.
.
1.Terme, Variablen und Gleichungen
2.Terme
Terme aufstellen
Terme vereinfachen
a) =
b) =
c) =
d) =
e) =
f)
Klammern in Termen
3. Gleichungen
4. Aufgaben zum Trainieren
Zahlenrätsel
Geometrische Anwendungen
Was ist gegeben?
zwei flächengleiche Flächen (Quadrat und Rechteck)
x = Seitenlänge der quadratischen Weide
x - 4 = eine Seitenlänge der rechteckigen Weide (3m kürzer)
x + 6 = andere Seitenlänge der rechteckigen Weide (5m länger)
Die beiden Weiden sind flächengleich, d.h. ihr Flächeninhalt ist gleich.
Benutze zum Aufstellen der Gleichung die Formeln für die Berechnung des Flächeninhaltes eines Quadrats und eines Rechtecks.
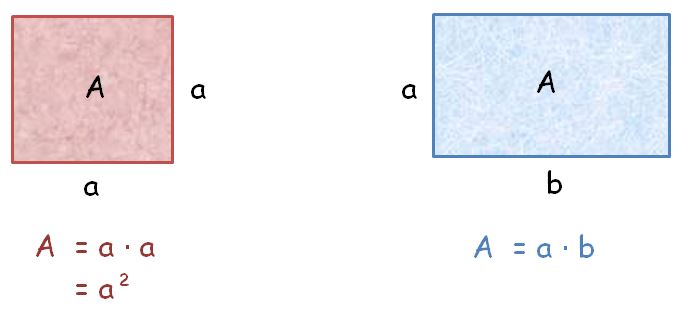
Beide Flächen sind gleich groß, daher lautet die Gleichung:
x² = (x – 4) (x + 6)
Versuche nun x zu berechnen. Löse hierfür zunächst die Klammern auf.Du hast nun herausgefunden, dass die Länge und Breite der quadratischen Weide je 12m beträgt. Damit kannst du jetzt die Seitenlängen der rechteckigen Weide berechnen. Setze hierfür x = 12 in deine aufgestellten Terme ein:
- x - 4 (eine Seitenlänge des Rechtecks)
- x + 6 (andere Seitenlänge des Rechtecks)