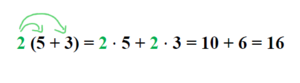Jule Volbers/Testseite: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 1: | Zeile 1: | ||
<div style="font-size: 14pt; background-color: #8B8386 ; text-align: center; color: white; padding: 5px 100px 5px 100px; margin-top: 5px; "> Willkommen auf dem Lernpfad: Nützliche Werkzeuge - Terme und Gleichungen. </div> | <div style="font-size: 14pt; background-color: #8B8386 ; text-align: center; color: white; padding: 5px 100px 5px 100px; margin-top: 5px; "> Willkommen auf dem Lernpfad: Nützliche Werkzeuge - Terme und Gleichungen. </div> | ||
[[Datei:Calcul mental.png| | [[Datei:Calcul mental.png|300 px|right]] | ||
In diesem Lernpfad geht es um das Vertiefen deines Wissens über '''Terme, Variablen und Gleichungen'''. | In diesem Lernpfad geht es um das Vertiefen deines Wissens über '''Terme, Variablen und Gleichungen'''. | ||
Du findest hier eine Wiederholung zu den Begriffen und Übungsaufgaben zu den Themen Terme aufstellen, Terme umformen und Gleichungen lösen. <s>.</s> | Du findest hier eine Wiederholung zu den Begriffen und Übungsaufgaben zu den Themen Terme aufstellen, Terme umformen und Gleichungen lösen. <s>.</s> | ||
<br/> | |||
=='''1.Terme, Variablen und Gleichungen'''== | =='''1.Terme, Variablen und Gleichungen'''== | ||
{{Box|1='''Was ist Was?" - Wiederhole die Begriffe!'''|2= Ergänze den Lückentext. Prüfe das Ergebnis und übertrage die Lösung in den Kasten zur Aufgabe in deinem Begleitmaterial. | {{Box|1='''Was ist Was?" - Wiederhole die Begriffe!'''|2= Ergänze den Lückentext. Prüfe das Ergebnis und übertrage die Lösung in den Kasten zur Aufgabe in deinem Begleitmaterial. | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
Variablen sind '''Zeichen''' (meistens kleine Buchstaben). Sie sind '''Platzhalter'''. Du kannst '''Zahlen''' für sie einsetzen. Terme sind '''Rechenausdrücke'''. Terme können Zahlen, Rechenzeichen, Klammern und '''Variable''' enthalten. Werden zwei '''Terme''' mit einem Gleichheitszeichen verbunden, entsteht eine '''Gleichung'''. Es gibt verschiedene Arten von Gleichungen. Wichtige Arten sind die '''linearen''' und die '''quadratischen''' Gleichungen. | Variablen sind '''Zeichen''' (meistens kleine Buchstaben). Sie sind '''Platzhalter'''. Du kannst '''Zahlen''' für sie einsetzen. Terme sind '''Rechenausdrücke'''. Terme können Zahlen, Rechenzeichen, Klammern und '''Variable''' enthalten. Werden zwei '''Terme''' mit einem Gleichheitszeichen verbunden, entsteht eine '''Gleichung'''. Es gibt verschiedene Arten von Gleichungen. Wichtige Arten sind die '''linearen''' und die '''quadratischen''' Gleichungen. | ||
</div>| 3= Lösung|Farbe={{Farbe|grün|dunkel}}}} | </div>| 3= Lösung|Farbe={{Farbe|grün|dunkel}}}} | ||
{{Box|Begriffstraining | | {{Box|Begriffstraining | | ||
Teste dein Wissen! {{LearningApp|width:100%|height:700px|app=pgvznoxrk23}} | Teste dein Wissen! {{LearningApp|width:100%|height:700px|app=pgvznoxrk23}} | ||
|Üben|Farbe={{Farbe|orange|heller}}}} | |Üben|Farbe={{Farbe|orange|heller}}}} | ||
=='''2.Terme '''== | =='''2.Terme '''== | ||
=== '''Terme aufstellen''' === | === '''Terme aufstellen''' === | ||
{{Box|Terme in Sachsituationen|Du hast gelernt, Sachsituationen mit Hilfe von Termen zu beschreiben. Hier kannst du dein Wissen testen. | {{Box|Terme in Sachsituationen|Du hast gelernt, Sachsituationen mit Hilfe von Termen zu beschreiben. Hier kannst du dein Wissen testen. | ||
a) | a) | ||
{{H5p-zum|id= 12396|height=250}} | {{H5p-zum|id= 12396|height=250}} | ||
b) | b) | ||
{{H5p-zum|id= 21668|height=250}} | {{H5p-zum|id= 21668|height=250}} | ||
|Arbeitsmethode|Farbe={{Farbe|orange}}}} | |Arbeitsmethode|Farbe={{Farbe|orange}}}} | ||
| Zeile 50: | Zeile 35: | ||
{{LearningApp|app=pynxyt0qk20|width=100%|height=350px}} | {{LearningApp|app=pynxyt0qk20|width=100%|height=350px}} | ||
|Arbeitsmethode|Farbe={{Farbe|orange}}}} | |Arbeitsmethode|Farbe={{Farbe|orange}}}} | ||
{{Box|Info|Überflüssige Malpunkte werden nicht notiert. |Kurzinfo||Farbe={{Farbe|sekundär-1|x-heller}}}} | {{Box|Info|Überflüssige Malpunkte werden nicht notiert. |Kurzinfo||Farbe={{Farbe|sekundär-1|x-heller}}}} | ||
| Zeile 100: | Zeile 84: | ||
<math> = 5 \cdot 4 {x} {x} {y} </math> <math> = 20 {x^2}{y} </math> <br/> | <math> = 5 \cdot 4 {x} {x} {y} </math> <math> = 20 {x^2}{y} </math> <br/> | ||
g) <math> 2{x}(-7{x^2y})(-3{y^3}) </math> <math> = 2 \cdot (-7) \cdot (-3) {x} {x^2} {y} {y^3} </math> <math> = 42{x^3}{y^4} </math> <br/> | g) <math> 2{x}(-7{x^2y})(-3{y^3}) </math> <math> = 2 \cdot (-7) \cdot (-3) {x} {x^2} {y} {y^3} </math> <math> = 42{x^3}{y^4} </math> <br/> | ||
|3=Üben}} | |3=Üben}} | ||
| Zeile 113: | Zeile 96: | ||
{{Box|Termtraining. |Füge die zugehörigen Terme zusammen. Du kannst hierfür deinen Stift und Papier nutzen.{{LearningApp|width:75%|height:250px|app=2954651}} | {{Box|Termtraining. |Füge die zugehörigen Terme zusammen. Du kannst hierfür deinen Stift und Papier nutzen.{{LearningApp|width:75%|height:250px|app=2954651}} | ||
|Üben|Farbe={{Farbe|orange|heller}}}} | |Üben|Farbe={{Farbe|orange|heller}}}} | ||
=== Klammern in Termen === | === Klammern in Termen === | ||
{{Box|Info| |Kurzinfo|Zunächst geht es um das sogenannte '''Ausmultiplizieren''', das heißt das '''Auflösen von Klammern'''. |Farbe={{Farbe|sekundär-1|x-heller}}}} | |||
{{Box|1 = Auflösen von Klammern| | {{Box|1 = Auflösen von Klammern| | ||
2 = Erkläre mit Hilfe der Abbildung, dass für das Auflösen von Klammern gilt: | 2 = Erkläre mit Hilfe der Abbildung, dass für das Auflösen von Klammern gilt: | ||
[[Datei:Distr1.png|mini]] | [[Datei:Distr1.png|mini]] | ||
<math>{\color{green}a}(b+c) = {\color{green}a}b + {\color{green}a}c</math>. | <math>{\color{green}a}(b+c) = {\color{green}a}b + {\color{green}a}c</math>.<br/> | ||
<math>(b+c){\color{green}a} = b{\color{green}a} + {\color{green}a} </math>.<br/> | |||
<math>(b+c){\color{green}a} = b{\color{green}a} + {\color{green}a} </math>. | |||
Formuliere die Regel in eigenen Worten. Wende sie auf das Beispiel a = 2, b = 5 und c = 3 an. Kontrolliere dann deine Lösung. | Formuliere die Regel in eigenen Worten. Wende sie auf das Beispiel a = 2, b = 5 und c = 3 an. Kontrolliere dann deine Lösung. | ||
{{Lösung versteckt|1= Man multipliziert einen <span style="color: green">'''Faktor'''</span> mit einer Klammer, indem man den Faktor mit jedem einzelnen Glied in der Klammer multipliziert. | {{Lösung versteckt|1= Man multipliziert einen <span style="color: green">'''Faktor'''</span> mit einer Klammer, indem man den Faktor mit jedem einzelnen Glied in der Klammer multipliziert. | ||
[[Datei:Ausmultiplizieren 1.png|mini | links | thumb ]] | [[Datei:Ausmultiplizieren 1.png|mini | links | thumb ]] | ||
| Zeile 135: | Zeile 113: | ||
<math>(5+3) \cdot {\color{green}2} = 5 \cdot {\color{green}2} + 3\cdot {\color{green}2} = 10 + 6 = 16</math>. | <math>(5+3) \cdot {\color{green}2} = 5 \cdot {\color{green}2} + 3\cdot {\color{green}2} = 10 + 6 = 16</math>. | ||
|2= Lösung|3=einklappen}}<br /> | |2= Lösung|3=einklappen}}<br /> | ||
Erinnerung | Erinnerung | ||
# Achte darauf, ob in der Klammer eine Summe oder Differenz steht, denn: <math>a(b{\color{red}-}c) = a \cdot b {\color{red}-} a\cdot c </math> | # Achte darauf, ob in der Klammer eine Summe oder Differenz steht, denn: <math>a(b{\color{red}-}c) = a \cdot b {\color{red}-} a\cdot c </math> | ||
# Bei Minusklammern, also wenn vor der Klammer ein '''negativer Faktor''' steht, drehen sich die Vorzeichen von jedem Glied in der Klammer um: | # Bei Minusklammern, also wenn vor der Klammer ein '''negativer Faktor''' steht, drehen sich die Vorzeichen von jedem Glied in der Klammer um: | ||
<math> {\color{red}-}a(b{\color{red}+}c) = {\color{red}-}ab {\color{red}-} ac</math>. | <math> {\color{red}-}a(b{\color{red}+}c) = {\color{red}-}ab {\color{red}-} ac</math>. | ||
<math>{\color{red}-}a({\color{red}-}b{\color{red}+}c) = ab {\color{red}-} ac</math>. | <math>{\color{red}-}a({\color{red}-}b{\color{red}+}c) = ab {\color{red}-} ac</math>. | ||
b) | b) | ||
Erkläre mit Hilfe der Abbildung, dass für die Multiplikation zweier Summen oder Differenzen folgende Regel gilt: | Erkläre mit Hilfe der Abbildung, dass für die Multiplikation zweier Summen oder Differenzen folgende Regel gilt: | ||
<math> (a+b) (c+d) = ac + ad + bc + bd </math>. Erkläre die Regel in eigenen Worten und wende sie auf das Beispiel a = 2, b = 3, c = 7 und d = -2 an. Kontrolliere dann deine Lösung | <math> (a+b) (c+d) = ac + ad + bc + bd </math>. Erkläre die Regel in eigenen Worten und wende sie auf das Beispiel a = 2, b = 3, c = 7 und d = -2 an. Kontrolliere dann deine Lösung | ||
[[Datei:Distr2.png|mini]] | [[Datei:Distr2.png|mini]] | ||
{{Lösung versteckt|1= Zwei Summen (oder Differenzen) werden miteinander multipliziert, indem man '''jeden Summanden der ersten Klammer mit jedem Summanden der zweiten Klammer multipliziert:''' | {{Lösung versteckt|1= Zwei Summen (oder Differenzen) werden miteinander multipliziert, indem man '''jeden Summanden der ersten Klammer mit jedem Summanden der zweiten Klammer multipliziert:''' | ||
[[Datei:Ausmultiplizieren 2.png|400px | links| thumb]] <br /> <br /> | [[Datei:Ausmultiplizieren 2.png|400px | links| thumb]] <br /> <br /> | ||
Es ist | Es ist | ||
| Zeile 162: | Zeile 131: | ||
(2+3)(7-2) = 2 \cdot 7 - 2 \cdot 2 + 3 \cdot 7 - 3 \cdot 2 = 14 - 4 + 21 - 6 = 25 | (2+3)(7-2) = 2 \cdot 7 - 2 \cdot 2 + 3 \cdot 7 - 3 \cdot 2 = 14 - 4 + 21 - 6 = 25 | ||
<br /> <br /> <br /> <br /> | <br /> <br /> <br /> <br /> | ||
|2= Lösung|3=einklappen}}<br /> | |2= Lösung|3=einklappen}}<br /> | ||
| Zeile 168: | Zeile 136: | ||
<math>{\color{green}2}(3x - 1) = {\color{green}2} \cdot 3x - {\color{green}2} \cdot 1 = 6x - 2</math>. | <math>{\color{green}2}(3x - 1) = {\color{green}2} \cdot 3x - {\color{green}2} \cdot 1 = 6x - 2</math>. | ||
<math>{\color{red}-}(a{\color{red}+}b) = {\color{red}-}a {\color{red}-} b</math>. | <math>{\color{red}-}(a{\color{red}+}b) = {\color{red}-}a {\color{red}-} b</math>. | ||
<math>{\color{red}-}(a{\color{red}-}b) = {\color{red}-}a {\color{red}+} b</math>. | <math>{\color{red}-}(a{\color{red}-}b) = {\color{red}-}a {\color{red}+} b</math>. | ||
|2=Bei Bedarf findest du hier weitere Beispiele zum Thema Ausmultiplizieren |3=Verbergen}} | |2=Bei Bedarf findest du hier weitere Beispiele zum Thema Ausmultiplizieren |3=Verbergen}} | ||
|3= Arbeitsmethode|Farbe={{Farbe|orange}}}} | |3= Arbeitsmethode|Farbe={{Farbe|orange}}}} | ||
{{Box|1 = Merke: Auflösen von Klammern|2 = Ergänze den Lückentext. Prüfe das Ergebnis und übertrage die Lösung in den Kasten "Klammern in Termen" in deinem Begleitheft. | {{Box|1 = Merke: Auflösen von Klammern|2 = Ergänze den Lückentext. Prüfe das Ergebnis und übertrage die Lösung in den Kasten "Klammern in Termen" in deinem Begleitheft. | ||
| Zeile 191: | Zeile 156: | ||
{{Box|1 = Training zum Ausmultiplizieren |2 =In dieser Aufgabe kannst du das ''Ausmultiplizieren'' üben. Ordne jedem Klammerterm die richtige ausmultiplizierte Lösung zu. Nimm dir einen Zettel für Nebenrechnungen zur Hilfe. | {{Box|1 = Training zum Ausmultiplizieren |2 =In dieser Aufgabe kannst du das ''Ausmultiplizieren'' üben. Ordne jedem Klammerterm die richtige ausmultiplizierte Lösung zu. Nimm dir einen Zettel für Nebenrechnungen zur Hilfe. | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
a) <math> (5b+c+3d)\cdot a = </math> '''<math> 5ab+ac+3ad </math>''' <br /> | a) <math> (5b+c+3d)\cdot a = </math> '''<math> 5ab+ac+3ad </math>''' <br /> | ||
b) <math> (5a+4b)\cdot 4 = </math> '''<math> 16b+20a </math>''' <br /> | b) <math> (5a+4b)\cdot 4 = </math> '''<math> 16b+20a </math>''' <br /> | ||
| Zeile 201: | Zeile 165: | ||
|3 = Üben|Farbe={{Farbe|orange|heller}}}} | |3 = Üben|Farbe={{Farbe|orange|heller}}}} | ||
'''Ausklammern''' | {{Box|Info| |Kurzinfo|Jetzt geht es um den umgekehrten Weg. Beim '''Ausklammern''' wird eine Summe in ein Produkt umgewandelt, es werden also '''Klammern hinzugefügt'''. | ||
Dies ist nur dann möglich, wenn die Summanden '''gemeinsame Faktoren''' haben.|Farbe={{Farbe|sekundär-1|x-heller}}}} | |||
Dies ist nur dann möglich, wenn die Summanden gemeinsame Faktoren haben. | |||
{{Box|1=Ausklammern|2 = Suche in den LearningApps nach gemeinsamen Faktoren der Summenden und klammere diese dann aus. | {{Box|1=Ausklammern|2 = Suche in den LearningApps nach gemeinsamen Faktoren der Summenden und klammere diese dann aus. | ||
| Zeile 212: | Zeile 175: | ||
= <span style="color:red">4x</span>⋅2 + <span style="color:red">4x</span>⋅3y<br> | = <span style="color:red">4x</span>⋅2 + <span style="color:red">4x</span>⋅3y<br> | ||
= <span style="color:red">4x</span>⋅(2 + 3y) | = <span style="color:red">4x</span>⋅(2 + 3y) | ||
|2=Beispiel |3=Beispiel ausblenden}} | |2=Beispiel |3=Beispiel ausblenden}} | ||
{{LearningApp|app=p5pcm6z0a20|width=100%|height=400px}} | {{LearningApp|app=p5pcm6z0a20|width=100%|height=400px}} | ||
{{LearningApp|app=p1on72s7319|width=100%|height=400px}} | {{LearningApp|app=p1on72s7319|width=100%|height=400px}} | ||
|3=Arbeitsmethode|Farbe={{Farbe|orange}}}} | |3=Arbeitsmethode|Farbe={{Farbe|orange}}}} | ||
== '''3. Gleichungen''' == | == '''3. Gleichungen''' == | ||
{{Box|Idee|Lineare und quadratische Gleichungen. Eine '''lineare Gleichung''' ist eine Gleichung 1. Grades. Das heißt: Die Variable x hat als Exponenten höchstens die Zahl 1: | {{Box|Idee|Lineare und quadratische Gleichungen. Eine '''lineare Gleichung''' ist eine Gleichung 1. Grades. Das heißt: Die Variable x hat als Exponenten höchstens die Zahl 1: | ||
| Zeile 232: | Zeile 189: | ||
Eine '''quadratische Gleichung''' ist eine Gleichung 2. Grades. Das heißt: Die Variable x hat als Exponenten höchstens die Zahl 2. Zum Beispiel: <math> x^2 = 9 </math> oder <math> 2x^2 +5x - 8 = 0 </math>. Die Verfahren zur Lösung solcher Gleichungen sollst du jetzt wiederholen. | Eine '''quadratische Gleichung''' ist eine Gleichung 2. Grades. Das heißt: Die Variable x hat als Exponenten höchstens die Zahl 2. Zum Beispiel: <math> x^2 = 9 </math> oder <math> 2x^2 +5x - 8 = 0 </math>. Die Verfahren zur Lösung solcher Gleichungen sollst du jetzt wiederholen. | ||
|Unterrichtsidee }} | |Unterrichtsidee }} | ||
{{Box|1 = Verfahren zum Lösen linearer Gleichungen| 2 = Das Verfahren zum Lösen linearer Gleichungen hast du bereits kennengelernt. Die folgende Learning-App hilft dir, dich zu erinnern. | {{Box|1 = Verfahren zum Lösen linearer Gleichungen| 2 = Das Verfahren zum Lösen linearer Gleichungen hast du bereits kennengelernt. Die folgende Learning-App hilft dir, dich zu erinnern. | ||
{{LearningApp|app=p3j3a7sia23|width=100%|height=400px}} | {{LearningApp|app=p3j3a7sia23|width=100%|height=400px}} | ||
|3 = Arbeitsmethode|Farbe={{Farbe|orange}}}} | |3 = Arbeitsmethode|Farbe={{Farbe|orange}}}} | ||
| Zeile 247: | Zeile 201: | ||
# '''Bringe die Summanden mit Variablen und die Summanden ohne Variablen jeweils auf eine Seite, fasse sie zusammen bzw. ordne sie.''' | # '''Bringe die Summanden mit Variablen und die Summanden ohne Variablen jeweils auf eine Seite, fasse sie zusammen bzw. ordne sie.''' | ||
# '''Dividiere durch den Faktor vor der Variable.''' | # '''Dividiere durch den Faktor vor der Variable.''' | ||
</div> | </div> | ||
Beispiel: <br> | Beispiel: <br> | ||
[[Datei:Beispiel Gleichung Merkkasten.jpg]] | [[Datei:Beispiel Gleichung Merkkasten.jpg]] | ||
|3 = Merksatz}} | |3 = Merksatz}} | ||
{{Box|1 = Training: lineare Gleichungen lösen |2= Löse die Gleichungen. Führe, wenn möglich, eine Probe durch. Denke daran: Eine Probe kann nur durchgeführt werden, wenn es mindestens eine Lösung für die Gleichung gibt. | {{Box|1 = Training: lineare Gleichungen lösen |2= Löse die Gleichungen. Führe, wenn möglich, eine Probe durch. Denke daran: Eine Probe kann nur durchgeführt werden, wenn es mindestens eine Lösung für die Gleichung gibt. | ||
'''a)''' <math>2a-64=5+a</math> | '''a)''' <math>2a-64=5+a</math> | ||
{{Lösung versteckt|1=<math>\begin{align} & & a-64 &=5+a & &\mid +64\\ | {{Lösung versteckt|1=<math>\begin{align} & & a-64 &=5+a & &\mid +64\\ | ||
\Leftrightarrow & & a &=69 \\ | \Leftrightarrow & & a &=69 \\ | ||
\end{align}</math> | \end{align}</math> | ||
Probe: | Probe: | ||
<math>\begin{align} & & 69-64 &=5 \\ | <math>\begin{align} & & 69-64 &=5 \\ | ||
\Leftrightarrow & & 69-64 &=5\\ | \Leftrightarrow & & 69-64 &=5\\ | ||
\Leftrightarrow & & 5 &=5 | \Leftrightarrow & & 5 &=5 | ||
\end{align}</math> | \end{align}</math> | ||
|2=Lösung|3=Lösung ausblenden}} | |2=Lösung|3=Lösung ausblenden}} | ||
| Zeile 280: | Zeile 224: | ||
\Leftrightarrow & & x &=3\\ | \Leftrightarrow & & x &=3\\ | ||
\end{align}</math> | \end{align}</math> | ||
Probe: | Probe: | ||
<math>\begin{align} & & 3\cdot 3+7&=16\\ | <math>\begin{align} & & 3\cdot 3+7&=16\\ | ||
| Zeile 294: | Zeile 237: | ||
\Leftrightarrow & & -1 &=1 | \Leftrightarrow & & -1 &=1 | ||
\end{align}</math> | \end{align}</math> | ||
Das ist ein Widerspruch. Deshalb ist die Lösungsmenge leer: <math>\mathbb{L}=\{\}</math>. Hier ist keine Probe durch Einsetzen möglich, weil die Lösungsmenge leer ist. | Das ist ein Widerspruch. Deshalb ist die Lösungsmenge leer: <math>\mathbb{L}=\{\}</math>. Hier ist keine Probe durch Einsetzen möglich, weil die Lösungsmenge leer ist. | ||
|2=Lösung|3=Lösung ausblenden}} | |2=Lösung|3=Lösung ausblenden}} | ||
| Zeile 308: | Zeile 250: | ||
& & \mathbb{L}=\{1\} | & & \mathbb{L}=\{1\} | ||
\end{align}</math> | \end{align}</math> | ||
Probe: | Probe: | ||
<math>\begin{align} & & \frac{1}{2 \cdot 1} &=0,5 & &\\ | <math>\begin{align} & & \frac{1}{2 \cdot 1} &=0,5 & &\\ | ||
\Leftrightarrow & & \frac{1}{2} &=0,5 & &\\ | \Leftrightarrow & & \frac{1}{2} &=0,5 & &\\ | ||
| Zeile 326: | Zeile 266: | ||
& & \mathbb{L}=\{0,5\} | & & \mathbb{L}=\{0,5\} | ||
\end{align}</math> | \end{align}</math> | ||
Probe: | Probe: | ||
<math>\begin{align} & & 0\cdot (0-5)&=0\\ | <math>\begin{align} & & 0\cdot (0-5)&=0\\ | ||
\Leftrightarrow & & 0&=0 | \Leftrightarrow & & 0&=0 | ||
\end{align}</math> | \end{align}</math> | ||
<math>\begin{align} & & 5\cdot (5-5)&=0\\ | <math>\begin{align} & & 5\cdot (5-5)&=0\\ | ||
\Leftrightarrow & & 5\cdot 0&=0\\ | \Leftrightarrow & & 5\cdot 0&=0\\ | ||
| Zeile 340: | Zeile 277: | ||
Sprinteraufgabe: | Sprinteraufgabe: | ||
'''f)''' <math>\frac{3}{z+1}=-\frac{5}{2z-1}</math> | '''f)''' <math>\frac{3}{z+1}=-\frac{5}{2z-1}</math> | ||
{{Lösung versteckt|1=Versuche die Variablen mit Hilfe der Multiplikation aus dem Nenner zu bekommen.|2=Tipp|3=Tipp ausblenden}} | {{Lösung versteckt|1=Versuche die Variablen mit Hilfe der Multiplikation aus dem Nenner zu bekommen.|2=Tipp|3=Tipp ausblenden}} | ||
| Zeile 354: | Zeile 290: | ||
& & \mathbb{L}=\{-\frac{2}{11}\} | & & \mathbb{L}=\{-\frac{2}{11}\} | ||
\end{align}</math> | \end{align}</math> | ||
Probe: | Probe: | ||
<math>\begin{align} & & \frac{3}{- \frac{2}{11} +1} &= - \frac{5}{2 \cdot (- \frac{2}{11}) -1} & &\\ | <math>\begin{align} & & \frac{3}{- \frac{2}{11} +1} &= - \frac{5}{2 \cdot (- \frac{2}{11}) -1} & &\\ | ||
\Leftrightarrow & & \frac{3}{\frac{9}{11}} &= - \frac{5}{- \frac{4}{11} -1} & &\\ | \Leftrightarrow & & \frac{3}{\frac{9}{11}} &= - \frac{5}{- \frac{4}{11} -1} & &\\ | ||
| Zeile 365: | Zeile 299: | ||
\end{align}</math> | \end{align}</math> | ||
|2=Lösung|3=Lösung ausblenden}} | |2=Lösung|3=Lösung ausblenden}} | ||
|3 = Üben|Farbe={{Farbe|orange|heller}}}} | |3 = Üben|Farbe={{Farbe|orange|heller}}}} | ||
| Zeile 422: | Zeile 353: | ||
</math>}} | </math>}} | ||
|3 = Arbeitsmethode|Farbe={{Farbe|orange}}}} | |3 = Arbeitsmethode|Farbe={{Farbe|orange}}}} | ||
| Zeile 468: | Zeile 396: | ||
\end{alignat} | \end{alignat} | ||
</math>|2=Lösung anzeigen|3=Lösung ausblenden}} | </math>|2=Lösung anzeigen|3=Lösung ausblenden}} | ||
|3 = Arbeitsmethode|Farbe={{Farbe|orange}}}} | |3 = Arbeitsmethode|Farbe={{Farbe|orange}}}} | ||
=='''Vernetzte Aufgaben '''== | =='''Vernetzte Aufgaben '''== | ||
{{Box|Info| |Kurzinfo|Die folgenden Aufgaben sind thematisch geordnet. Du darfst über die Reihenfolge der Bearbeitung frei entscheiden.|Farbe={{Farbe|sekundär-1|x-heller}}}} | |||
{{Box| | |||
===Zahlenrätsel=== | ===Zahlenrätsel=== | ||
| Zeile 556: | Zeile 473: | ||
Leon ist heute <math>12</math> Jahre alt und seine Mutter ist heute <math>36</math> Jahre alt.|2=Lösung | Leon ist heute <math>12</math> Jahre alt und seine Mutter ist heute <math>36</math> Jahre alt.|2=Lösung | ||
|3=Lösung ausblenden}}| Arbeitsmethode}} | |3=Lösung ausblenden}}| Arbeitsmethode}} | ||
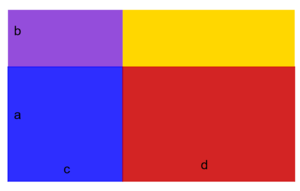
{{Box|1 = Flächeninhalt |2= Klicke alle Terme an, die den Flächeninhalt der Fläche beschreiben. | |||
{{LearningApp|app=pxj3hfqot18|width=100%|height=400px}} | |||
{{Lösung versteckt|1=Worin liegt der Unterschied zwischen Flächeninhalt und Umfang?|2= Tipp 1|3=schließen}} | |||
{{Lösung versteckt|1=Mache dir bewusst, welche Bedeutung die einzelnen Glieder der Terme haben.|2=Tipp 2|3=schließen}} | |||
{{Lösung versteckt|1=Zeichne die Rechtecke, die durch die einzelnen Term-Glieder repräsentiert werden, in dein Heft und überprüfe, ob sich daraus die Figur zusammen setzen lässt.|2=Tipp 3|3=schließen}} | |||
|3 = Üben|Farbe={{Farbe|orange|heller}}}} | |||
===Rechnen mit Gleichungen im Sachzusammenhang=== | ===Rechnen mit Gleichungen im Sachzusammenhang=== | ||
Version vom 22. März 2023, 07:00 Uhr
In diesem Lernpfad geht es um das Vertiefen deines Wissens über Terme, Variablen und Gleichungen.
Du findest hier eine Wiederholung zu den Begriffen und Übungsaufgaben zu den Themen Terme aufstellen, Terme umformen und Gleichungen lösen. .
1.Terme, Variablen und Gleichungen
2.Terme
Terme aufstellen
Terme vereinfachen
a) =
b) =
c) =
d) =
e) =
f)
Klammern in Termen
3. Gleichungen
Vernetzte Aufgaben
Zahlenrätsel
Rechnen mit Gleichungen im Sachzusammenhang
Was ist gegeben?
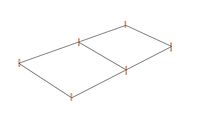
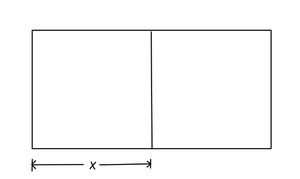
zwei flächengleiche Flächen (Quadrat und Rechteck)
x = Seitenlänge der quadratischen Weide
x - 4 = eine Seitenlänge der rechteckigen Weide (3m kürzer)
x + 6 = andere Seitenlänge der rechteckigen Weide (5m länger)
Die beiden Weiden sind flächengleich, d.h. ihr Flächeninhalt ist gleich.
Benutze zum Aufstellen der Gleichung die Formeln für die Berechnung des Flächeninhaltes eines Quadrats und eines Rechtecks.
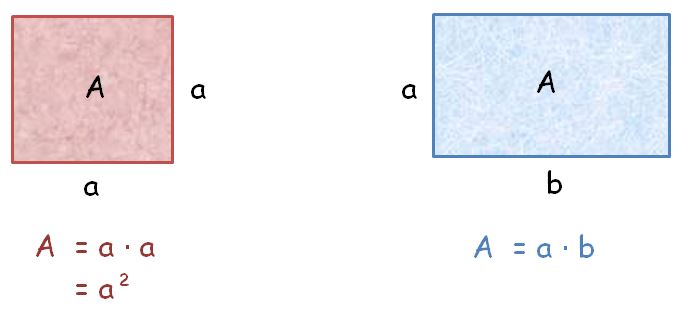
Beide Flächen sind gleich groß, daher lautet die Gleichung:
x² = (x – 4) (x + 6)
Versuche nun x zu berechnen. Löse hierfür zunächst die Klammern auf.Du hast nun herausgefunden, dass die Länge und Breite der quadratischen Weide je 12m beträgt. Damit kannst du jetzt die Seitenlängen der rechteckigen Weide berechnen. Setze hierfür x = 12 in deine aufgestellten Terme ein:
- x - 4 (eine Seitenlänge des Rechtecks)
- x + 6 (andere Seitenlänge des Rechtecks)