Jule Volbers/Testseite: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 485: | Zeile 485: | ||
{{Lösung versteckt|1=Zeichne die Rechtecke, die durch die einzelnen Term-Glieder repräsentiert werden, in dein Heft und überprüfe, ob sich daraus die Figur zusammen setzen lässt.|2=Tipp 3|3=schließen}} | {{Lösung versteckt|1=Zeichne die Rechtecke, die durch die einzelnen Term-Glieder repräsentiert werden, in dein Heft und überprüfe, ob sich daraus die Figur zusammen setzen lässt.|2=Tipp 3|3=schließen}} | ||
|3 = Üben|Farbe={{Farbe|orange|heller}}}} | |3 = Üben|Farbe={{Farbe|orange|heller}}}} | ||
===Zahlenrätsel=== | |||
{{Box | Aufgabe 3: Finde die gesuchte Zahl | | |||
Wenn man zur Zahl <math>12</math> das Doppelte einer Zahl addiert, so erhält man das Vierfache der gesuchten Zahl. Stelle eine geeignete Gleichung auf und gib die gesuchte Zahl an. | |||
{{Lösung versteckt|1=Überlege dir, wie man das Doppelte und das Vierfache einer Zahl als Term schreibt.|2=Tipp|3=Tipp ausblenden}} | |||
{{Lösung versteckt|1=Zunächst übersetzen wir die Informationen aus der Aufgabenstellung in eine mathematische Schreibweise: | |||
Das Doppelte einer Zahl: <math>2x</math> | |||
Zur Zahl <math>12</math> das Doppelte einer Zahl addieren: <math>2x+12</math>. Dies wird die '''linke Seite''' der Gleichung bilden. | |||
Das Vierfache der gesuchten Zahl: <math>4x</math>. Dies ist die '''rechte Seite''' der Gleichung. | |||
Wir erhalten also die Gleichung: | |||
<math>2x+12=4x</math>. | |||
Um das gesuchte <math>x</math> zu finden, lösen wir die Gleichung, indem wir sie nach <math>x</math> umstellen. Achte darauf alle Umformungen immer auf beiden Seiten der Gleichung durchzuführen. | |||
<math>\begin{align}& & 2x+12 & = 4x & &\mid -2x\\ \Leftrightarrow & & 12 & = 2x & &\mid :2\\ \Leftrightarrow & & 6 & = x \end{align} | |||
</math> | |||
Die gesuchte Zahl ist <math>6</math>. | |||
Probe: | |||
<math>\begin{align} & & 2\cdot 6+12&=4\cdot 6 \\ | |||
\Leftrightarrow & &24&=24 \end{align}</math>|2=Lösung | |||
|3=Lösung ausblenden}}| Arbeitsmethode}} | |||
{{Box | Aufgabe 4: Alter der Mutter|Die Mutter von Leon ist <math>3</math>-mal so alt wie er. In <math>12</math> Jahren wird sie doppelt so alt sein wie Leon. Wie alt sind Leon und seine Mutter heute? | |||
{{Lösung versteckt|1=Beachte, dass sich das doppelte Alter auf das Alter in <math>12</math> Jahren bezieht.|2=Tipp|3=Tipp ausblenden}} | |||
{{Lösung versteckt|1=Bezeichne mit <math>M</math> das Alter der Mutter und mit <math>L</math> das Alter von Leon. | |||
Die erste Gleichung ist <math>\begin{align}M=3L\end{align}</math>,da die Mutter von Leon 3-mal so alt ist wie er. | |||
Außerdem gilt die zweite Gleichung <math>\begin{align}M+12=2(L+12)\end{align}</math>. Die linke Seite der Gleichung beschreibt das Alter der Mutter in 12 Jahren. Dies entspricht der rechten Seite der Gleichung, da das Alter der Mutter in 12 Jahren dann das doppelte des Alters von Leon in 12 Jahren beträgt. | |||
Setze nun <math>\begin{align}M=3L \end{align}</math> in die zweite Gleichung ein: | |||
<math>\begin{align}\\ | |||
\Leftrightarrow & & 3L+12&=2L+24 & &\mid -12\\ | |||
\Leftrightarrow & & 3L&=2L+12 & &\mid -2L\\ | |||
\Leftrightarrow & & L=12 | |||
\end{align}</math> | |||
Leon ist heute also 12 Jahre alt. | |||
Um das Alter der Mutter zu bestimmen, setzten wir <math>L=12</math> in die erste Gleichung ein: | |||
<math>\begin{align} & & M=3 \cdot 12 = 36 \end{align}</math> | |||
Die Mutter ist heute also 36 Jahre alt. | |||
Probe erste Gleichung: | |||
<math>\begin{align}\\ & & 3\cdot 12=36 & &\\ | |||
\Leftrightarrow & & 36=36 & | |||
\end{align}</math> | |||
Probe zweite Gleichung: | |||
<math>\begin{align}\\ & & 36+12=2\cdot(12+12) & &\\ | |||
\Leftrightarrow & & 48=48 & | |||
\end{align}</math> | |||
Leon ist heute <math>12</math> Jahre alt und seine Mutter ist heute <math>36</math> Jahre alt.|2=Lösung | |||
|3=Lösung ausblenden}}| Arbeitsmethode}} | |||
===Rechnen mit Gleichungen im Sachzusammenhang=== | |||
{{Box | Aufgabe 5: Zwei-Felder-Ball-Feld abstecken | | |||
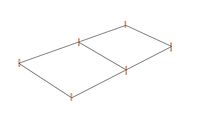
[[Datei:269A89E6-8A5A-4969-B953-21A412026976.jpg|200px|Zwei-Felder-Ball-Feld|rechts]]Nick und Tom sollen für ein Sportfest ein Zwei-Felder-Ball-Feld abstecken. Dafür sollen sie ein <math>66</math> m langes Seil und sechs Pfosten verwenden. Für das Umwickeln aller Pfosten werden insgesamt drei Meter Seil benötigt. Das Spielfeld soll aus zwei gleichgroßen quadratischen Flächen bestehen. Wie lang ist eine Seite von einer der quadratischen Flächen, wenn man davon ausgeht, dass Nick und Tom das gesamte Seil benutzen? | |||
{{Lösung versteckt|1=Um die Gleichung aufzustellen, benötigst du den Umfang des Spielfeldes.|2=Tipp 1|3=Tipp 1 ausblenden}} | |||
{{Lösung versteckt|1=Benutze die Skizze, um einen Term für den Umfang des Spielfeldes aufzustellen. [[Datei:Skizze neu.jpg|mini|Skizzierung des Spielfeldes]] Beachte, dass zusätzlich Seil für das Abspannen an den Pfosten benötigt wird.|2=Tipp 2|3=Tipp 2 ausblenden}} | |||
{{Lösung versteckt|1=Die gesuchte Seitenlänge bezeichnen wir mit <math>x</math>. [[Datei:Skizze neu.jpg|mini|Skizzierung des Spielfeldes]] Den Umfang des Spielfeldes erhalten wir durch den Term <math>7x</math>. | |||
Wir erhalten die Gleichung: <math>7x+3=66</math>, da insgesamt <math>66</math> Meter Seil zur Verfügung stehen und drei Meter Seil für die Abspannung an den Pfosten benötigt werden. | |||
Diese Gleichung können wir lösen: | |||
<math>\begin{align} & & 7x+3 &=66 & &\mid -3\\ | |||
\Leftrightarrow & & 7x &=63 & &\mid :7\\ | |||
\Leftrightarrow & & x &=9 | |||
\end{align} </math> | |||
Probe: | |||
<math>\begin{align} & & 7 \cdot 9 +3 &=66\\ | |||
\Leftrightarrow & & 63 + 3 &=66\\ | |||
\Leftrightarrow & & 66 &=66\\ | |||
\end{align}</math> | |||
Eine Seite ist <math>9</math> m lang.|2=Lösung|3=Lösung ausblenden}} | |||
| Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | |||
{{Box | Aufgabe 6: Getränkelager füllen | | |||
In einem Lager eines Restaurants sollen möglichst viele <math>35</math> cm hohe Getränkekisten übereinander gestapelt werden. Die Raumhöhe beträgt <math>2,20</math> m. | |||
'''a)''' Wie viele Getränkekisten können übereinander gestapelt werden? Stelle eine Gleichung auf und berechne. | |||
'''b)''' Eine Getränkekiste ist <math>40</math> cm lang und <math>40</math> cm breit. Das Lager hat eine Lagerfläche von <math>10</math> m <math>\cdot</math> <math>10</math> m. Wie viele Getränkekisten finden insgesamt im Lager Platz? | |||
{{Lösung versteckt|1=Beachte die Umrechnung der Einheiten.|2=allgemeiner Tipp|3=Tipp 1 ausblenden}} | |||
{{Lösung versteckt|1=Berechne zuerst, wie viele Getränkekisten auf dem Boden der Lagerfläche Platz finden.|2=Tipp zu b)|3=Tipp 2 ausblenden}} | |||
{{Lösung versteckt|1= '''a)''' Zuerst wird die Höhe einer Getränkekiste in Meter umgerechnet: | |||
<math>35 </math> cm <math>=0,35</math> m. | |||
Jetzt kann die Gleichung aufgestellt werden: | |||
<math>0,35\cdot x=2,20</math>, | |||
wobei <math>0,35</math> die Höhe einer Getränkekiste in Metern und <math>2,20</math> die Höhe des Lagerraumes in Metern angibt. Die Variable <math>x</math> bezeichnet in der Gleichung die Anzahl der Kisten, die in den Lagerraum gestellt werden können. | |||
Jetzt wird <math>x</math> mit Hilfe der aufgestellten Gleichung berechnet: | |||
<math>\begin{align} & & 0,35\cdot x &=2,20 & &\mid :0,35\\ | |||
\Leftrightarrow & & x &\approx 6,29 & &\\ | |||
\end{align} </math> | |||
Probe: | |||
<math>\begin{align} & & 0,35\cdot 6,29 \approx 2,20 & &\\ | |||
\Leftrightarrow & & 2,20 \approx 2,20 & &\\ | |||
\end{align} </math> | |||
Das Ergebnis <math>6,29</math> wird auf <math>6</math> abgerundet, da nur ganze Kisten gestapelt werden können. Es können in dem Lagerraum also <math>6</math> Getränkekisten übereinander gestapelt werden.|2=Lösung zu a)|3=Lösung ausblenden}} | |||
{{Lösung versteckt|1='''b)''' Zuerst legen wir den Boden der Lagerfläche mit Getränkekisten aus. Dazu stellen wir folgende Gleichung auf: | |||
<math>\begin{align} & & 10\cdot 10 &=0,4\cdot 0,4\cdot x & &\\ | |||
\Leftrightarrow & & 100 &=0,16\cdot x & &\mid :0,16\\ | |||
\Leftrightarrow & & 625 &=x | |||
\end{align} </math> | |||
Probe: | |||
<math>\begin{align} & & 10\cdot 10&=0,4\cdot 0,4\cdot 625 & &\\ | |||
\Leftrightarrow & & 100 &=0,16\cdot 625 & &\\ | |||
\Leftrightarrow & & 100 &=100 | |||
\end{align} </math> | |||
In dieser Gleichung gibt der Teil <math>10\cdot 10</math> die Grundfläche der Lagerfläche in m² an. Der Teil <math>0,4\cdot 0,4</math> berechnet die Grundfläche der Getränkekisten in m². Die Variable <math>x</math> bezeichnet die Anzahl der Getränkekisten. | |||
Wir wissen nun also, dass <math>625</math> Getränkekisten auf dem Boden der Lagerfläche Platz finden. | |||
Aus Aufgabenteil '''a)''' wissen wir bereits, dass <math>6</math> Getränkekisten übereinander gestapelt werden können. Also bleibt zu berechnen: <math>625\cdot 6=3750</math>. | |||
Insgesamt finden demnach <math>3750</math> Getränkekisten auf der Lagerfläche Platz. | |||
|2=Lösung zu b)|3=Lösung ausblenden}} | |||
| Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | |||
{{Box|Idee| | |||
Landwirt Mertens hat bisher eine quadratische Weide für seine paar Schafe. Da nun an dieser Stelle eine Landstraße ausgebaut werden soll, fragt die Stadt den Landwirt, ob er ein flächengleiches, rechteckiges Grundstück auf der anderen Seite seines Bauernhofes gegen seine quadratische Weide tauschen würde. Diese Weide ist zwar vier Meter kürzer, dafür aber sechs Meter länger. | |||
Landwirt Mertens überlegt: | |||
[[Datei:Weide Landwirt.png|Weide_Landwirt.png|600px]] | |||
# Hilf ihm und finde die Maße der Weiden heraus. Bearbeite diese Aufgabe in deinem Heft. Wenn du nicht weißt, wie du vorgehen sollst, schaue dir nach und nach die Tipps unten an. | |||
# Wie bist du vorgegangen, um die mathematische Gleichung zu lösen? Notiere deine Vorgehensweise im Heft.|Unterrichtsidee}} | |||
{{Lösung versteckt|1= '''Was ist gegeben?''' | |||
zwei flächengleiche Flächen (Quadrat und Rechteck) | |||
x = Seitenlänge der quadratischen Weide | |||
x - 4 = eine Seitenlänge der rechteckigen Weide (3m kürzer) | |||
x + 6 = andere Seitenlänge der rechteckigen Weide (5m länger) | |||
Versuche nun eine Gleichung aufzustellen.|2=Tipp 1|3=Tipp ausblenden}} | |||
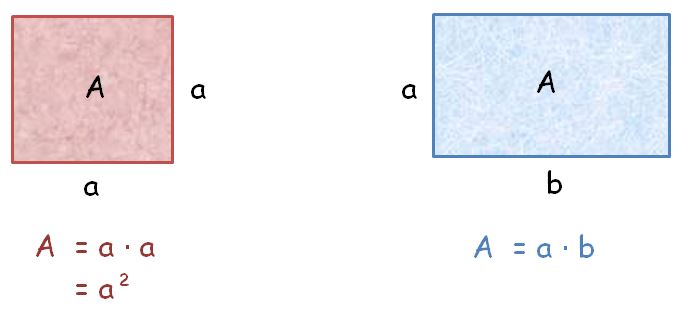
{{Lösung versteckt|1= Die beiden Weiden sind '''flächengleich''', d.h. ihr Flächeninhalt ist gleich. | |||
Benutze zum Aufstellen der Gleichung die Formeln für die Berechnung des '''Flächeninhaltes eines Quadrats und eines Rechtecks'''. | |||
[[Datei:Fläche Rechteck und Quadrat.jpg]] | |||
|2=Tipp 2|3=Tipp ausblenden}} | |||
{{Lösung versteckt|1= | |||
Beide Flächen sind gleich groß, daher lautet die Gleichung: | |||
'''x² = (x – 4) (x + 6) ''' | |||
Versuche nun x zu berechnen. Löse hierfür zunächst die Klammern auf. | |||
|2=Tipp 3|3=Tipp ausblenden}} | |||
{{Lösung versteckt|1= | |||
Du hast nun herausgefunden, dass die Länge und Breite der quadratischen Weide je 12m beträgt. | |||
Damit kannst du jetzt die '''Seitenlängen der rechteckigen Weide berechnen'''. Setze hierfür x = 12 in deine aufgestellten Terme ein: | |||
* x - 4 (eine Seitenlänge des Rechtecks) | |||
* x + 6 (andere Seitenlänge des Rechtecks) | |||
|2=Tipp 4|3=Tipp ausblenden}} | |||
Version vom 21. März 2023, 07:39 Uhr
In diesem Lernpfad geht es um das Vertiefen deines Wissens über Terme, Variablen und Gleichungen.
Du findest hier eine Wiederholung zu den Begriffen und Übungsaufgaben zu den Themen Terme aufstellen, Terme umformen und Gleichungen lösen. .
1.Terme, Variablen und Gleichungen
2.Terme
Terme aufstellen
Terme vereinfachen
a) =
b) =
c) =
d) =
e) =
f)
Klammern in Termen
Klammern auflösen: Das Ausmultiplizieren hat zum Ziel, eine Klammer aufzulösen.
Ausklammern Beim Ausklammern wird eine Summe in ein Produkt umgewandelt, es werden also Klammern hinzugefügt. Dies ist nur dann möglich, wenn die Summanden gemeinsame Faktoren haben.
3. Gleichungen
Vernetzte Aufgaben
Zahlenrätsel
Rechnen mit Gleichungen im Sachzusammenhang
Was ist gegeben?
zwei flächengleiche Flächen (Quadrat und Rechteck)
x = Seitenlänge der quadratischen Weide
x - 4 = eine Seitenlänge der rechteckigen Weide (3m kürzer)
x + 6 = andere Seitenlänge der rechteckigen Weide (5m länger)
Die beiden Weiden sind flächengleich, d.h. ihr Flächeninhalt ist gleich.
Benutze zum Aufstellen der Gleichung die Formeln für die Berechnung des Flächeninhaltes eines Quadrats und eines Rechtecks.
Beide Flächen sind gleich groß, daher lautet die Gleichung:
x² = (x – 4) (x + 6)
Versuche nun x zu berechnen. Löse hierfür zunächst die Klammern auf.Du hast nun herausgefunden, dass die Länge und Breite der quadratischen Weide je 12m beträgt. Damit kannst du jetzt die Seitenlängen der rechteckigen Weide berechnen. Setze hierfür x = 12 in deine aufgestellten Terme ein:
- x - 4 (eine Seitenlänge des Rechtecks)
- x + 6 (andere Seitenlänge des Rechtecks)