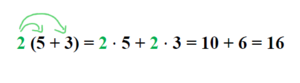Jule Volbers/Testseite: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 174: | Zeile 174: | ||
|3= Arbeitsmethode|Farbe={{Farbe|orange}}}} | |3= Arbeitsmethode|Farbe={{Farbe|orange}}}} | ||
{{Box|1 = Merke: Auflösen von Klammern|2 = Ergänze den Lückentext. Prüfe das Ergebnis und übertrage die Lösung in den Kasten "Klammern in Termen" in deinem Begleitheft. | |||
<div class="lueckentext-quiz"> | |||
Das Ausmultiplizieren hat zum Ziel, eine '''Klammer aufzulösen'''. Man multipliziert einen <span style="color: green">'''Faktor'''</span> mit einer Klammer, indem man den Faktor mit jedem einzelnen Glied in der Klammer '''multipliziert'''. <br /> | |||
<math> {\color{green}a}(b+c) = {\color{green}a}b + {\color{green}a}c</math>. | |||
Diese Regel nennt man '''Distributivgesetz'''. <br /> Es spielt keine Rolle, ob der Faktor links oder rechts von der Klammer steht: <br /> | |||
<math>(b+c) {\color{green}a} = b{\color{green}a} + c{\color{green}a} | |||
= {\color{green}a}b + {\color{green}a}c = {\color{green}a}(b+c) </math> <br /> | |||
Steht ein '''negativer Faktor''' vor der Klammer, '''drehen''' sich die Vorzeichen beim Auflösen der Klammer herum: | |||
- a(b - c) = '''-''' ab ''' + ''' ac'''. | |||
Zwei Summen (oder Differenzen) werden miteinander multipliziert, indem man '''jeden Summanden''' der ersten Klammer mit '''jedem Summanden''' der zweiten Klammer '''multipliziert:''' | |||
<math>(a+b)(c+d) = ac + ad + bc + bd</math>. | |||
</div> | |||
|3 = Merksatz}} | |||
{{Box|1=Merke: Auflösen von Klammern|2= Ergänze den Lückentext. Prüfe das Ergebnis und übertrage die Lösung in den Kasten "Klammern in Termen" in deinem Begleitheft. | {{Box|1=Merke: Auflösen von Klammern|2= Ergänze den Lückentext. Prüfe das Ergebnis und übertrage die Lösung in den Kasten "Klammern in Termen" in deinem Begleitheft. | ||
| Zeile 248: | Zeile 265: | ||
|3 = Merksatz}} | |3 = Merksatz}} | ||
{{Box|1 = Training: lineare Gleichungen lösen |2= Löse die Gleichungen. Führe, wenn möglich, eine Probe durch. Denke daran: Eine Probe kann nur durchgeführt werden, wenn es mindestens eine Lösung für die Gleichung gibt. | |||
'''a)''' <math>2a-64=5+a</math> | |||
{{Lösung versteckt|1=<math>\begin{align} & & a-64 &=5+a & &\mid +64\\ | |||
\Leftrightarrow & & a &=69 \\ | |||
\end{align}</math> | |||
Probe: | |||
<math>\begin{align} & & 69-64 &=5 \\ | |||
\Leftrightarrow & & 69-64 &=5\\ | |||
\Leftrightarrow & & 5 &=5 | |||
\end{align}</math> | |||
|2=Lösung|3=Lösung ausblenden}} | |||
'''b)''' <math>3x+7=16</math> | |||
{{Lösung versteckt|1=<math>\begin{align} & & 3x+7&=16 & &\mid -7\\ | |||
\Leftrightarrow & & 3x &=9 & &\mid :3\\ | |||
\Leftrightarrow & & x &=3\\ | |||
\end{align}</math> | |||
Probe: | |||
<math>\begin{align} & & 3\cdot 3+7&=16\\ | |||
\Leftrightarrow & & 9+7 &=16\\ | |||
\Leftrightarrow & & 16 &=16 | |||
\end{align}</math> | |||
|2=Lösung|3=Lösung ausblenden}} | |||
'''c)''' <math>4(x+1)-4x-5=1</math> | |||
{{Lösung versteckt|1=<math>\begin{align} & & 4(x+1)-4x-5 &=1\\ | |||
\Leftrightarrow & & 4x+4-4x-5 &=1\\ | |||
\Leftrightarrow & & 4x-4x+4-5 &=1\\ | |||
\Leftrightarrow & & -1 &=1 | |||
\end{align}</math> | |||
Das ist ein Widerspruch. Deshalb ist die Lösungsmenge leer: <math>\mathbb{L}=\{\}</math>. Hier ist keine Probe durch Einsetzen möglich, weil die Lösungsmenge leer ist. | |||
|2=Lösung|3=Lösung ausblenden}} | |||
'''d)''' <math>\frac{1}{2x}=0,5</math> | |||
{{Lösung versteckt|1=Versuche die Gleichung so umzustellen, dass du Brüche kürzen kannst.|2=Tipp|3=Tipp ausblenden}} | |||
{{Lösung versteckt|1=<math>\begin{align} & & \frac{1}{2x} &=0,5 & & \mid \cdot 2x\\ | |||
\Leftrightarrow & & \frac{1}{2x} \cdot 2x &= 0,5 \cdot 2x & & \mid \text{kürzen}\\ | |||
\Leftrightarrow & & 1 &=0,5\cdot 2x & & \mid :0,5\\ | |||
\Leftrightarrow & & \frac{1}{0,5} &=\frac{0,5}{0,5} \cdot 2x & & \mid \text{kürzen}\\ | |||
\Leftrightarrow & & 2 &=2x & &\mid :2\\ | |||
\Leftrightarrow & & 1 &=x\\ | |||
& & \mathbb{L}=\{1\} | |||
\end{align}</math> | |||
Probe: | |||
<math>\begin{align} & & \frac{1}{2 \cdot 1} &=0,5 & &\\ | |||
\Leftrightarrow & & \frac{1}{2} &=0,5 & &\\ | |||
\Leftrightarrow & & 0,5 &=0,5 | |||
\end{align}</math> | |||
|2=Lösung|3=Lösung ausblenden}} | |||
'''e)''' <math>d\cdot (d-5)=0</math> | |||
{{Lösung versteckt|1=Überlege dir, was für zwei Faktoren gilt, deren Produkt <math>0</math> ist.|2=Tipp |3=Tipp ausblenden}} | |||
{{Lösung versteckt|1=Ein Produkt ist dann <math>0</math>, wenn einer der Faktoren <math>0</math> ist. Deshalb kann man die Aufgabe so lösen: | |||
<math>\begin{align} & & d\cdot (d-5)&=0\\ | |||
\Leftrightarrow & & d=0 &\text{ oder } d-5=0\\ | |||
\Leftrightarrow & & d=0 &\text{ oder } d=5\\ | |||
& & \mathbb{L}=\{0,5\} | |||
\end{align}</math> | |||
Probe: | |||
<math>\begin{align} & & 0\cdot (0-5)&=0\\ | |||
\Leftrightarrow & & 0&=0 | |||
\end{align}</math> | |||
<math>\begin{align} & & 5\cdot (5-5)&=0\\ | |||
\Leftrightarrow & & 5\cdot 0&=0\\ | |||
\Leftrightarrow & & 0&=0 | |||
\end{align}</math> | |||
|2=Lösung|3=Lösung ausblenden}} | |||
Sprinteraufgabe: | |||
'''f)''' <math>\frac{3}{z+1}=-\frac{5}{2z-1}</math> | |||
{{Lösung versteckt|1=Versuche die Variablen mit Hilfe der Multiplikation aus dem Nenner zu bekommen.|2=Tipp|3=Tipp ausblenden}} | |||
{{Lösung versteckt|1=<math>\begin{align} & & \frac{3}{z+1} &= - \frac{5}{2z-1} & & \mid \cdot (z+1)\\ | |||
\Leftrightarrow & & \frac{3}{z+1} \cdot (z+1) &= - \frac{5 \cdot (z+1)}{2z-1} & & \mid \text{kürzen}\\ | |||
\Leftrightarrow & & 3 &= - \frac{5 \cdot (z+1)}{2z-1} & & \mid \cdot (2z-1)\\ | |||
\Leftrightarrow & & 3 \cdot (2z-1) &= - \frac{5 \cdot (z+1)}{2z-1} \cdot (2z-1) & & \mid \text{kürzen}\\ | |||
\Leftrightarrow & & 3 \cdot (2z-1) &= - 5 \cdot (z+1) & &\\ | |||
\Leftrightarrow & & 6z-3 &= -5z-5 & & \mid +5z\\ | |||
\Leftrightarrow & & 11z-3 &= -5 & & \mid +3\\ | |||
\Leftrightarrow & & 11z &= -2 & & \mid :11\\ | |||
\Leftrightarrow & & z &= - \frac{2}{11}\\ | |||
& & \mathbb{L}=\{-\frac{2}{11}\} | |||
\end{align}</math> | |||
Probe: | |||
<math>\begin{align} & & \frac{3}{- \frac{2}{11} +1} &= - \frac{5}{2 \cdot (- \frac{2}{11}) -1} & &\\ | |||
\Leftrightarrow & & \frac{3}{\frac{9}{11}} &= - \frac{5}{- \frac{4}{11} -1} & &\\ | |||
\Leftrightarrow & & \frac{3}{\frac{9}{11}} &= - \frac{5}{- \frac{15}{11}} & & \mid \text{mit dem Kehrwert mal nehmen}\\ | |||
\Leftrightarrow & & 3 \cdot \frac{11}{9} &= - 5 \cdot - \frac{11}{15} & &\\ | |||
\Leftrightarrow & & \frac{33}{9} &= \frac{55}{15} & & \mid \text{kürzen}\\ | |||
\Leftrightarrow & & \frac{11}{3} &= \frac{11}{3} | |||
\end{align}</math> | |||
|2=Lösung|3=Lösung ausblenden}} | |||
|Üben|Farbe={{Farbe|orange|heller}}}} | |||
{{Box | 1=Training: lineare Gleichungen lösen| | {{Box | 1=Training: lineare Gleichungen lösen| | ||
| Zeile 360: | Zeile 492: | ||
| 3=Arbeitsmethode | Farbe={{Farbe|orange}} }} | | 3=Arbeitsmethode | Farbe={{Farbe|orange}} }} | ||
Quadratische Gleichungen lösen. Auch für die Lösung quadratischer Gleichungen hast du Verfahren kennengelernt. Die Aufgaben helfen dir dabei, diese zu wiederholen. | |||
{{Box|q = Einfache quadratische Gleichungen|2= | |||
Löse die quadratischen Gleichungen '''ohne p-q-Formel'''. | |||
a) <math>0=x^2-64</math> | |||
b) <math>0=x^2+13x</math> | |||
c) <math>-2x=\frac{1}{2}x^2</math> | |||
{{Lösung versteckt|1=zu a): Bei Gleichungen der Form <math>ax^2+c</math>, also ohne linearen Summanden <math>bx</math> kannst du die Gleichung umstellen, sodass <math>x^2</math> alleine steht und anschließend die Wurzel ziehen.|2=Tipp 1|3=schließen}} | |||
{{Lösung versteckt|1=zu a): Achte beim Wurzelziehen auf die positive und negative Lösung.|2=Tipp 2|3=schließen}} | |||
{{Lösung versteckt|1=zu b): Bei Gleichungen der Form <math>ax^2+bx</math>, also ohne konstanten Summanden <math>c</math> kannst du <math>x</math> ausklammern.|2=Tipp 3|3=schließen}} | |||
{{Lösung versteckt|1=zu b): Ein Produkt ist genau dann <math>0</math>, wenn einer der beiden Faktoren bereits <math>0</math> ist. ''Beispiel:'' <math>{\color{blue}x} \cdot ({\color{red}x-2})=0</math> bedeutet, dass entweder <math>{\color{blue}x}=0</math> oder <math>{\color{red}x-2}=0</math> gilt.|2=Tipp 4|3=schließen}} | |||
{{Lösung versteckt|1=zu c): Stelle um, sodass auf einer Seite des Gleichheitszeichen <math>0</math> steht.|2=Tipp 5|3=schließen}} | |||
{{Lösung versteckt|1= | |||
zu a) | |||
<math> | |||
\begin{alignat}{3} | |||
& & 0 &= x^2-64 \qquad &&| +64\\ | |||
&\Leftrightarrow \qquad & 64 &= x^2 &&| \sqrt{\text{ }}\\ | |||
&\Leftrightarrow &\pm 8 &= x &&\\ | |||
&\Leftrightarrow & x_1 &= -8 \text{ oder } x_2=8&& | |||
\end{alignat} | |||
</math> | |||
zu b) | |||
<math> | |||
\begin{alignat}{5} | |||
& & & & 0 &= x^2+13x & & &&| x \text{ ausklammern}\\ | |||
&\Leftrightarrow \qquad & & & 0 &= x \cdot (x+13) & & &&| \text{einer der beiden Faktoren muss } 0 \text{ sein}\\ | |||
&\Leftrightarrow & 0 &= x_1 \qquad & \text{ o}&\text{der } & 0 &= x_2+13 \qquad &&|-13\\ | |||
&\Leftrightarrow & 0 &= x_1 & \text{ o}&\text{der } & -13 &= x_2 &&\\ | |||
&\Leftrightarrow & x_1 &= 0 & \text{ o}&\text{der } & x_2 &= -13 && | |||
\end{alignat} | |||
</math> | |||
zu c) | |||
<math> | |||
\begin{alignat}{5} | |||
& & & & -2x &= \frac{1}{2}x^2 & & &&| +2x\\ | |||
&\Leftrightarrow \qquad & & & 0 &= \frac{1}{2}x^2+2x & & &&| \cdot 2\\ | |||
&\Leftrightarrow & & & 0 &= x^2+4x & & &&| x \text{ ausklammern}\\ | |||
&\Leftrightarrow & & & 0 &= x \cdot (x+4) & & &&| \text{einer der beiden Faktoren muss } 0 \text{ sein}\\ | |||
&\Leftrightarrow & 0 &= x_1 \qquad & \text{ o}&\text{der } & 0 &= x_2+4 \qquad &&|-4\\ | |||
&\Leftrightarrow & 0 &= x_1 & \text{ o}&\text{der } & -4 &= x_2 &&\\ | |||
&\Leftrightarrow & x_1 &= 0 & \text{ o}&\text{der } & x_2 &= -4 && | |||
\end{alignat} | |||
</math>}} | |||
|Arbeitsmethode|Farbe={{Farbe|orange}}}} | |||
{{Box|1=15. Einfache quadratische Gleichungen|2= | {{Box|1=15. Einfache quadratische Gleichungen|2= | ||
| Zeile 415: | Zeile 601: | ||
{{Box|1=16. Quadratische Gleichungen mit Standardverfahren|2= | {{Box|1=16. Quadratische Gleichungen mit Standardverfahren|2= | ||
Löse die quadratischen Gleichungen. | Löse die quadratischen Gleichungen. | ||
a) <math>0=x^2+12x+27</math> | a) <math>0=x^2+12x+27</math> | ||
Version vom 21. März 2023, 07:06 Uhr
In diesem Lernpfad geht es um das Vertiefen deines Wissens über Terme, Variablen und Gleichungen.
Du findest hier eine Wiederholung zu den Begriffen und Übungsaufgaben zu den Themen Terme aufstellen, Terme umformen und Gleichungen lösen. .
1.Terme, Variablen und Gleichungen
2.Terme
Terme aufstellen
Terme vereinfachen
a) =
b) =
c) =
d) =
e) =
f)
Klammern in Termen
Klammern auflösen: Das Ausmultiplizieren hat zum Ziel, eine Klammer aufzulösen.
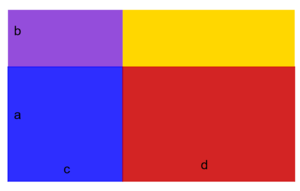
Ausklammern Beim Ausklammern wird eine Summe in ein Produkt umgewandelt, es werden also Klammern hinzugefügt. Dies ist nur dann möglich, wenn die Summanden gemeinsame Faktoren haben.
3. Gleichungen
Lineare Gleichungen lösen
Quadratische Gleichungen lösen. Auch für die Lösung quadratischer Gleichungen hast du Verfahren kennengelernt. Die Aufgaben helfen dir dabei, diese zu wiederholen.