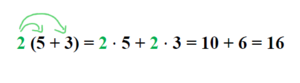|
|
| Zeile 47: |
Zeile 47: |
| {{Box|Info|Terme enthalten unterschiedliche Rechenoperationen wie Addition, Subtraktion, Multiplikation und Division. Manche Teile von Termen kann man zusammenfassen, um so den Term zu vereinfachen. Du hast die Regeln im Unterricht bereits kennengelernt.|Kurzinfo||Farbe={{Farbe|sekundär-1|x-heller}}}} | | {{Box|Info|Terme enthalten unterschiedliche Rechenoperationen wie Addition, Subtraktion, Multiplikation und Division. Manche Teile von Termen kann man zusammenfassen, um so den Term zu vereinfachen. Du hast die Regeln im Unterricht bereits kennengelernt.|Kurzinfo||Farbe={{Farbe|sekundär-1|x-heller}}}} |
|
| |
|
| | {{Box|Übung 5 Zur Erinnerung: Überflüssige Malpunkte|Um Produktterme so einfach wie möglich zu schreiben, dürfen überflüssige Malpunkte weggelassen werden. Dies sind Malpunkte zwischen einer Zahl und einer Variablen und zwischen einer Zahl oder Variablen und einer Klammer.Markiere die überflüssigen Malpunkte in den Termen.|Üben}} |
| | {{LearningApp|app=pynxyt0qk20|width=100%|height=300px}} |
| | |
| | {{Box|Info|Überflüssige Malpunkte werden nicht notiert. |Kurzinfo||Farbe={{Farbe|sekundär-1|x-heller}}}} |
| {{Box|Terme zusammenfassen| | | {{Box|Terme zusammenfassen| |
| Vereinfache die Terme soweit wie möglich. Wenn du dir unsicher bist, schaue dir die Tipps an. <br/> | | Vereinfache die Terme soweit wie möglich. Wenn du dir unsicher bist, schaue dir die Tipps an. <br/> |
Version vom 20. März 2023, 07:27 Uhr
Willkommen auf dem Lernpfad: Nützliche Werkzeuge - Terme und Gleichungen.
In diesem Lernpfad geht es um das Vertiefen deines Wissens über Terme, Variablen und Gleichungen.
Du findest hier eine Wiederholung zu den Begriffen und Übungsaufgaben zu den Themen Terme aufstellen, Terme umformen und Gleichungen lösen. .
1.Terme, Variablen und Gleichungen
Was ist Was?" - Wiederhole die Begriffe!
Ergänze den Lückentext. Prüfe das Ergebnis und übertrage die Lösung in den Kasten "Terme, Variablen und Gleichungen" in deinem Begleitmaterial.
Variablen sind Zeichen (meistens kleine Buchstaben). Sie sind Platzhalter. Du kannst Zahlen für sie einsetzen. Terme sind Rechenausdrücke. Terme können Zahlen, Rechenzeichen, Klammern und Variable enthalten. Werden zwei Terme mit einem Gleichheitszeichen verbunden, entsteht eine Gleichung. Es gibt verschiedene Arten von Gleichungen. Wichtige Arten sind die linearen und die quadratischen Gleichungen.
2.Terme
Terme aufstellen
Terme in Sachsituationen
Du hast gelernt, Sachsituationen mit Hilfe von Termen zu beschreiben. Hier kannst du dein Wissen testen.
a)
b)
Terme vereinfachen
Info
Terme enthalten unterschiedliche Rechenoperationen wie Addition, Subtraktion, Multiplikation und Division. Manche Teile von Termen kann man zusammenfassen, um so den Term zu vereinfachen. Du hast die Regeln im Unterricht bereits kennengelernt.
Übung 5 Zur Erinnerung: Überflüssige Malpunkte
Um Produktterme so einfach wie möglich zu schreiben, dürfen überflüssige Malpunkte weggelassen werden. Dies sind Malpunkte zwischen einer Zahl und einer Variablen und zwischen einer Zahl oder Variablen und einer Klammer.Markiere die überflüssigen Malpunkte in den Termen.
Info
Überflüssige Malpunkte werden nicht notiert.
Idee
Wichtig: Unterscheide


Beachte außerdem: Punkt- vor Strichrechnung, die Klammer geht immer vor.
Termtraining.
Füge die zugehörigen Terme zusammen. Du kannst hierfür deinen Stift und Papier nutzen.
Klammern in Termen
Klammern auflösen:
Das Ausmultiplizieren hat zum Ziel, eine Klammer aufzulösen.
Arbeitsmethode
a) Erkläre mit Hilfe der Abbildung, dass für das Auflösen von Klammern gilt:
 .
.
 .
Formuliere die Regel in eigenen Worten. Wende sie auf das Beispiel a = 2, b = 5 und c = 3 an. Kontrolliere dann deine Lösung.
.
Formuliere die Regel in eigenen Worten. Wende sie auf das Beispiel a = 2, b = 5 und c = 3 an. Kontrolliere dann deine Lösung.
Man multipliziert einen Faktor mit einer Klammer, indem man den Faktor mit jedem einzelnen Glied in der Klammer multipliziert.
Es spielt keine Rolle, ob der Faktor links oder rechts von der Klammer steht:
 .
.
Erinnerung
- Achte darauf, ob in der Klammer eine Summe oder Differenz steht, denn:

- Bei Minusklammern, also wenn vor der Klammer ein negativer Faktor steht, drehen sich die Vorzeichen von jedem Glied in der Klammer um:
 .
.
 .
.
b)
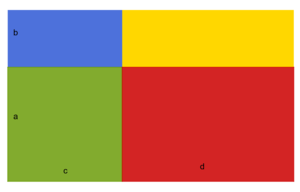
Erkläre mit Hilfe der Abbildung, dass für die Multiplikation zweier Summen oder Differenzen folgende Regel gilt:
 . Erkläre die Regel in eigenen Worten und wende sie auf das Beispiel a = 2, b = 3, c = 7 und d = -2 an. Kontrolliere dann deine Lösung
. Erkläre die Regel in eigenen Worten und wende sie auf das Beispiel a = 2, b = 3, c = 7 und d = -2 an. Kontrolliere dann deine Lösung
Zwei Summen (oder Differenzen) werden miteinander multipliziert, indem man jeden Summanden der ersten Klammer mit jedem Summanden der zweiten Klammer multipliziert:
Erinnerung: Es gilt:
 ergibt:
ergibt: 
 ergibt:
ergibt: 
 ergibt:
ergibt: 
 .
.
 .
.
 .
.

.
Klammern in Termen
Ergänze den Lückentext. Prüfe das Ergebnis und übertrage die Lösung in den Kasten "Klammern in Termen" in deinem Begleitmaterial.
Das Ausmultiplizieren hat zum Ziel, eine Klammer aufzulösen. Man multipliziert einen Faktor mit einer Klammer, indem man den Faktor mit jedem einzelnen Glied in der Klammer multipliziert.
 .
Dies nennt man Distributivgesetz.
.
Dies nennt man Distributivgesetz.
Es spielt keine Rolle, ob der Faktor links oder rechts von der Klammer steht:
 .
Zwei Summen (oder Differenzen) werden miteinander multipliziert, indem man jeden Summanden der ersten Klammer mit jedem Summanden der zweiten Klammer multipliziert:
.
Zwei Summen (oder Differenzen) werden miteinander multipliziert, indem man jeden Summanden der ersten Klammer mit jedem Summanden der zweiten Klammer multipliziert:
 .
.
Aufgabe
Aufgabe 1: Zuordnen
In dieser Aufgabe kannst du das Ausmultiplizieren üben. Ordne jedem Klammerterm die richtige ausmultiplizierte Lösung zu. Nimm dir einen Zettel für Nebenrechnungen zur Hilfe.
Klammern auflösen
Ausklammern
3. Gleichungen
Vernetzte Aufgaben