Informatik am Gymnasium Trittau/Digitale Informationsverarbeitung/Volladdierer: Unterschied zwischen den Versionen
GT044 (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
GT044 (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
== | ===Allgemeine Informationen=== | ||
Mit Hilfe eines Volladdierers können drei einstellige Binärzahlen addiert werden. | Mit Hilfe eines Volladdierers können drei einstellige Binärzahlen addiert werden. | ||
| Zeile 9: | Zeile 8: | ||
Beispielsweise kann man so einen Volladdierer mit dem Programm [https://github.com/hneemann/Digital|Digital|] erstellen. | Beispielsweise kann man so einen Volladdierer mit dem Programm [https://github.com/hneemann/Digital|Digital|] erstellen. | ||
<br /> | |||
===Funktionsweise=== | ===Funktionsweise=== | ||
[[Datei:Volladdierer .png|mini| | [[Datei:Volladdierer .png|mini|604.4x604.4px|alternativtext=|zentriert]] | ||
| Zeile 18: | Zeile 18: | ||
<br /> | <br /> | ||
[[Datei:Schaltung für 2^1.png|mini| | [[Datei:Schaltung für 2^1.png|mini|595x595px|alternativtext=|zentriert]] | ||
| Zeile 26: | Zeile 26: | ||
<br /> | <br /> | ||
[[Datei:Schaltung für 2^0.png|mini| | [[Datei:Schaltung für 2^0.png|mini|598x598px|alternativtext=|zentriert]] | ||
| Zeile 34: | Zeile 34: | ||
<br /> | <br /> | ||
[[Datei:Schaltung für 2^0 und 2^1.png|mini| | [[Datei:Schaltung für 2^0 und 2^1.png|mini|619.2x619.2px|alternativtext=|zentriert]] | ||
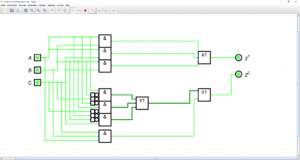
Die 2^0 und 2^1 stehen für die Binärzahl 1 1. Wenn nun alle drei Eingänge ein Signal geben, werden sowohl alle oberen UND-Schaltungen, als auch die eine untere UND-Schaltung aktiviert. Dadurch werden beide Ausgänge aktiviert. | Die 2^0 und 2^1 stehen für die Binärzahl 1 1. Wenn nun alle drei Eingänge ein Signal geben, werden sowohl alle oberen UND-Schaltungen, als auch die eine untere UND-Schaltung aktiviert. Dadurch werden beide Ausgänge aktiviert. | ||
Version vom 7. Dezember 2022, 15:01 Uhr
Allgemeine Informationen
Mit Hilfe eines Volladdierers können drei einstellige Binärzahlen addiert werden.
Benötigt werden dafür drei Eingänge und zwei Ausgänge, da im Binärsystem eine 3 (größtmögliche Zahl bei drei Eingängen) einer 1 1 entspricht.
Beispielsweise kann man so einen Volladdierer mit dem Programm [1] erstellen.
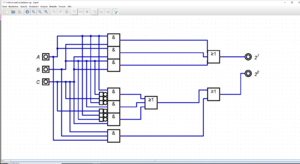
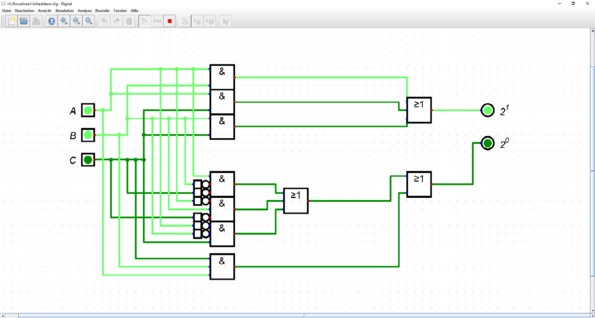
Funktionsweise
Ein Volladdierer mit A, B und C Eingängen, sowie 2^0 und 2^1 Ausgängen.
Die 2^1 steht für die Binärzahl 1 0. Wenn nun zwei beliebeige Eingänge ein Signal geben, wird eine der oberen UND-Schaltungen aktiviert und ein Ausgangssignal an die obere ODER-Schaltung weitergeleitet. Die ODER-Schaltung aktiviert dann den entsprechenden Ausgang.
Die 2^0 wird nicht aktiviert, da entweder die untere UND-Schaltung durch alle Signale aktiviert werden muss, oder eine der UND-Schaltungen in Verbindung mit den jeweils zwei NICHT-Schaltungen davor aktiviert sein muss.
Die 2^0 steht für die Binärzahl 0 1. Wenn nun ein beliebiger Eingang ein Signal gibt, wird eine der UND-Schaltungen in Verbindung mit den jeweils zwei NICHT-Schaltungen aktiviert und ein Signal wird an die untere ODER-Schaltung weitergegeben. Die ODER-Schaltung aktiviert dann den entsprechenden Ausgang.
Die 2^1 wird nicht aktiviert, da mindestens zwei Eingänge ein Signal an die oberen UND-Schaltungen liefern müssen, damit diese aktiviert werden.
Die 2^0 und 2^1 stehen für die Binärzahl 1 1. Wenn nun alle drei Eingänge ein Signal geben, werden sowohl alle oberen UND-Schaltungen, als auch die eine untere UND-Schaltung aktiviert. Dadurch werden beide Ausgänge aktiviert.