Benutzer:Buss-Haskert/Quadratische Funktionen: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
K (Tabelle) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 156: | Zeile 156: | ||
===Die gestreckte und gestauchte Parabel: Bedeutung des Parameters''' a''' in f(x) = '''a'''x²=== | ===Die gestreckte und gestauchte Parabel: Bedeutung des Parameters''' a''' in f(x) = '''a'''x²=== | ||
Link zum Applet (falls es nicht vollständig dargestellt wird):[https://www.geogebra.org/m/kAmAHEzU] | |||
<ggb_applet id="UEdR9CNz" width="1890" height="839" border="888888" /> | |||
Applet von G.von Lechberg<br> | |||
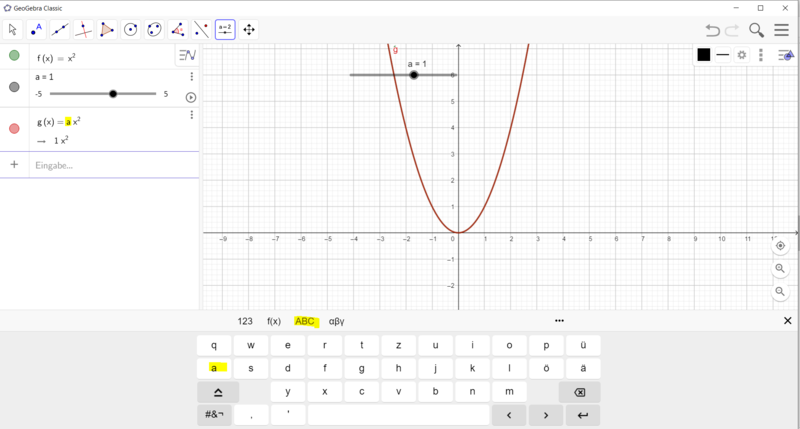
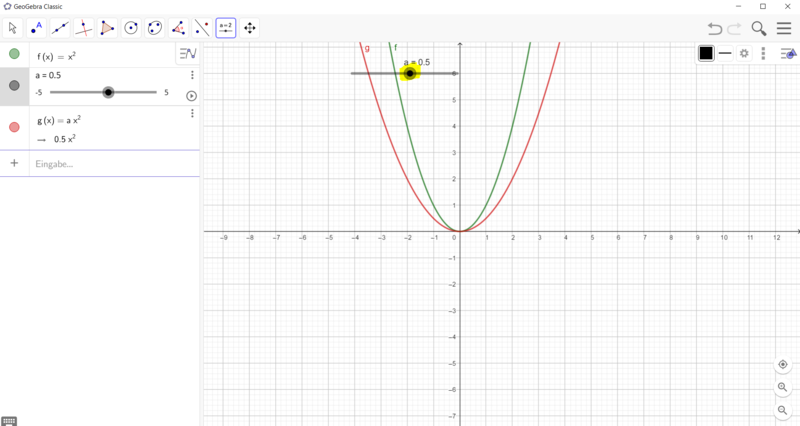
{{Box|1=f(x) = ax² Bedeutung des Parameters a|2= Untersuche die Bedeutung des Parameters a in der Gleichung f(x) = ax² mithilfe der Geometriesoftware GeoGebra. | {{Box|1=f(x) = ax² Bedeutung des Parameters a|2= Untersuche die Bedeutung des Parameters a in der Gleichung f(x) = ax² mithilfe der Geometriesoftware GeoGebra. | ||
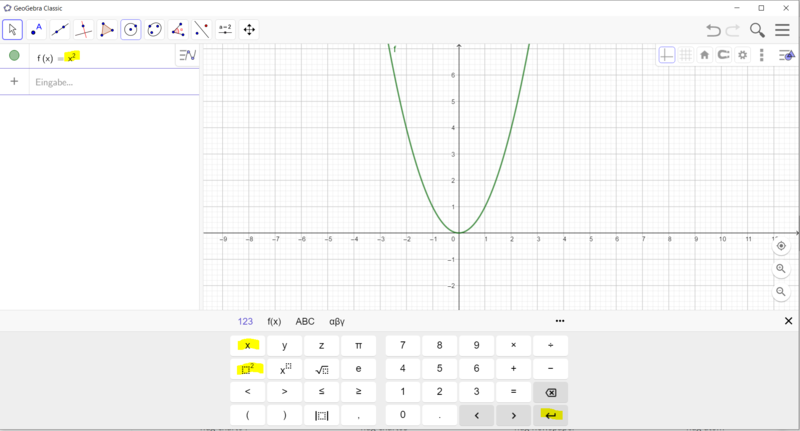
* Gib im Algebrafenster die Gleichung f(x) = x² ein. Es wird die Normalparabel gezeichnet. | * Gib im Algebrafenster die Gleichung f(x) = x² ein. Es wird die Normalparabel gezeichnet. | ||
| Zeile 169: | Zeile 173: | ||
[[Datei:GeoGebra Funktionsgleichung mit Schieberegler.png|rahmenlos|800x800px]]<br> | [[Datei:GeoGebra Funktionsgleichung mit Schieberegler.png|rahmenlos|800x800px]]<br> | ||
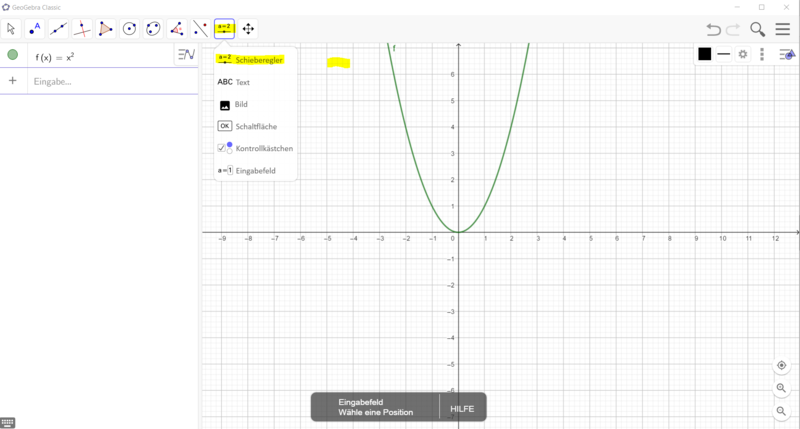
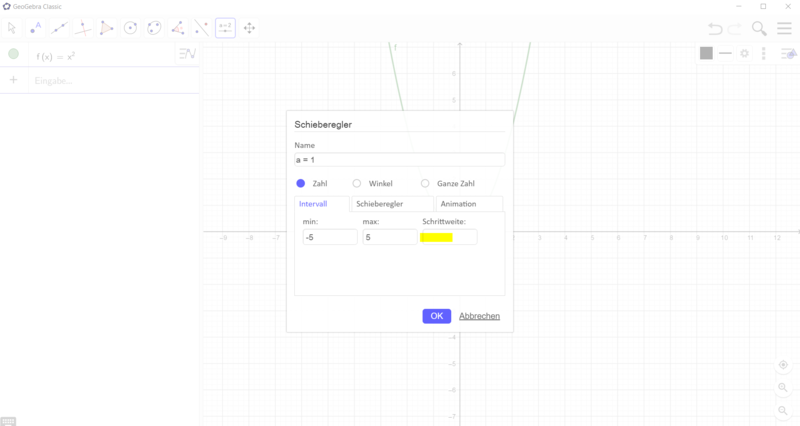
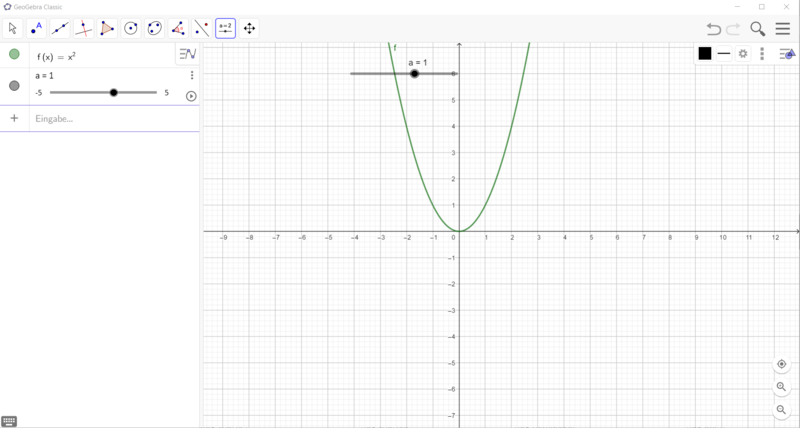
[[Datei:GeoGebra Schieberegler a verändern.png|rahmenlos|800x800px]]|2=Wie erstelle ich einen Schieberegler für die Funktionsgleichung f(x) = ax²?|3=Verbergen}} | [[Datei:GeoGebra Schieberegler a verändern.png|rahmenlos|800x800px]]|2=Wie erstelle ich einen Schieberegler für die Funktionsgleichung f(x) = ax²?|3=Verbergen}} | ||
{{Box|1=f(x) = ax² Bedeutung des Parameters a|2=Erstelle nun eine Wertetabelle zu den verschiedenen Funktionsgleichungen und zeichne die Parabeln in ein Koordinatenkreuz in dein Heft. Notiere die Bedeutung des Parameters a für den Verlauf der Parabel.<br> | |||
{{(!}} class=wikitable | |||
{{!-}} | |||
{{!}} x | |||
{{!}} -2 | |||
{{!}} -1 | |||
{{!}} -0,5 | |||
{{!}} 0 | |||
{{!}} 0,5 | |||
{{!}} 1 | |||
{{!}} 2 | |||
{{!}} Öffnung | |||
{{!}} Form | |||
{{!-}} | |||
{{!}} f(x) = x² | |||
{{!}} 4 | |||
{{!}} 1 | |||
{{!}} 0,25 | |||
{{!}} 0 | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} nach oben | |||
{{!}} Normalparabel | |||
{{!-}} | |||
{{!}} f(x) = 2x² | |||
{{!}} 8 | |||
{{!}} 2 | |||
{{!}} 0,5 | |||
{{!}} 0 | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} nach oben | |||
{{!}} gestreckt | |||
{{!-}} | |||
{{!}} f(x) = <math>\tfrac{1}{2}</math>x² | |||
{{!}} 2 | |||
{{!}} 0,5 | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} gestaucht | |||
{{!-}} | |||
{{!}} f(x) = -x² | |||
{{!}} -4 | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!-}} | |||
{{!}} f(x) = -2x² | |||
{{!}} -8 | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!-}} | |||
{{!}} f(x) = -<math>\tfrac{1}{2}</math>x² | |||
{{!}} -2 | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!)}}<br> | |||
Verwende verschiedene Farben.|Arbeitsmethode}} | |||
Version vom 28. Juni 2021, 15:46 Uhr
SEITE IM AUFGBAU
Mögliche Fragen könnten sein:
- In welcher Höhe wird der Ball abgeworfen?
- Wie hoch fliegt der Ball maximal?
- Wie weit fliegt der Ball?
| Frage | Mathematik |
| In welcher Höhe wird der Ball abgeworfen? | Schnittpunkt mit der y-Achse, y-Achsenabschnitt
x = 0 |
| Wie hoch fliegt der Ball maximal? | Scheitelpunkt S (d|e) |
| Wie weit fliegt der Ball? | Nullstelle
y = 0 |
Die Flugkurven haben alle eine Gemeinsamkeit. Ihre Form nennt man Parabel. Sie sind die Graphen/Schaubilder quadratischer Funktionen.
(auch als kahoot!)
Link zum Applet (falls es nicht vollständig dargestellt wird): [1]

Applet von C. Buß-Haskert
Link zum Applet (falls es nicht vollständig dargestellt wird): [2]

Applet von Bobby Knurek
Link zum Applet (falls es nicht vollständig dargestellt wird):[3] br>

Applet von Luc Morth
Link zum Applet (falls es nicht vollständig dargestellt wird):[4]

Applet von G.von Lechberg
Nun gilt es, die Bedeutung der Parameter a, d und e bzw. b und c zu erarbeiten!
Dazu beginnen wir mit der einfachsten Form der quadratischen Funktion, nämlich für a=1; d=0 und e=0 bzw. b=0 und c=0.
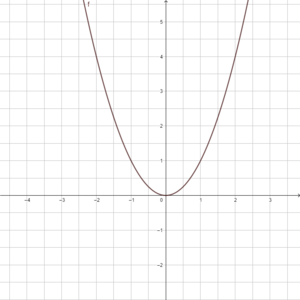
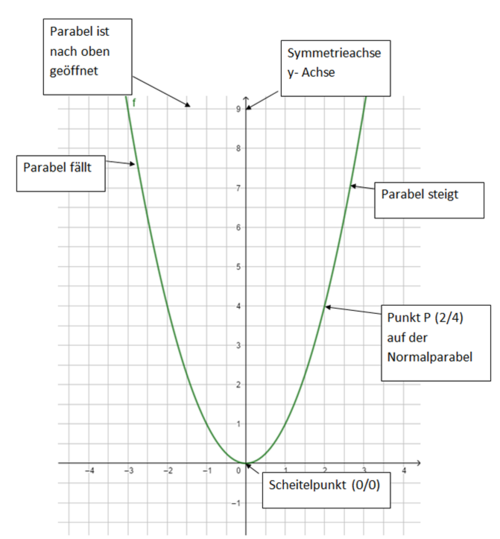
Diese Gleichung lautet f(x) = x².
Die Normalparabel
Erinnerung: (-2)² = (-2)·(-2) = +4
(Falls du später den Taschenrechner benutzt, denke an die Klammer, falls die Zahl ein Minuszeichen als Vorzeichen hat.)
Fülle den Lückentext aus.
Du kannst mithilfe des Schaubildes (Normalparabel) entscheiden, welche Punkte auf der Normalparabel liegen und welche nicht:
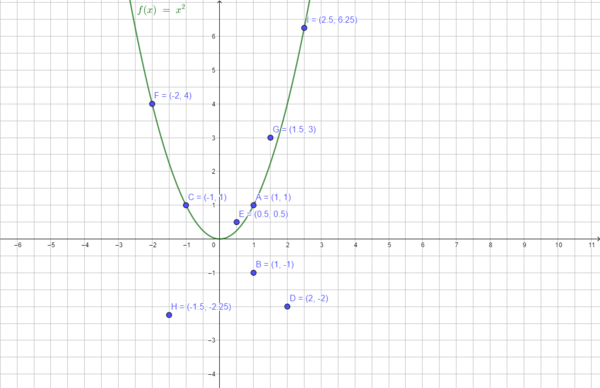
Wie kannst du rechnerisch prüfen, ob ein Punkt auf der Normalparabel liegt oder nicht?
Beispiel:
Liegt der Punkt I(2,5|6,25) auf der Normalparabel?
f(x) = x²
6,25 = 2,5²
6,25 = 6,25 (w), also liegt der Punkt I auf der Normalparabel.
Liegt der Punkt H(-1,5|-2,25) auf der Normalparabel?
f(x) = x²
-2,25 = (-1,5)²
-2,25 = 2,25 (f), also liegt der Punkt H nicht auf der Normalparabel.
Beispiel:
Bestimme die fehlende Koordinate von P(6|__) auf der Normalparabel.
f(x) = x²
y = 6²
y = 36, also P(6|36)
Bestimme die fehlende Koordinate von Q(__|1,69) auf der Normalparabel.
f(x) = x²
1,69 = x² |
= x
1,3 = x1; -1,3 = x2, also lautet Q1(1,3|1,69) und Q2(-1,3|1,69).
Es gibt zwei Punkte, die den y-Wert 1,69 haben, denn die Normalparabel ist symmetrisch zur y-Achse.
Die gestreckte und gestauchte Parabel: Bedeutung des Parameters a in f(x) = ax²
Link zum Applet (falls es nicht vollständig dargestellt wird):[5]

Applet von G.von Lechberg
Wie erstelle ich einen Schieberegler für die Funktionsgleichung f(x) = ax²?
Gehe vor, wie in den Bildern beschrieben: