Benutzer:Buss-Haskert/Quadratische Funktionen: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 122: | Zeile 122: | ||
{{Lösung versteckt|1=Wie erstelle ich einen Schieberegler für die Funktionsgleichung f(x) = ax²?<br> | {{Lösung versteckt|1=Wie erstelle ich einen Schieberegler für die Funktionsgleichung f(x) = ax²?<br> | ||
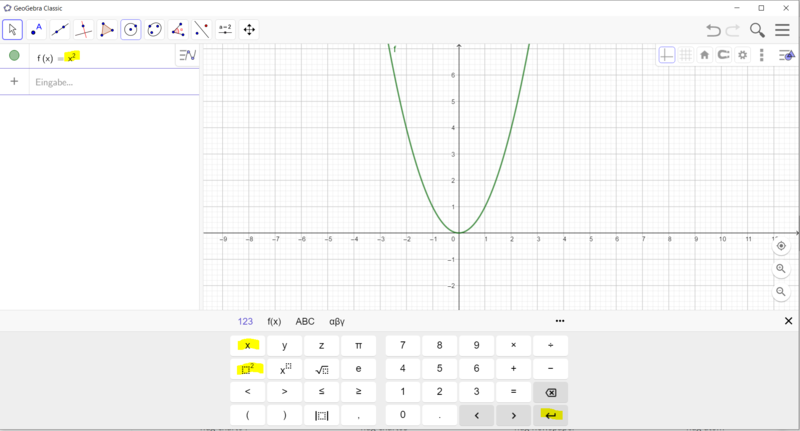
Gehe vor, wie in den Bildern beschrieben:<br> | Gehe vor, wie in den Bildern beschrieben:<br> | ||
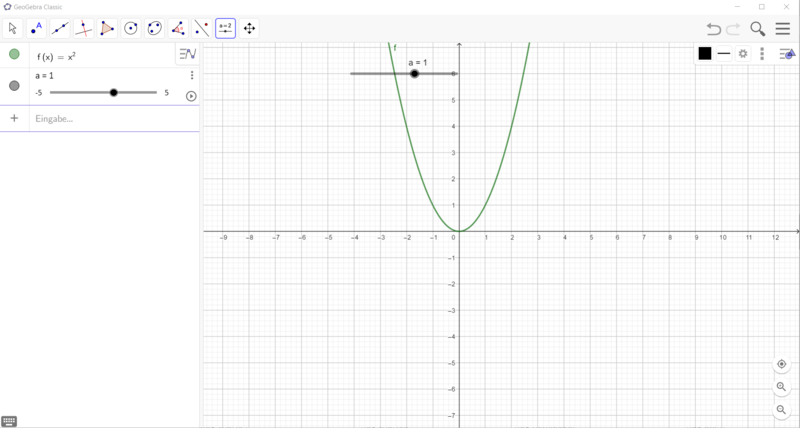
[[Datei:GeoGebra Normalparabel zeichnen.png|rahmenlos| | [[Datei:GeoGebra Normalparabel zeichnen.png|rahmenlos|800x800px]]<br> | ||
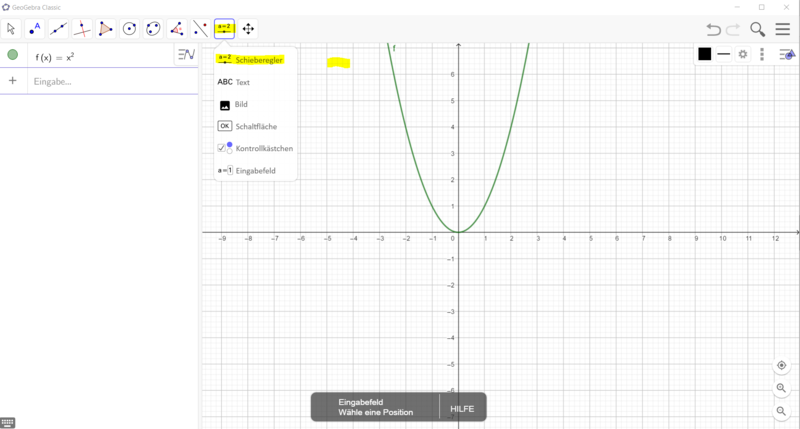
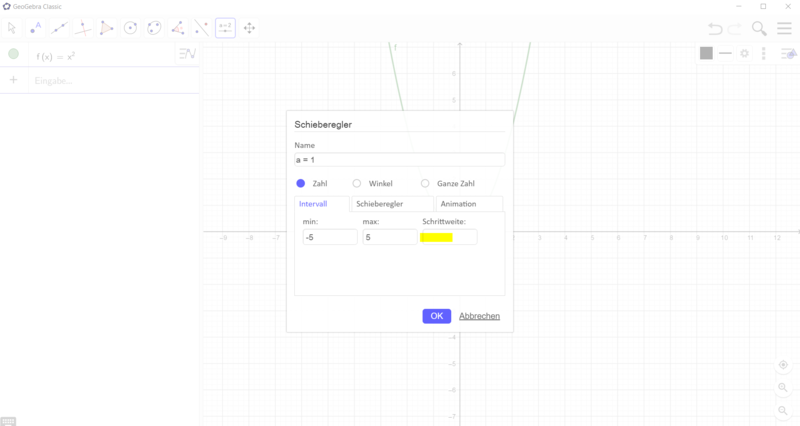
[[Datei:GeoGebra Schieberegler a erstellen.png|rahmenlos| | [[Datei:GeoGebra Schieberegler a erstellen.png|rahmenlos|800x800px]]<br> | ||
[[Datei:GeoGebra Schieberegler Schrittweite.png|rahmenlos| | [[Datei:GeoGebra Schieberegler Schrittweite.png|rahmenlos|800x800px]]<br> | ||
[[Datei:Geogebra Schieberegler fertig.png|rahmenlos| | [[Datei:Geogebra Schieberegler fertig.png|rahmenlos|800x800px]]<br> | ||
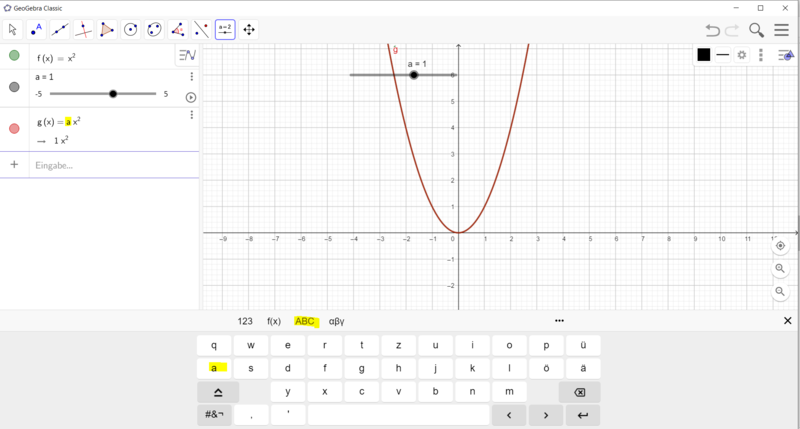
[[Datei:GeoGebra Funktionsgleichung mit Schieberegler.png|rahmenlos| | [[Datei:GeoGebra Funktionsgleichung mit Schieberegler.png|rahmenlos|800x800px]]<br> | ||
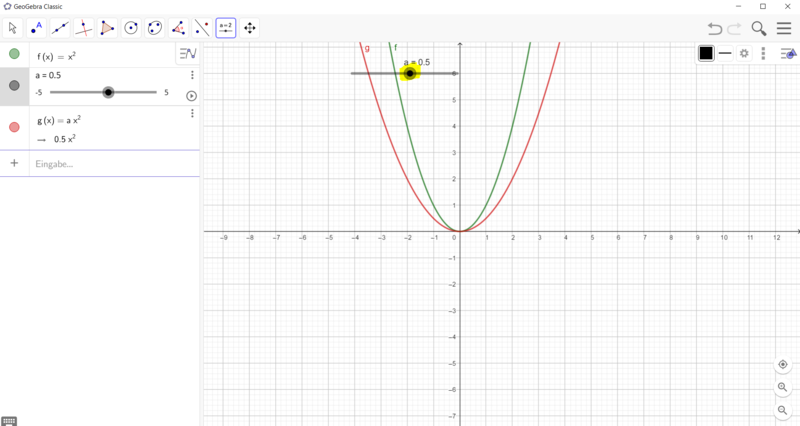
[[Datei:GeoGebra Schieberegler a verändern.png|rahmenlos| | [[Datei:GeoGebra Schieberegler a verändern.png|rahmenlos|800x800px]]|2=Wie erstelle ich einen Schieberegler für die Funktionsgleichung f(x) = ax²?|3=Verbergen}} | ||
Version vom 28. Juni 2021, 14:45 Uhr
SEITE IM AUFGBAU
Mögliche Fragen könnten sein:
- In welcher Höhe wird der Ball abgeworfen?
- Wie hoch fliegt der Ball maximal?
- Wie weit fliegt der Ball?
| Frage | Mathematik |
| In welcher Höhe wird der Ball abgeworfen? | Schnittpunkt mit der y-Achse, y-Achsenabschnitt
x = 0 |
| Wie hoch fliegt der Ball maximal? | Scheitelpunkt S (d|e) |
| Wie weit fliegt der Ball? | Nullstelle
y = 0 |
Die Flugkurven haben alle eine Gemeinsamkeit. Ihre Form nennt man Parabel. Sie sind die Graphen/Schaubilder quadratischer Funktionen.
(auch als kahoot!)
Link zum Applet (falls es nicht vollständig dargestellt wird): [1]

Applet von C. Buß-Haskert
Link zum Applet (falls es nicht vollständig dargestellt wird): [2]

Applet von Bobby Knurek
Link zum Applet (falls es nicht vollständig dargestellt wird):[3] br>

Applet von Luc Morth
Link zum Applet (falls es nicht vollständig dargestellt wird):[4]

Applet von G.von Lechberg
Nun gilt es, die Bedeutung der Parameter a, d und e bzw. b und c zu erarbeiten!
Dazu beginnen wir mit der einfachsten Form der quadratischen Gleichung, nämlich für a=1; d=0 und e=0 bzw. b=0 und c=0.
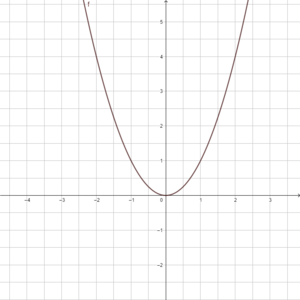
Diese Gleichung lautet f(x) = x².
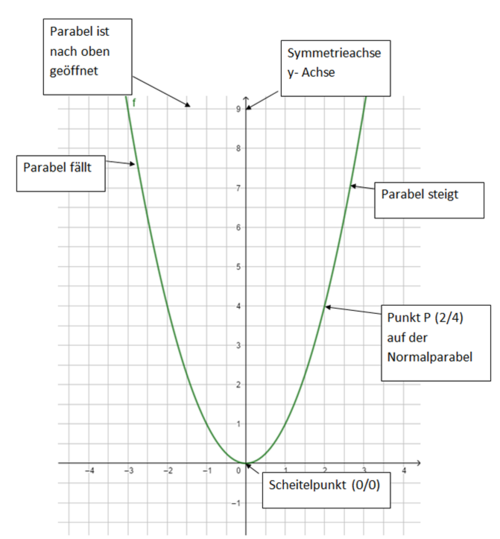
Die Normalparabel
Erinnerung: (-2)² = (-2)·(-2) = +4
(Falls du später den Taschenrechner benutzt, denke an die Klammer, falls die Zahl ein Minuszeichen als Vorzeichen hat.)
Fülle den Lückentext aus.