Benutzer:Buss-Haskert/Quadratische Funktionen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 56: | Zeile 56: | ||
Applet von Bobby Knurek<br> | Applet von Bobby Knurek<br> | ||
Link zum Applet (falls es nicht vollständig dargestellt wird):[https://www.geogebra.org/m/xqrwxs77] | Link zum Applet (falls es nicht vollständig dargestellt wird):[https://www.geogebra.org/m/xqrwxs77] br> | ||
<ggb_applet id=" | <ggb_applet id="pds2u3jn" width="519" height="659" border="888888" /> | ||
Applet von | Applet von Luc Morth<br> | ||
Link zum Applet (falls es nicht vollständig dargestellt wird):[https://www.geogebra.org/m/kAmAHEzU] | Link zum Applet (falls es nicht vollständig dargestellt wird):[https://www.geogebra.org/m/kAmAHEzU] | ||
<ggb_applet id=" | <ggb_applet id="UEdR9CNz" width="1890" height="839" border="888888" /> | ||
Applet von | Applet von G.von Lechberg<br> | ||
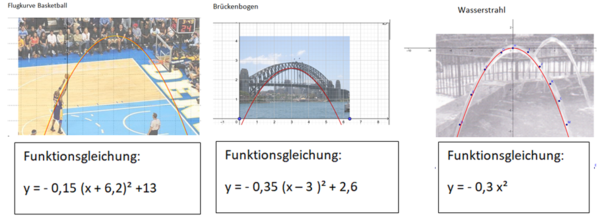
{{Lösung versteckt|[[Datei:Parabelbögen mit Funktionsgleichung (Einstieg GeoGebra).png|rahmenlos|600x600px]]|Vergleiche deine Lösung|Verbergen}} | {{Lösung versteckt|[[Datei:Parabelbögen mit Funktionsgleichung (Einstieg GeoGebra).png|rahmenlos|600x600px]]|Vergleiche deine Lösung|Verbergen}} | ||
Version vom 28. Juni 2021, 13:27 Uhr
SEITE IM AUFGBAU
Mögliche Fragen könnten sein:
- In welcher Höhe wird der Ball abgeworfen?
- Wie hoch fliegt der Ball maximal?
- Wie weit fliegt der Ball?
| Frage | Mathematik |
| In welcher Höhe wird der Ball abgeworfen? | Schnittpunkt mit der y-Achse, y-Achsenabschnitt
x = 0 |
| Wie hoch fliegt der Ball maximal? | Scheitelpunkt S (d|e) |
| Wie weit fliegt der Ball? | Nullstelle
y = 0 |
Die Flugkurven haben alle eine Gemeinsamkeit. Ihre Form nennt man Parabel. Sie sind die Graphen/Schaubilder quadratischer Funktionen.
(auch als kahoot!)
Link zum Applet (falls es nicht vollständig dargestellt wird): [1]

Applet von Bobby Knurek
Link zum Applet (falls es nicht vollständig dargestellt wird):[2] br>

Applet von Luc Morth
Link zum Applet (falls es nicht vollständig dargestellt wird):[3]

Applet von G.von Lechberg