Benutzer:Buss-Haskert/Quadratische Funktionen

SEITE IM AUFGBAU

Quadratische Funktionen und Gleichungen

In diesem Lernpfad zu quadratischen Funktionen und Gleichungen lernst du

...

Die Aufgaben beziehen sich auf das Buch "Schnittpunkt Mathematik - Differenzierende Ausgabe" des Klett-Verlages

Mathematik im Sportunterricht

Wähle eine Wurf-bzw. Stoßbewegung aus und beantworte die nachfolgenden Fragen.

• Weitwurf
• Kugelstoßen
• Weitsprung
• Basketball-Korbwurf

Beobachte jeweils die Flugkurve des Balls/der Kugel/der springenden Person und skizziere diese im Heft.
Welche Bedeutung haben die Koordinatenachsen? Beschrifte!

Stelle Fragen, die mithilfe der gezeichneten Kurve beantwortet werden können.

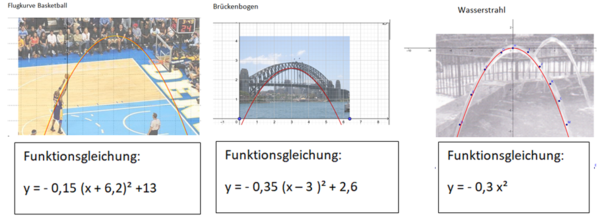
Mögliche Fragen könnten sein:

• In welcher Höhe wird der Ball abgeworfen?
• Wie hoch fliegt der Ball maximal?
• Wie weit fliegt der Ball?

Frage	Mathematik
In welcher Höhe wird der Ball abgeworfen?	Schnittpunkt mit der y-Achse, y-Achsenabschnitt x = 0
Wie hoch fliegt der Ball maximal?	Scheitelpunkt S (d|e)
Wie weit fliegt der Ball?	Nullstelle y = 0

Die Flugkurven haben alle eine Gemeinsamkeit. Ihre Form nennt man Parabel und sie können als quadratische Funktionen dargestellt werden.

Übung 1 (HA)

Suche parabelförmige Bögen in deiner Umgebung. Fotografiere mindestens eine Parabel, notiere, wo du sie entdeckt hast und wie sie aussieht (z.B. breit, schmal, nach oben oder nach unten geöffnet). Lade das Foto im Gruppenordner Mathematik hoch.

Übung 2 Parabel und Gleichung

• Skizziere die Flugkuren/Bögen aus den Applets in dein Heft.
• Notiere die passende Funktionsgleichung.
• Notiere Gemeinsamkeiten und Unterschiede der Flugkurven und Funktionsgleichungen.

Link zum Applet (falls es nicht vollständig dargestellt wird): [1]

Applet von Bobby Knurek

Link zum Applet (falls es nicht vollständig dargestellt wird):[2] [3]

Applet von Andreas Fischer

Link zum Applet (falls es nicht vollständig dargestellt wird):[4] [5]

Applet von L.Böker