Benutzer:ClaraS WWU-7/Testseite: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 80: | Zeile 80: | ||
4. Die Kugel ist blau. | 4. Die Kugel ist blau. | ||
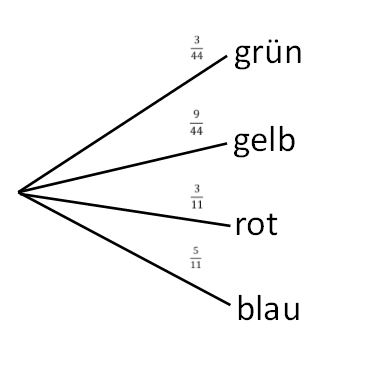
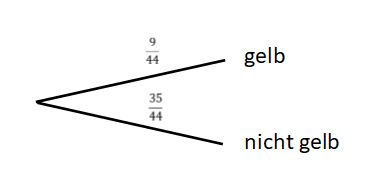
Die Wahrscheinlichkeit errechnet sich dann aus der absoluten Häufigkeit der Kugeln. | Die Wahrscheinlichkeit errechnet sich dann aus der absoluten Häufigkeit der Kugeln. Das Baumdiagramm sieht dann so aus: | ||
[[Datei:Baumdiagramm A2 a.jpg|zentriert]] | [[Datei:Baumdiagramm A2 a.jpg|zentriert]] | ||
| Zeile 90: | Zeile 90: | ||
2. Die Kugel ist nicht gelb. | 2. Die Kugel ist nicht gelb. | ||
Die Wahrscheinlichkeit dafür, dass die Kugel gelb ist, ergibt sich dann aus der absoluten Häufigkeit der gelben Kugeln. Die Wahrscheinlichkeit dafür, dass die Kugel nicht gelb ist | Die Wahrscheinlichkeit dafür, dass die Kugel gelb ist, ergibt sich dann aus der absoluten Häufigkeit der gelben Kugeln. Die Wahrscheinlichkeit dafür, dass die Kugel nicht gelb ist efolgt aus der Komplementärregel. | ||
{{Box | Komplementärregel| | {{Box | Komplementärregel| | ||
Hat ein Experiment genau zwei EReignisse, so spricht man von Ereignis und Gegenereignis. Die Wahrscheinlichkeiten der beiden ergeben in der Summe 1 | Hat ein Experiment genau zwei EReignisse, so spricht man von Ereignis und Gegenereignis. Die Wahrscheinlichkeiten der beiden ergeben in der Summe 1: | ||
<math>P(E)+P(\bar E)=1</math> | <math>P(E)+P(\bar E)=1</math> | ||
| Zeile 99: | Zeile 99: | ||
| Merksatz}} | | Merksatz}} | ||
Das Baumdiagramm sieht dann so aus: | |||
[[Datei:Baumdiagramm A2 a alternativ.jpg|zentriert]] | |||
Rechne das nun in Prozent um: | |||
<math>\tfrac{9}{44} \approx 0,2045 = 20,45 %.</math> | |||
|2= Lösung |3= Lösung }} | |||
Die Wahrscheinlichkeit einen Stift zu gewinnen liegt bei 20,45%. | Die Wahrscheinlichkeit einen Stift zu gewinnen liegt bei 20,45%. | ||
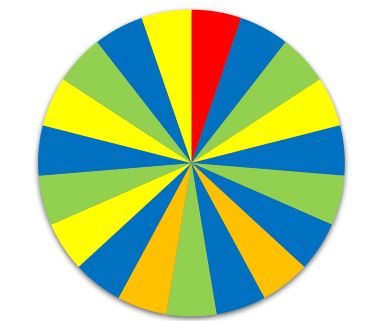
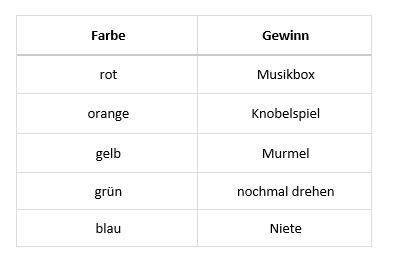
'''b)''' Oben auf dem Plakat steht: "Hier ist Gewinnen wahrscheinlicher, als Verlieren!". Stimmt das? Berechne zunächst die einzelnen Wahrscheinlichkeiten. Gibt die Lösung wieder in Prozent an. | '''b)''' Oben auf dem Plakat steht: "Hier ist Gewinnen wahrscheinlicher, als Verlieren!". Stimmt das? Berechne zunächst die einzelnen Wahrscheinlichkeiten. Gibt die Lösung wieder in Prozent an. | ||
Version vom 20. November 2020, 17:53 Uhr
Zufallsversuche
Für die nächsten Aufgaben benötigst du Stift, Papier und Taschenrechner. Bitte runde Dezimalzahlen auf 2 Nachkommastellen.