Benutzer:ClaraS WWU-7/Testseite: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Zeile 1: Zeile 1:
==== Zufallsversuche ====
====Zufallsversuche====


Die nächsten Aufgaben solltest du mit Stift, Papier und Taschenrechner lösen.
Für die nächsten Aufgaben benötigst du Stift, Papier und Taschenrechner. Du wirst hier und da Infoboxen finden, in denen verschiedene Begriffe oder Verfahren erklärt sind. Außerdem werden einige Beispiel angegeben. Sowohl die Infoboxen als auch die Beispiele sind mit dem Hinweis: "Information" verlinkt.  


{{Box | Wahrscheinlichkeiten berechnen| Zunächst zählst du, wie viele '''Ergebnisse''' es gibt. Die Ergebnisse sind alle möglichen Fälle, die bei einem Zufallsexperiment eintreten können. Dann schaust du nach den '''Ereignissen'''. Wie viele der Ergebnisse treffen auf das Ereignis zu? Die Wahrscheinlichkeit berechnet sich aus <math>\tfrac{Anzahl der Ereignisse}{Anzahl der Ergebnisse}</math>. | Merksatz}}
{{Box | Wahrscheinlichkeiten berechnen| Zunächst zählst du, wie viele '''Ergebnisse''' es gibt. Die Ergebnisse sind alle möglichen Fälle, die bei einem Zufallsexperiment eintreten können. Dann schaust du nach den '''Ereignissen'''. Wie viele der Ergebnisse treffen auf das Ereignis zu? Die Wahrscheinlichkeit berechnet sich aus <math>\tfrac{Anzahl der Ereignisse}{Anzahl der Ergebnisse}</math>. | Merksatz}}
Zeile 61: Zeile 61:
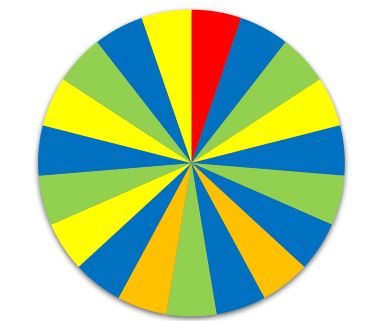
{{Box | Aufgabe 3: Münteraner Send |Auf dem Münsteraner Send gibt es ein Glücksrad. Es sieht wie folgt aus:
{{Box | Aufgabe 3: Münteraner Send |Auf dem Münsteraner Send gibt es ein Glücksrad. Es sieht wie folgt aus:


Glücksrad
[[Datei:Glücksrad A3.jpg|zentriert]]


Außerdem wird erklärt:  
Man kann Folgendes gewinnen:


Erklärung
{| class="wikitable"
!Farbe
!Gewinn
|-
|rot
|Musikbox
|-
|orange
|Gutschein für ein Fahrgeschäft deiner Wahl
|-
|gelb
|Knobelspiel
|-
|grün
|nochmal drehen
|-
|blau
|Niete
|}


'''a)''' Du hast einmal gedreht und landest auf einem grünen Feld. Du darfst also nochmal drehen. Du gewinnst den ersten Preis. Wie groß ist die Wahrscheinlichkeit, dass diese beiden Fälle direkt hintereinander eintreten?
'''a)''' Du hast einmal gedreht und landest auf einem grünen Feld. Du darfst also nochmal drehen. Beim zweiten Mal drehen landest du auf dem roten Feld. Wie groß ist die Wahrscheinlichkeit, dass diese beiden Fälle direkt hintereinander eintreten?


{{Lösung versteckt| 1= Wie groß ist die Wahrscheinlichkeit nochmal drehen zu dürfen? Zeichne hierzu ein Baumdiagramm {{Lösung versteckt| 1= Nun kannst du das Baumdiagramm fortführen. Erinnerst du dich an die Pfadregeln? {{Lösung versteckt|1= Erklärung Pfadregeln
{{Lösung versteckt| 1= Wie groß ist die Wahrscheinlichkeit nochmal drehen zu dürfen? Zeichne hierzu ein Baumdiagramm {{Lösung versteckt| 1= Nun kannst du das Baumdiagramm fortführen. Erinnerst du dich an die Pfadmultiplikationsregel? {{Lösung versteckt|1= {{Box | Pfadmultiplikationsregel| Die | Merksatz}}
  |2= Pfadregeln? Was war das nochmal genau? |3= Pfadregeln? Was war das nochmal genau?}}
 
  |2=Inormation|3= Information}}
|2=Tipp|3= Tipp}}|2=Tipp|3=Tipp}}  
|2=Tipp|3= Tipp}}|2=Tipp|3=Tipp}}  


Version vom 18. November 2020, 13:07 Uhr

Zufallsversuche

Für die nächsten Aufgaben benötigst du Stift, Papier und Taschenrechner. Du wirst hier und da Infoboxen finden, in denen verschiedene Begriffe oder Verfahren erklärt sind. Außerdem werden einige Beispiel angegeben. Sowohl die Infoboxen als auch die Beispiele sind mit dem Hinweis: "Information" verlinkt.


Wahrscheinlichkeiten berechnen
Zunächst zählst du, wie viele Ergebnisse es gibt. Die Ergebnisse sind alle möglichen Fälle, die bei einem Zufallsexperiment eintreten können. Dann schaust du nach den Ereignissen. Wie viele der Ergebnisse treffen auf das Ereignis zu? Die Wahrscheinlichkeit berechnet sich aus .


Beispiel
Münzwurf. Die Ergebnisse sind Kopf und Zahl. Es gibt also 2 Ergebnisse. Nun Möchtest du wissen, mit welcher Wahrscheinlichkeit du Kopf erhälst. Kopf ist ein Ereignis. Die Warscnienlichkeit ist


Aufgabe 1: Klassendienste

In einer Klasse sind 14 Jungen und 13 Mädchen. Es werden Beauftragte für verschiedene Klassendienste gelost.

a)Für den Blumendienst wird eine Person gelost. Wie groß ist die Wahrscheinlichkeit, dass es ein Junge ist?

Zeichne ein Baumdiagramm. Wie viele Ausgänge gibt es?
Die Wahrscheinlichkeit, dass ein Junge den Dienst bekommt, liegt bei .

b) Für den Tafeldienst wird auch ein Zettel gezogen, jedoch hat die Lehrperson nun auch einen Zettel mit ihrem Namen hinzugefügt. Wie groß ist die Wahrscheinlichkeit, dass sie gezogen wird?

Wie viele Zettel sind nun in der Urne?
Zeichne ein Baumdiagramm. Wie viele Ausgänge gibt es?
Die Wahrscheinlichkeit dafür, dass die Lehrperson selbst die Tafel putzen muss, liegt bei .


Aufgabe 2: Schulfest

Bei eurem Schulfest gibt es eine Tombola. Bevor du blind ziehen darfst, wird dir einmal der Inhalt gezeigt, du zählst die Kugeln. Außerdem steht ein Schild neben der Urne (Abbildung 2). Du kannst auf dieBilder klicken, um sie in vergrößerter Form zu sehen.

Abbildung 1
Abbildung 2
Es sind 20 blaue Kugeln, 12 rote, 9 gelbe und 3 grüne.

Nun ziehst du blind eine Kugel.

a) Wie groß ist die Wahrscheinlichkeit, dass du einen Stift gewinnst (gelbe Kugel)? Gib die Lösung in Prozent an.

Zeichne ein Baumdiagramm. Wie viele Ausgänge gibt es?
Die Wahrscheinlichkeit einen Stift zu gewinnen liegt bei 20,45%.

b) Oben auf dem Plakat steht: "Hier ist Gewinnen wahrscheinlicher, als Verlieren!". Stimmt das? Berechne zunächst die einzelnen Wahrscheinlichkeiten. Gibt die Lösung wieder in Prozent an.

Zeichne ein Baumdiagramm. Wie viele Ausgänge gibt es?

Stimmt die Aussage auf dem Plakat?

ja
nein


Die Wahrscheinlichkeit, zu gewinnen liegt bei 54,55 %, die zu verlieren bei 45,45%.


Aufgabe 3: Münteraner Send

Auf dem Münsteraner Send gibt es ein Glücksrad. Es sieht wie folgt aus:

Glücksrad A3.jpg

Man kann Folgendes gewinnen:

{
Abgerufen von „https://projekte.zum.de/index.php?title=Benutzer:ClaraS_WWU-7/Testseite&oldid=35268“