Buss-Haskert/Quadratische Gleichungen

SEITE IM AUFBAU !!!

Lernpfad Quadratische Gleichungen

In diesem Lernpfad lernst du

• was quadratische Gleichungen sind,
• wie du quadratische Gleichungen lösen kannst,
• wie du Anwendungsaufgaben mithilfe von quadratischen Gleichungen löst.
  

Bearbeite die Schritte des Lernpfades selbständig. Stelle Fragen, wo du unsicher bist. Achte auf die Zeit!!

In der Fahrschule lernst du eine Faustformel für die Berechnung des Bremsweges:

Bremsweg in m:   s_B = ($\tfrac{v}{10}$)²

"s" bedeutet Weg bzw. Strecke; v steht für Geschwindigkeit (engl. velocity)

Hier handelt es sich um eine quadratische Gleichung, da die Variable v quadriert wird (v²).

Berechne den Bremsweg, wenn das Auto mit einer Geschwindigkeit von 30km/h fährt, also v=30 und wenn es mit einer Geschwindigkeit von 50km/h unterwegs ist.

Was fällt dir auf?
Vor Schulen oder Kindergärten sollten die Bremswege möglichst kurz sein. Wie schnell darf ein Auto fahren, damit der Bremsweg höchstens 4m beträgt?

Wenn v=30 beträgt, ist s_B = ($\tfrac{30}{10}$)² = 3² = 9 (m)
Für v=50 ist s_B = ($\tfrac{50}{10}$)² = 5² = 25(m)
Der Bremsweg ist also bei 50 km/h deutlich länger als bei 30 km/h, denn er hängt vom Quadrat der Geschwindigkeit ab.

Hier ist s=4m gegeben, die Gleichung muss also nach v aufgelöst werden. Dies lernst du in diesem Lernpfad!

Du siehst: Mathe ist überall! Du erarbeitest nun die Grundlagen zum Lösen solcher quadratischer Gleichungen.

1) Was sind quadratische Gleichungen?

Quadratische Gleichungen sind Gleichungen, in denen die Variable in zweiter Potenz (also z.B. x²) vorkommt.

Erinnerung: Lineare Gleichungen sind Gleichungen, in denen die Variable nur in erster Potenz (also z.B. x = x¹) vorkommt.

Entscheide in der nachfolgenden LearningApp, ob es sich um eine quadratische Gleichung handelt oder nicht.

2) Wie löse ich quadratische Gleichungen?

Quadratische Gleichungen kannst du zeichnerisch und rechnerisch lösen. Nutze für die zeichnerische Lösung GeoGebra und prüfe so immer deine rechnerischen Lösungen. Es gibt verschiedene Formen quadratischer Gleichungen. Die Lösungsstrategie hängt von der Form ab. Dies erklären die folgenden Kapitel.

2.1) Rein quadratische Gleichungen lösen

In der obigen Faustformel kommt die Variable v nur in quadratischer Form vor, also nur als v². Solche Gleichungen heißen "rein quadratisch". Sie haben immer die Form ax² = d (hier umgeformt $\tfrac{1}{100}$v² = s_B)

Rein quadratische Gleichungen

Eine quadratische Gleichung heißt rein quadratisch, wenn die Variable ausschließlich in der zweiten Potenz vorkommt:

    ax² = d

Diese Gleichungen zu lösen hast du schon in der 9. Klasse gelernt. Wiederhole dein Wissen mithilfe der nachfolgenden Aufgaben.

Übung 1

Löse Buch

• S. 32 Nr. 10
• S. 35 Nr. 18
• S. 35 Nr. 19
• S. 35 Nr. 20

Erinnerung: Gehe beim Lösen von Gleichungen immer "rückwärts" vor, also zuerst die Strichrechnung, dann die Punktrechnung, dann die Potenzen und Klammern.
Rechne hier also zuerst +100, dann :3 und zum Schluss ziehe die Wurzel.

Bringe zunächst alle Terme mit x² auf eine Seite der Gleichung und dann alle Terme ohne Variable auf die andere Seite. Teile durch den Koeffizienten von x² und ziehe dann die Wurzel:
15x² - 2 = 6x² - 1 | -6x²
9x² - 2 = -1 | +2
9x² = 1 |:9
x² = $\tfrac{1}{9}$ |$\surd$

x₁ = $\tfrac{1}{3}$ ; x₂ = -$\tfrac{1}{3}$

Beseitige zunächst die Brüche, indem du mit dem Nenner multiplizierst.
Beispiel a):
$\tfrac{x^2}{3}$ = 12 |∙3
x² = 36 |$\surd$

x₁ = 6 ; x₂ = -6

Übung 2

Löse die nachfolgende App.

Was ist die bei der letzten Aufgabe aufgefallen?

Bei der letzten Aufgabe muss im letzten Schritt $\sqrt{-2}$ berechnet werden. Dies ist nicht möglich, da das Quadrat einer Zahl niemals negativ ist, also die Wurzel nie aus einer negativen Zahl gezogen werden kann.

In den obigen Aufgaben erkennst du, dass eine rein quadratische Gleichung mehrere Lösungen haben kann:
zwei Lösungen, eine Lösung oder keine Lösung. Wovon hängt die Anzahl der Lösungen ab? Erkläre und begründe mithilfe der nachfolgenden Beispiele:

Zwei Lösungen:

1. x² = 169  |

...

Eine Lösung:

2. 2x² + 10 = 10  |

...

Keine Lösung:

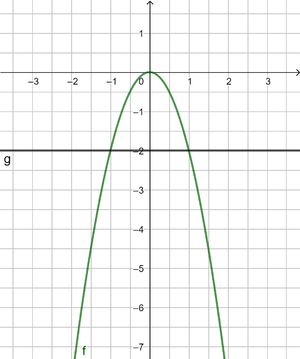
3. -3x² = 108  |

...

Anzahl der Lösungen quadratischer Gleichungen

Die Anzahl der Lösungen quadratischer Gleichungen hängt vom Radikand ab(vom Wert unter der Wurzel):

Die Gleichung hat zwei Lösungen, eine oder keine Lösung, wenn der Radikand positiv, null oder negativ ist.

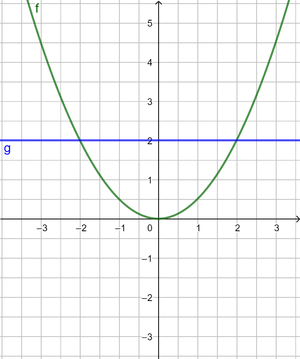
Du kannst diese Gleichungen auch grafisch lösen:
Beispiel:
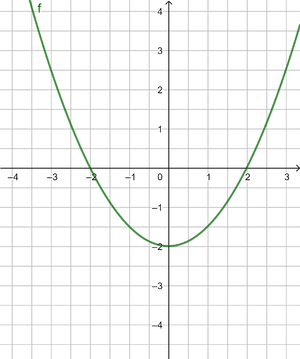
1. x² = 169 kannst du auch schreiben als x² - 169 = 0. Du berechnest also die Nullstellen der Funktion f(x) = x² - 169.

Übertrage die Zeichnung in dein Heft und erkläre die grafische Lösung.

Wie hilft dir das nachfolgende Applet bei der Lösung der Gleichung 0,5x² = 4,5 ? Erkläre im Heft!

Übung 3

Löse Buch

• S. 35 Nr. 22
• S. 35 Nr. 23
• S. 35 Nr. 24 a, b
  

Nutze zur Lösung bzw. zur Kontrolle die obigen Applets von GeoGebra.

Löse die Gleichung und schau auf den Wert unter der Wurzel: Ist es eine positive Zahl gibt es zwei Lösungen, ist der Wert unter der Wurzel 0, so gibt es genau eine Lösung und ist der Wert unter der Wurzel negativ, gibt es keine Lösung.

Nutze zur Lösung das obige Geogebra-Applet.

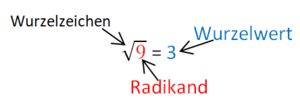
Löse die Gleichungen zunächst nach x auf. Die Variable a befindet sich dann immer unter dem Wurzelzeichen. Nun betrachte den Wert unter der Wurzel und prüfe, für welche Werte von a dieser positiv, null oder negativ ist.
Beispiel a):
x² - a = 0 |+a x² = a |$\surd$
Hier gibt es zwei Lösungen, wenn a eine positive Zahl ist, also a>0.

x₁ = $\sqrt{a}$; x₂ = -$\sqrt{a}$

Übung 4

Löse die Gleichungen ① $\dfrac{1}{2}$x² - 2 = 0 und ② -2x² + 2 = 0 zeichnerisch. Es gibt mehrere Möglichkeiten. Vergleiche deine Lösungen mit denen deines Partners.

1. Möglichkeit: Zeichne die Parabeln mithilfe einer Wertetabelle und lies die Nullstellen ab.
2. Möglichkeit: Forme die Gleichungen um in die Form ax² = d und zeichne die Parabel ax² und die Gerade y=d. Lies die Schnittpunkte ab.

1. Möglichkeit:

2. Möglichkeit:

2.2) Gemischt quadratische Gleichungen lösen

Eine Gleichung heißt "gemischt quadratisch", wenn die Variable in der zweiten Potenz (z.B. x²) und in einfacher Potenz (z.B. x) vorkommt.

2.2.1) Gleichungen der Form x² + bx = 0

Eine Gleichung heißt "gemischt quadratisch", wenn die Variable in der zweiten Potenz (z.B. x²) und in einfacher Potenz (z.B. x) vorkommt.
Beginnen wir mit dem besonderen Fall, dass die Gleichung die Form x² + bx = 0 hat, es also keinen Term "ohne" Variable gibt und eine Seite den Wert 0 hat.

Gemischt quadratische Gleichungen lösen durch Ausklammern

Hat die Gleichung die Form x² + bx = 0, so kannst du x ausklammern:
x² + bx = 0
x(x + b) = 0   Dieses Produkt wird nur 0, wenn einer der beiden Faktoren 0 ist (Satz vom Nullprodukt), also
x = 0 oder x + b = 0 |-b

x₁ = 0 oder x₂ = -b.

Übung 5

Löse die nachfolgende App, indem du zunächst die Gleichung durch Ausklammern in die Produktform umwandelst.

Übung 6

Löse Buch

• S. 28 Nr. 14
• S. 28 Nr. 15

Bringe die Gleichung zunächst in die Form x² + bx = 0 und löse dann wie in der LearningApp.

c) x² = 3x |-3x
x² - 3x = 0

Klammere nun x aus (wie in Übung 4)

2x² + 5x = 0 |Klammere 2x aus.
2x(x + 2,5) = 0 |Nullprodukt
2x = 0 oder x + 2,5 = 0

Den letzten Schritt schaffst du allein!

Bringe erst alle Terme auf die linke Seite, damit die rechte Seite den Wert 0 hat. Löse dann wie in 14d

Hier ist die Produktform schon gegeben. Es gilt wieder, dass ein Produkt nur 0 sein kann, wenn einer der Faktoren 0 ist:
(x + 4)(x + 5) = 0
x + 4 = 0 oder x + 5 = 0

x₁ = -4 oder x₂=-5.

2.2.2) Gleichungen der Form x² + bx + c = 0

Kannst du die folgenden Gleichungen lösen? Probiere aus und vergleiche deine Ideen mit denen deines Partners. 1. (x + 3)² = 0

2. x² + 6x + 9 = 0

3. x² -10x + 25 = 0

4. x² +4x - 5 = 0

Ziehe auf beiden Seiten die Wurzel, dann gilt x+3 = 0, also x = -3.
Hier hilft wieder die zeichnerische Lösung: Bestimme die Nullstellen der Funktion f(x)=(x+3)².

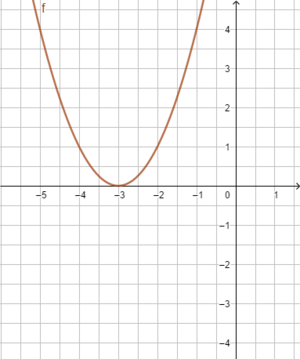
Hier siehst du auch, warum die Gleichung nur eine Lösung hat.

Kommt in der Gleichung neben x² und x auch noch ein Term ohne x vor, löst du die Gleichung mithilfe der quadratischen Ergänzung.

Gemischt quadratische Gleichungen lösen durch quadratische Ergänzung

Hat die Gleichung die Form x² + bx + c = 0, löst du die Gleichung mithilfe der quadratischen Ergänzung:

Stelle die Gleichung um: x² + bx = -c.
Mithilfe der quadratischen Ergänzung $\left ( \frac{b}{2} \right )^2$ auf beiden Seiten der Gleichung, wird dann der Term x² + bx zu einem Binom umgeformt. Dann wird auf beiden Seiten der Gleichung die Wurzel gezogen.