Herta-Lebenstein-Realschule/Die Scheitelpunktform quadratischer Funktionen sportlich erarbeiten: Unterschied zwischen den Versionen
K (GeoGebra Applet ausgetauscht) Markierung: 2017-Quelltext-Bearbeitung |
K (Lückentext ergänzt) Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 83: | Zeile 83: | ||
Detlef ist ebenfalls sportlich, allerdings auch ein wenig '''<big><big><big>d</big></big></big>'''usselig. Er läuft beim Sprint immer in die entgegengesetzte Richtung. | Detlef ist ebenfalls sportlich, allerdings auch ein wenig '''<big><big><big>d</big></big></big>'''usselig. Er läuft beim Sprint immer in die entgegengesetzte Richtung. | ||
<div class="lueckentext-quiz"> | |||
Gib jeweils den Scheitelpunkt der verschobenen Normalparabel an. | |||
f(x) = (x + 1)² S('''-1()'''|'''0()''' | |||
g(x) = (x - 2)² S('''2()'''|'''0()''' | |||
</div> | |||
<br /> | <br /> | ||
<gallery>Jumping-151842 1280.png|Bild von OpenClipart-Vectors auf Pixabay | <gallery>Jumping-151842 1280.png|Bild von OpenClipart-Vectors auf Pixabay | ||
Version vom 17. Juni 2020, 18:17 Uhr
- Anton: f(x) = ax²
Anton ist sehr sportlich, er spielt Basketball:
Öffne die Seite und verändere a mit dem Schieberegler.

Welche Auswirkungen hat der anton auf das Schaubild der Normalparabel?
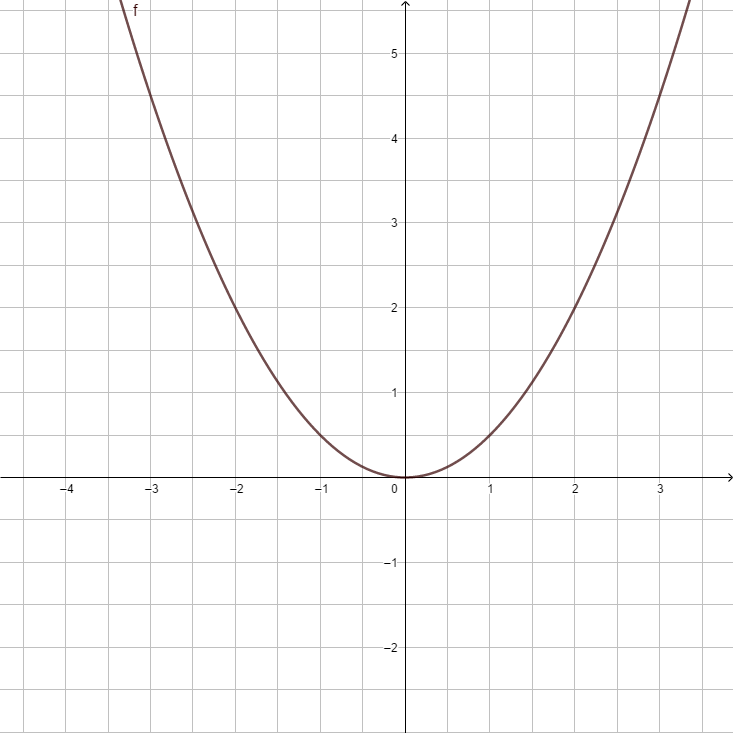
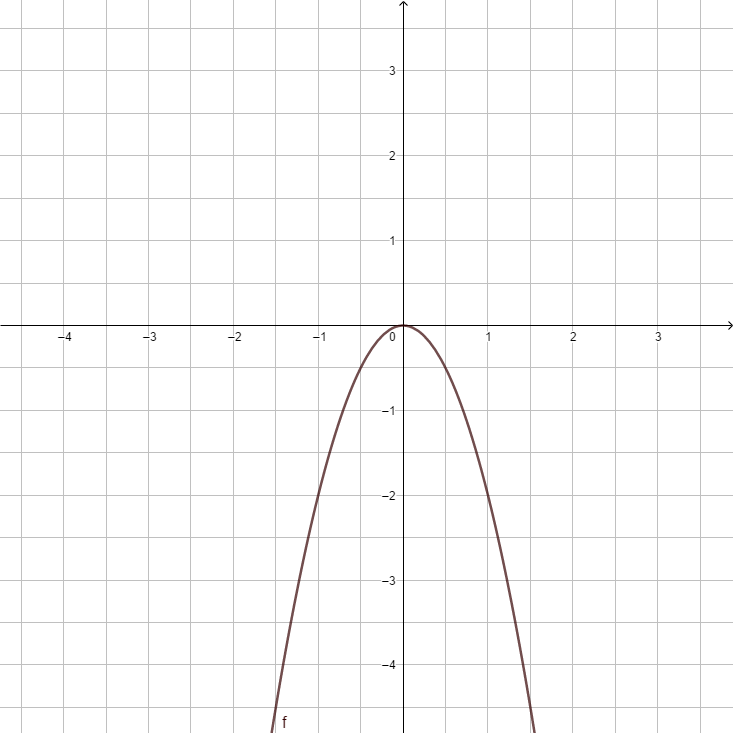
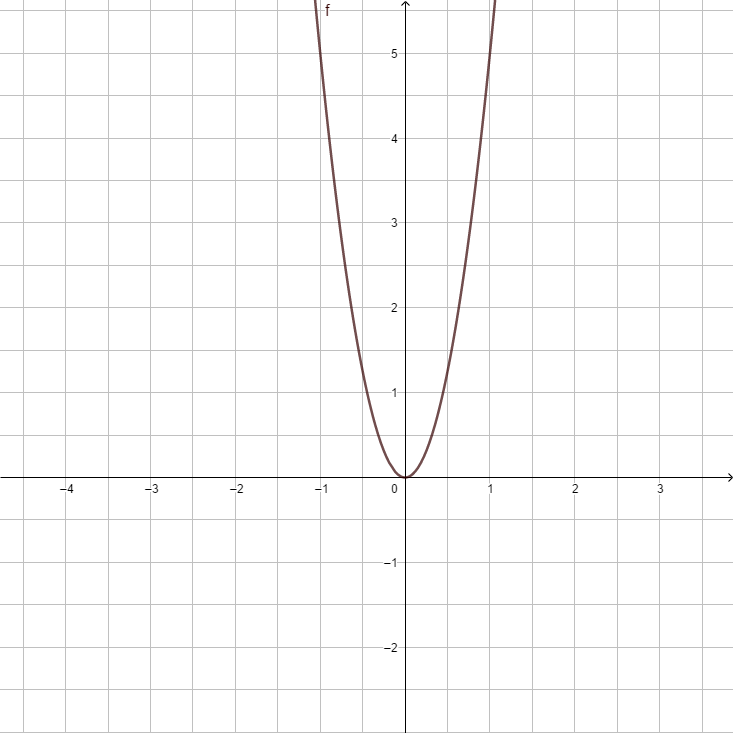
1. Beschreibe den Verlauf der Parabel f(x) = 5x2
(nach oben geöffnet) (!nach unten geöffnet) (gestreckt) (!gestaucht)
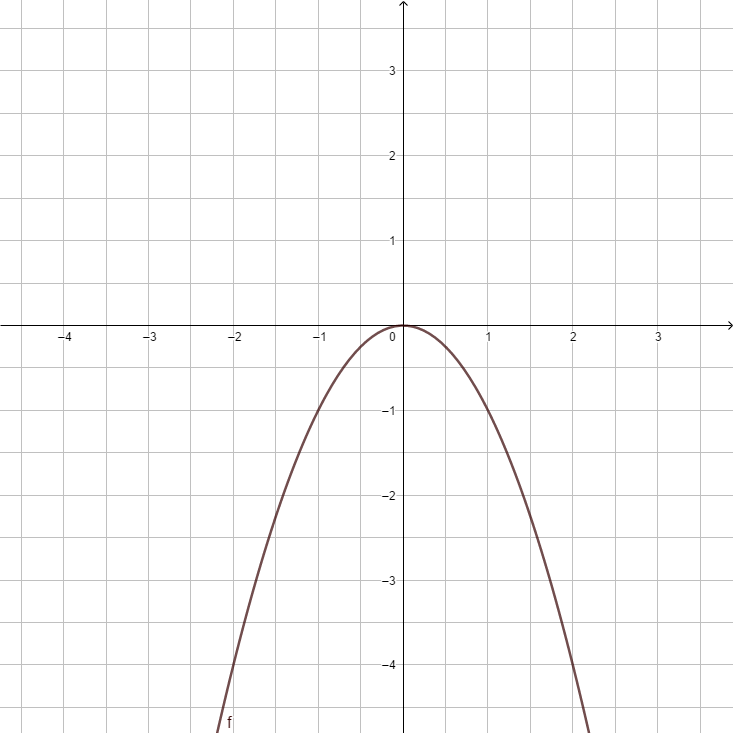
2. Beschreibe den Verlauf der Parabel f(x) = -3x2
(!nach oben geöffnet) (nach unten geöffnet) (gestreckt) (!gestaucht)
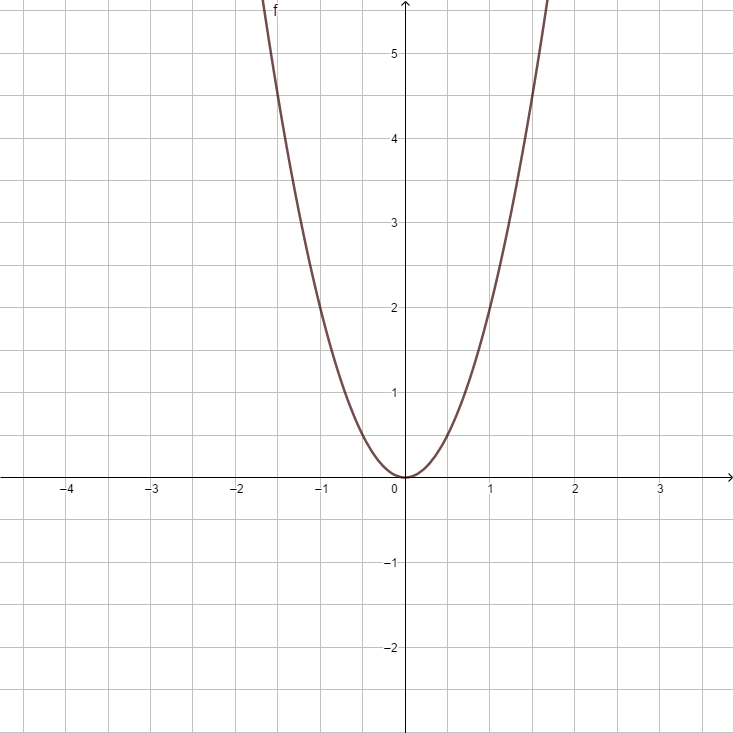
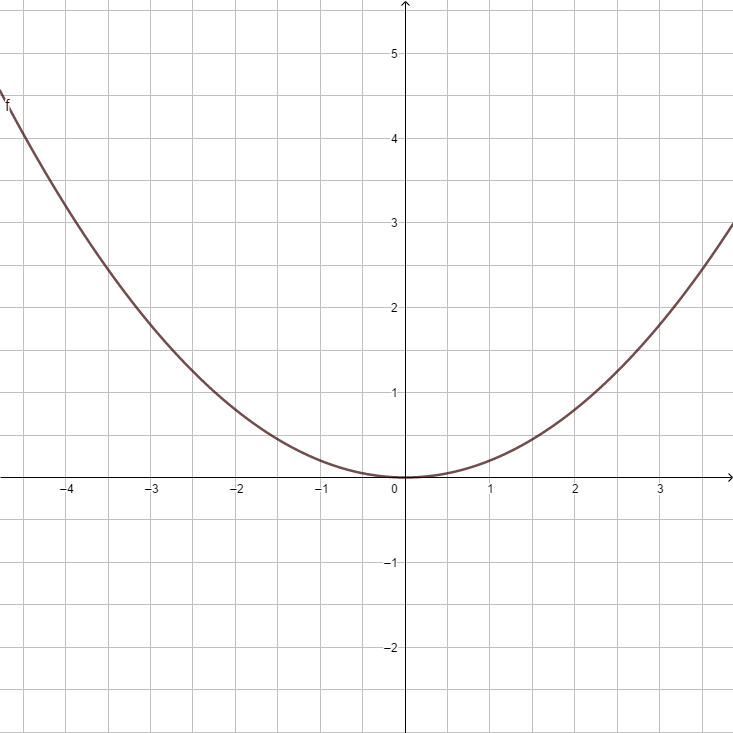
3. Beschreibe den Verlauf der Parabel f(x) = 0,5x2
(nach oben geöffnet) (!nach unten geöffnet) (!gestreckt) (gestaucht)
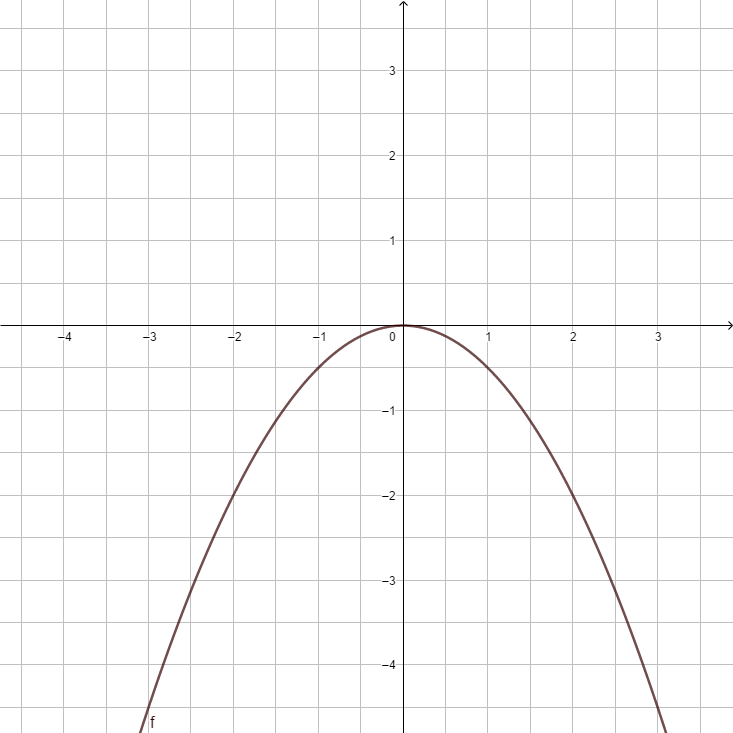
4. Beschreibe den Verlauf der Parabel f(x) = -x2
(!nach oben geöffnet) (nach unten geöffnet) (!gestreckt) (gestaucht)
2. Detlef: f(x) = (x + d)²
Detlef ist ebenfalls sportlich, allerdings auch ein wenig dusselig. Er läuft beim Sprint immer in die entgegengesetzte Richtung.
Gib jeweils den Scheitelpunkt der verschobenen Normalparabel an. f(x) = (x + 1)² S(-1()|0() g(x) = (x - 2)² S(2()|0()
Öffne die Seite und verändere d mit dem Schieberegler.

Welche Auswirkungen hat detlf auf das Schaubild der Normalparabel?
3. Emil: f(x) = x² + e
emil ist ebenfalls sehr sportlich:
Er kann sehr hoch springen, ebenso gut kann er tauchen.

Öffne die Seite und verändere e mit dem Schieberegler.

Welche Auswirkungen hat emil auf das Schaubild der Normalparabel?