Informatik am Johanneum/eigene Verfahren/12jojo

Spiralverfahren

Das “Spiralverfahren” ist ein monoalphabetisches Substitutionsverfahren. Der Name leitet sich hierbei von der Spirale ab, auf der das gesamte Verschlüsselungsverfahren basiert.

Für dieses Verschlüsselungsverfahren benutzt man einen Schlüssel, dieser besteht aus einem Wort/Buchstaben und einer Zahl. Das Wort kann hierbei auch nur ein einziger Buchstabe sein (Außnahme ist das A, mit nur diesem Buchstaben funktioniert das Verfahren nicht!), der Länge sind nach hinten keine Grenzen gesetzt. Die Zahl muss gerade sein und zwischen 4 und 24 liegen, bei einer ungeraden Zahl funktioniert das Verfahren nicht fehlerfrei. Diese Zahl gibt an in wie viele Teile die Spirale, die immer als Grundlage dient, geteilt werden muss.

Verschlüsselung

Um eine Nachricht zu verschlüsseln überlegt man sich also einen Schlüssel, der die Bedingungen erfüllt. Anschließend zeichnet man eine Spirale (ob gegen oder mit dem Uhrzeigersinn ist hierbei egal, Hauptsache man schreibt in die gleiche Richtung, in die man auch gezeichnet hat) und teilt diese in so viele Teile, wie im Schlüssel angegeben. Jetzt beginnt man im Zentrum der Spirale und schriebt jeweils einen Buchstaben in einen Teil, und wandert so immer weiter nach außen. Anfangen tut man mit dem Schlüsselwort, dieses steht also im Zentrum der Spirale. Enthält das Schlüsselwort Buchstaben mehrfach, streicht man die wiederholten Buchstaben (z.B.: Schlüsselwort: Schachtel -> Schatel (das c und das h fallen weg, da diese schon einmal in dem Wort vorkamen)). Nach dem Schlüsselwort schreibt man das Alphabet von vorne bis hinten weiter auf, dabei werden die im Schlüsselwort bereits enthaltenen Buchstaben übersprungen. Ist man mit dem Alphabet vollständig durch, fängt man noch einmal mit dem Schlüsselwort an und setzt es wie zuvor mit dem Alphabet fort, bis außen in der Spate des letzten Buchstabens des “ersten” Durchgangs noch zwei weitere Buchstaben in den Zeilen außerhalb sind. Jetzt muss anhand der gefüllten Spirale die Tabelle zum Ver- und Entschlüsseln mit Klartextalphabet und Geheimalphabet erstellt werden. Hierzu ersetzt man die Buchstaben nach einander abwechselnd mit dem Buchstaben einer oder zwei Stufen weiter außen. Der erste Buchstabe im Zentrum der Spirale wird durch den zweiten Buchstaben eine Stufe weiter außen in dem gleichen Teil der Spirale verschlüsselt, der zweite durch den zwei Stufen weiter außen liegenden Buchstaben im gleichen Teil, der dritte wieder durch den eine Stufe weiter außen liegenden Buchstaben usw. So verschlüsselt man alle Buchstaben wie durch eine Art Zick-Zack-Muster, das sich von innen nach außen durch die Spirale zieht.

Entschlüsselung

Entschlüsseln funktioniert ebenfalls durch die mit dem selber Verfahren erstellte Übersetzungstabelle.

Der Schlüssel muss hierfür natürlich bekannt sein, oder mit der verschlüsselten oder einer weiteren Nachricht übermittelt werden, damit der Empfänger die dazu passende Spirale zeichnen und die Tabelle zum ermitteln des Klartextes erstellen kann.

Beispiel

.

Verschlüsselung

Der Satz EINVERSCHLUESSLUNGSVERFAHRENSOLLTEAUCHEINFACHANZUWENDENSEIN lässt sich mit meinem Verfahren folgendermaßen verschlüsseln:

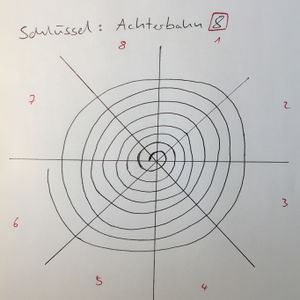
Der Schlüssel lautet "Achterbahn 8".

Man teilt also zunäcsht die Spirale in acht Spaten und beginnt anschließend damit das

Entschlüsselung

Schreibe hier, wie sich der verschlüsselte Satz wieder entschlüsseln lässt.

Sicherheitsbewertung

Die hohe Anzahl an möglichen Schlüsseln, die auch durch die Kombination von Buchstaben/Wörtern und Zahlen entsteht, macht das Verschlüsselungsverfahren grundsätzlich relativ sicher, leider ist das verfahren jedoch mit der Häufigkeitsanalyse der Buchstaben angreifbar. Damit lassen sich vor allem lange Texte vergleichsweise einfach und schnell auch ohne bekannten Schlüssel entschlüsseln.