Im Januar befällt ein neuartiges Virus Deutschland. Mittlerweile ist es Oktober und du suchst im Internet nach Informationen über die Infektionszahlen. Dort triffst du auf folgende Informationen:
- Im Dezember des Vorjahres befinden sich noch keine infizierten Personen in Deutschland
- Im April leben 2.000.000 infizierte Personen in Deutschland
- Im August leben 4.000.000 infizierte Personen in Deutschland
- Durch entsprechende Maßnahmen ist die Zahl infizierter Personen ab August rückläufig
a)
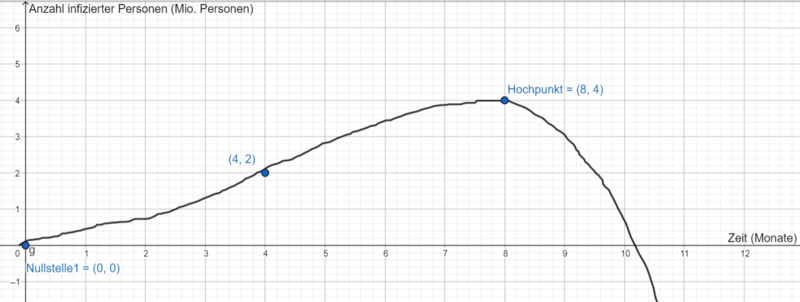
Stelle alle relevanten Informationen in einem geeigneten Koordinatensystem graphisch dar und skizziere einen möglichen Graphen. Beachte hierbei die geeignete Wahl der Einheiten.
Kann man den Monaten Zahlen zuweisen, um sie entlang einer Achse anzuordnen? Welche Einheit ist für die Anzahl infizierter Personen geeignet?
Der Graph hat bei entsprechender Wahl der Einheiten eine
Nullstelle bei 
, er verläuft durch den Punkt

und hat den
Hochpunkt 
Unterer Graph ist nur eine Möglichkeit einer ungefähren Modellierung der Virusinfektion!
b)
Die Anzahl infizierter Personen lässt sich durch eine kubische Funktion der Form  beschreiben. Stelle die Gleichung von
beschreiben. Stelle die Gleichung von  auf.
auf.
Um die vier Unbekannten

,

,

und

eindeutig zu bestimmen, benötigst du
vier Bedingungen aus den Informationen. Nutze dafür Teilaufgabe a).

,

,

,


c)
Forscher gehen nun (im Oktober) davon aus, dass noch im selben Jahr alle jemals infizierten Personen in Deutschland geheilt sind und entsprechend keine Fälle mehr in Deutschland auftreten. Prüfe diese Vorhersage anhand der Informationen.
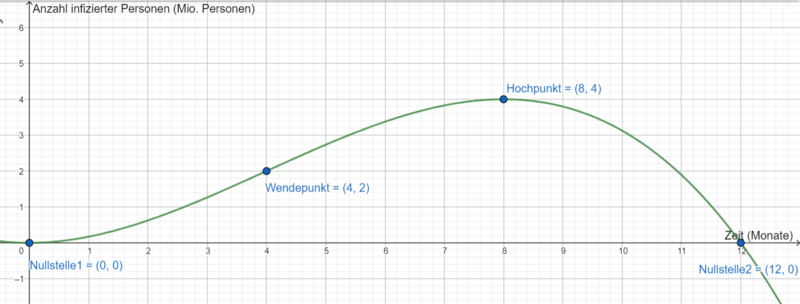
Zu den Zeitpunkten, zu denen keine infizierten Personen in Deutschland leben, hat der Graph seine Nullstellen.
Gleichungen, die nur Summanden mit der Variable

enthalten, lassen sich durch
Faktorisieren lösen .
d)
Forscher behaupten weiterhin, dass die milden Temperaturen im Frühling dafür sorgen, dass sich der temperaturempfindliche Virus optimal ausbreiten kann und deshalb die stärkste Zunahme infizierter Personen im Frühling nachzuweisen ist. Prüfe diese Behauptung anhand der Informationen.
Der Wendepunkt ist der Punkt der stärksten Zunahme (oder stärksten Abnahme) des Funktionsgraphen, der an dieser Stelle sein Krümmungsverhalten ändert.

e)
Skizziere nun den Graphen von  anhand der Informationen und vergleiche ihn mit dem Graphen aus Teilaufgabe a). Für welchen Zeitraum ist dieser Graph als mathematische Modellierung der Virusinfektion geeignet?
anhand der Informationen und vergleiche ihn mit dem Graphen aus Teilaufgabe a). Für welchen Zeitraum ist dieser Graph als mathematische Modellierung der Virusinfektion geeignet?
Da die Funktionswerte von

für

negativ sind, ist der Graph nur für

als mathematische Modellierung der Virusinfektion geeignet.