|
|
| Zeile 31: |
Zeile 31: |
|
| |
|
| =Test für unseren Lernpfad= | | =Test für unseren Lernpfad= |
| ===Den Schnittpunkt zweier Geraden bestimmen===
| |
|
| |
|
| {{Box|Das Steigungsdreieck| | | {{Box|Das Steigungsdreieck| |
| Zeile 41: |
Zeile 40: |
| <ggb_applet id="jbd6xgfh" width="750" height="500" border="888888" /> | | <ggb_applet id="jbd6xgfh" width="750" height="500" border="888888" /> |
| |Merke}} | | |Merke}} |
| | |
| | ===Lineare Funktionen - Bestimmung von Geradengleichungen=== |
|
| |
|
| {{Box|1=Aufgabe 4: Eine Geradengleichung mithilfe von zwei Punkten bestimmen|2= Gegeben seien stets zwei Punkte, durch die eine Gerade verläuft. Bestimme in deinem Heft die jeweiligen Gleichungen der Geraden in der Form <math>f(x) = mx + n</math>. | | {{Box|1=Aufgabe 4: Eine Geradengleichung mithilfe von zwei Punkten bestimmen|2= Gegeben seien stets zwei Punkte, durch die eine Gerade verläuft. Bestimme in deinem Heft die jeweiligen Gleichungen der Geraden in der Form <math>f(x) = mx + n</math>. |
| Zeile 147: |
Zeile 148: |
| |2 = Lösung|3 = Lösung}} | | |2 = Lösung|3 = Lösung}} |
|
| |
|
| | |3=Arbeitsmethode}} |
| | |
| | ===Prüfen, ob Punkte auf einer Geraden liegen=== |
| | {{Box |1=Aufgabe 5: Punkte auf dem Graphen|2=Prüfe für die angegebenen linearen Funktionen, welche Punkte auf dem Funktionsgraphen liegen. Arbeite zunächst im Heft und ordne dann jeder Funktion die Punkte zu, die auf ihrem Graphen liegen. Klicke dabei immer zunächst auf die Funktion und anschließend auf die zugehörigen Punkte. Im Hintergrund Hinweis: Einer Funktion können mehrere Punkte zugeordnet sein, aber jedem Punkt ist nur genau eine Funktion zugeordnet. |
| | |
| | {{LearningApp|width:100%|height:700px|app=p446x08nn19}}{{Lösung versteckt|1 = Beginne mit Punkten, die du leichter zuordnen kannst.|2=Tipp 1|3=Tipp 1}} |
| | |
| | {{Lösung versteckt|1 = Überlege, wie du feststellen kannst, welchen Funktionswert die Funktionen an einer bestimmten Stelle x annehmen.|2=Tipp 2|3=Tipp 2}}{{Lösung versteckt|1 = Wir setzen beispielhaft den x-Wert des Punktes <math>(-1|1)</math> in die Funktion <math>f(x) = 2x + 3</math> ein und prüfen den Funktionswert. Dann ergibt sich: <math>f(-1) = 2 \cdot (-1) + 3 = -2 + 3 = 1</math>. Der Punkt liegt also auf dem Graphen der Funktion.<br />Nun setzen wir in dieselbe Funktion noch den x-Wert des Punktes <math>(2|10)</math> ein. Es ergibt sich: <math>f(2) = 2 \cdot 2 + 3 = 4 + 3 = 7</math>. Der Funktionswert an der Stelle 2 ist nicht 10, sondern 7. Der Punkt <math>(2|10)</math> liegt also nicht auf dem Graphen.<br /> Für die anderen Punkte und Funktionen geht man genauso vor und erhält:<br /> Auf dem Graphen der Funktion <math>f(x) = 2x + 3</math> liegen die Punkte: <math>(-1|1)</math>,<math>(0|3)</math>,<math>(2|7)</math>,<math>(1|5)</math>.<br />Auf dem Graphen der Funktion <math>f(x) = -x + 12</math> liegen die Punkte: <math>(2|10)</math>,<math>(12|0)</math>,<math>(\frac{7}{2}|\frac{17}{2})</math>,<math>(9|3)</math>.<br />Auf dem Graphen der Funktion <math>f(x) = -\frac{2}{3}x-\frac{5}{3}</math> liegen die Punkte: <math>(-1|-1)</math>,<math>(5|-5)</math>.<br />Auf dem Graphen der Funktion <math>f(x) = \frac{3}{8}</math> liegen die Punkte: <math>(4|\frac{3}{8})</math>,<math>(9|\frac{9}{24})</math>.<br />|2 = Lösung|3 = Lösung}} |
| |3=Arbeitsmethode}} | | |3=Arbeitsmethode}} |
Version vom 25. Oktober 2019, 17:38 Uhr
Spielwiese
Schreiben im Wiki
Neben normalem Text kann man auch kursiven oder fett gedruckten Text schreiben. Ebenso ist eine Kombination aus beidem möglich. Grüner Text ist etwas schwieriger und funktioniert über die Quelltextbearbeitung.
Vorlagen
Ganz einfach per Mausklick aktivierbar.
Aufgabe
beliebiger Inhalt
Merksatz
beliebiger Inhalt
Dateien

Dies ist das neue Logo der WWU Münser.
Interaktive Applets
Kombinationen
Merke
Bei linearen Funktionen der Form

gibt

den Y-Achsenabschnitt des Graphen an.
Test für unseren Lernpfad
Lineare Funktionen - Bestimmung von Geradengleichungen
Aufgabe 4: Eine Geradengleichung mithilfe von zwei Punkten bestimmen
Gegeben seien stets zwei Punkte, durch die eine Gerade verläuft. Bestimme in deinem Heft die jeweiligen Gleichungen der Geraden in der Form  .
.
- Berechne zunächst die Steigung
 , indem du wie im Merkkasten zum Steigungsdreieck vorgehst.
, indem du wie im Merkkasten zum Steigungsdreieck vorgehst.
- Berechne anschließend den y-Achsenabschnitt
 , indem du die Steigung und einen der beiden Punkte in die Geradengleichung der Form
, indem du die Steigung und einen der beiden Punkte in die Geradengleichung der Form  einsetzt.
einsetzt.
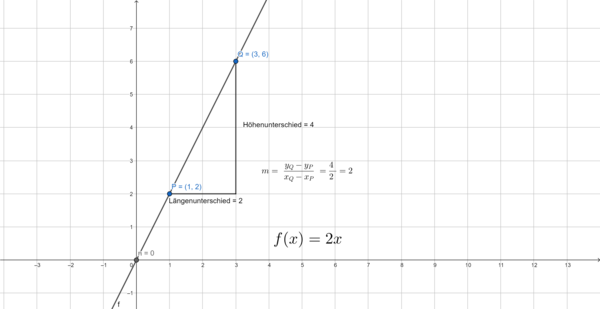
a) Gegeben seien die Punkte  und
und  .
.
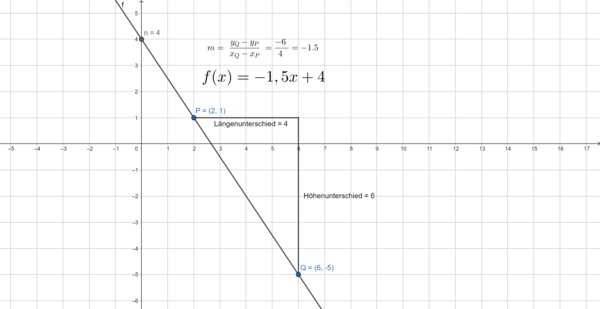
b) Gegeben seien die Punkte  und
und  .
.
Funktionsgleichung: 
- Für den Höhenunterschied der Punkte musst du die y-Koordinaten der Punkte
 und
und  wie folgt berechnen:
wie folgt berechnen:

- Für den Längenunterschied der Punkte musst du die x-Koordinaten der Punkte
 und
und  wie folgt berechnen:
wie folgt berechnen:

- Für die Steigung
 der Geraden musst du beide Werte in die folgende Gleichung einsetzen:
der Geraden musst du beide Werte in die folgende Gleichung einsetzen:

- Um den y-Achsenabschnitt zu berechen, setzt du die Steigung
 und einen der Punkte in die Geradengleichung
und einen der Punkte in die Geradengleichung  ein:
ein:
- Falls du als Punkt
 gewählt hast, erhälst du also
gewählt hast, erhälst du also 
- Falls du als Punkt
 gewählt hast, erhälst du also
gewählt hast, erhälst du also 
- Als letztes setzt du
 und
und  in die Geradengleichung
in die Geradengleichung  ein.
ein.
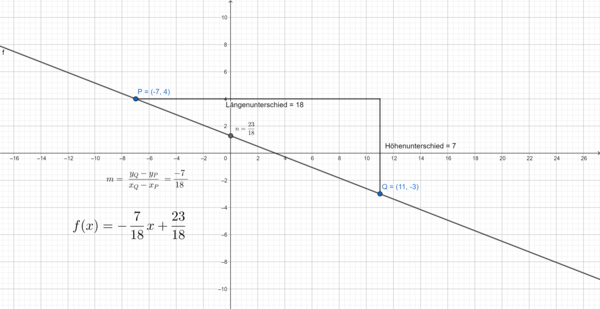
- Die beiden Gleichungen, die sich durch das Einsetzen der Punkte
 und
und  in die Geradengleichung
in die Geradengleichung  ergeben sind
ergeben sind  und
und  .
.
- Wenn du die beiden Gleichungen voneinander abziehst, kannst du
 eliminieren.
eliminieren.
- Nun kannst du eine Gleichung nach
 auflösen und erhälst
auflösen und erhälst  .
.
- Dies setzt du nun in die andere Gleichung für
 ein und erhälst
ein und erhälst  .
.
- Als letztes setzt du
 und
und  in die Geradengleichung
in die Geradengleichung  ein.
ein.
c) Gegeben seien die Punkte  und
und  .
.
Prüfen, ob Punkte auf einer Geraden liegen
Aufgabe 5: Punkte auf dem Graphen
Prüfe für die angegebenen linearen Funktionen, welche Punkte auf dem Funktionsgraphen liegen. Arbeite zunächst im Heft und ordne dann jeder Funktion die Punkte zu, die auf ihrem Graphen liegen. Klicke dabei immer zunächst auf die Funktion und anschließend auf die zugehörigen Punkte. Im Hintergrund Hinweis: Einer Funktion können mehrere Punkte zugeordnet sein, aber jedem Punkt ist nur genau eine Funktion zugeordnet.
Beginne mit Punkten, die du leichter zuordnen kannst.
Überlege, wie du feststellen kannst, welchen Funktionswert die Funktionen an einer bestimmten Stelle x annehmen.
Wir setzen beispielhaft den x-Wert des Punktes

in die Funktion

ein und prüfen den Funktionswert. Dann ergibt sich:

. Der Punkt liegt also auf dem Graphen der Funktion.
Nun setzen wir in dieselbe Funktion noch den x-Wert des Punktes

ein. Es ergibt sich:

. Der Funktionswert an der Stelle 2 ist nicht 10, sondern 7. Der Punkt

liegt also nicht auf dem Graphen.
Für die anderen Punkte und Funktionen geht man genauso vor und erhält:
Auf dem Graphen der Funktion

liegen die Punkte:

,

,

,

.
Auf dem Graphen der Funktion

liegen die Punkte:

,

,

,

.
Auf dem Graphen der Funktion

liegen die Punkte:

,

.
Auf dem Graphen der Funktion

liegen die Punkte:

,

.