Benutzer:Anja WWU-5/Testseite

Spielwiese

Schreiben im Wiki

Neben normalem Text kann man auch kursiven oder fett gedruckten Text schreiben. Ebenso ist eine Kombination aus beidem möglich. Grüner Text ist etwas schwieriger und funktioniert über die Quelltextbearbeitung.

Vorlagen

Ganz einfach per Mausklick aktivierbar.

Aufgabe

beliebiger Inhalt

Übung

beliebiger Inhalt

Merksatz

beliebiger Inhalt

Dateien

Dies ist das neue Logo der WWU Münser.

Kombinationen

Merke

Bei linearen Funktionen der Form $y=mx+n$ gibt $n$ den Y-Achsenabschnitt des Graphen an.

Arbeitsmethode

Bestimme die y-Achsenabschnitte folgender Funktionen:

(1) $y=2x+5$,          (2) $y=\frac{2}{3}x-1$      und     (3) $y=3$ ?

(1) $5$,          (2) $-1$      und     (3) $3$

Test für unseren Lernpfad

Den Schnittpunkt zweier Geraden bestimmen

Das Steigungsdreieck

Die Steigung einer linearen Funktion bestimmt man in der Regel mit folgenden Schritten:

1. Zunächst benötigt man zwei beliebige Punkte $P(x_P|y_P)$ und $Q(x_Q|y_Q)$.
2. Um den Höhenunterschied der Punkte zu bestimmen, benötigt man die y-Koordinaten der Punkte $P$ und $Q$.
   $H\ddot{o}henunterschied = y_Q - y_P$
3. Um den Längenunterschied der Punkte zu bestimmen, benötigt man die x-Koordinaten der Punkte $P$ und $Q$.
   $L\ddot{a}ngenunterschied = x_Q - x_P$
4. Für die Steigung $m$ der Geraden gilt:
   $m = \frac{H\ddot{o}henunterschied}{L\ddot{a}ngenunterschied} = \frac{y_Q - y_P}{x_Q - x_P}$

Aufgabe 4: Eine Geradengleichung mithilfe von zwei Punkten bestimmen

Gegeben seien stets zwei Punkte, durch die eine Gerade verläuft. Bestimme in deinem Heft die jeweiligen Gleichungen der Geraden in der Form $f(x) = mx + n$.

1. Berechne zunächst die Steigung $m$, indem du wie im Merkkasten zum Steigungsdreieck vorgehst.
2. Berechne anschließend den y-Achsenabschnitt $n$, indem du die Steigung und einen der beiden Punkte in die Geradengleichung der Form $f(x) = mx + n$ einsetzt.

Du kannst die Geradengleichung auch auf anderen Wegen erhalten:

• Lösung mit Hilfe eines linearen Gleichungssystems:
  • Stelle zwei Gleichungen mit jeweils den Unbekannten $m$ und $n$ auf, indem du die x-Koordinaten der Punkte $P$ und $Q$ für $x$ und die y-Koordinaten der Punkte $P$ und $Q$ für $f(x)$ in die Geradengleichung $f(x) = mx + n$ einsetzt.
  • Beide Gleichungen ergeben ein lineares Gleichungssystem, welches du zum Beispiel mit Hilfe des Eliminationsverfahres lösen kannst, um die beiden Unbekannten $m$ und $n$ zu bestimmen.
  • Die bestimmten Unbekannten setzt du anschließend in die Geradengleichung $f(x) = mx + n$ ein.
• Lösung mit Hilfe eines Graphen:
  • Zeichne die Punkte $P$ und $Q$ in ein Koordinatensystem ein.
  • Zeichne eine Gerade, die durch die Punkte $P$ und $Q$ verläuft.
  • Bestimme mit Hilfe des Steigungsdreiecks die Steigung $m$.
  • Lies den y-Achsenabschnitt $n$ am Graphen ab.
  • Setze alles in die Geradengleichung $f(x) = mx + n$ ein.

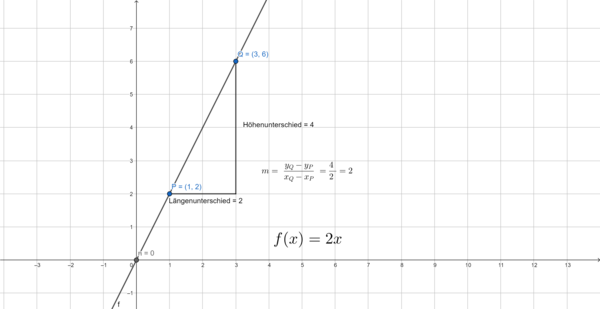
a) Gegeben seien die Punkte $P(1|2)$ und $Q(3|6)$.

Funktionsgleichung: $f(x) = 2x$

• Für den Höhenunterschied der Punkte musst du die y-Koordinaten der Punkte $P(1|2)$ und $Q(3|6)$ wie folgt berechnen:
  $H\ddot{o}henunterschied = y_Q - y_P = 6 - 2 = 4$
• Für den Längenunterschied der Punkte musst du die x-Koordinaten der Punkte $P(1|2)$ und $Q(3|6)$ wie folgt berechnen:
  $L\ddot{a}ngenunterschied = x_Q - x_P = 3 - 1 = 2$
• Für die Steigung $m$ der Geraden musst du beide Werte in die folgende Gleichung einsetzen:
  $m = \frac{H\ddot{o}henunterschied}{L\ddot{a}ngenunterschied} = \frac{y_Q - y_P}{x_Q - x_P} = \frac{4}{2} = \frac{2}{1} = 2$
• Um den y-Achsenabschnitt zu berechen, setzt du die Steigung $m = 2$ und einen der Punkte in die Geradengleichung $f(x) = mx + n$ ein:
  • Falls du als Punkt $P$ gewählt hast, erhälst du also $f(x) = mx + n \Leftrightarrow 2 = 2 \cdot 1 + n \Leftrightarrow 2 = 2 + n \Leftrightarrow 0 = n$
  • Falls du als Punkt $Q$ gewählt hast, erhälst du also $f(x) = mx + n \Leftrightarrow 6 = 2 \cdot 3 + n \Leftrightarrow 6 = 6 + n \Leftrightarrow 0 = n$
• Als letztes setzt du $m = 2$ und $n = 0$ in die Geradengleichung $f(x) = mx + n$ ein.

• Die beiden Gleichungen, die sich durch das Einsetzen der Punkte $P(1|2)$ und $Q(3|6)$ in die Geradengleichung $f(x) = mx + n$ ergeben sind $2 = m \cdot 1 + n$ und $6 = m \cdot 3 + n$.
• Wenn du die beiden Gleichungen voneinander abziehst, kannst du $n$ eliminieren.
• Nun kannst du eine Gleichung nach $m$ auflösen und erhälst $m = 2$.
• Dies setzt du nun in die andere Gleichung für $m$ ein und erhälst $n = 0$.
• Als letztes setzt du $m = 2$ und $n = 0$ in die Geradengleichung $f(x) = mx + n$ ein.

Graphischer Lösungsweg

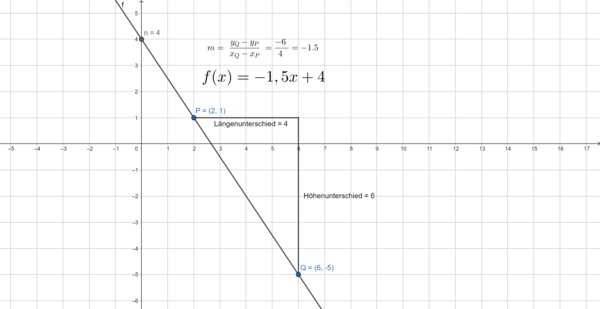
b) Gegeben seien die Punkte $P(2/1)$ und $Q(6/-5)$.

Funktionsgleichung: $f(x) = -1,5x + 4$

• Für den Höhenunterschied der Punkte musst du die y-Koordinaten der Punkte $P(2|1)$ und $Q(6|-5)$ wie folgt berechnen:
  $H\ddot{o}henunterschied = y_Q - y_P = -5 - 1 = -6$
• Für den Längenunterschied der Punkte musst du die x-Koordinaten der Punkte $P(2|1)$ und $Q(6|-5)$ wie folgt berechnen:
  $L\ddot{a}ngenunterschied = x_Q - x_P = 6 - 2 = 4$
• Für die Steigung $m$ der Geraden musst du beide Werte in die folgende Gleichung einsetzen:
  $m = \frac{H\ddot{o}henunterschied}{L\ddot{a}ngenunterschied} = \frac{y_Q - y_P}{x_Q - x_P} = \frac{-6}{4} = \frac{-3}{2} = -1,5$
• Um den y-Achsenabschnitt zu berechen, setzt du die Steigung $m = -1,5$ und einen der Punkte in die Geradengleichung $f(x) = mx + n$ ein:
  • Falls du als Punkt $P$ gewählt hast, erhälst du also $f(x) = mx + n \Leftrightarrow 1 = -1,5 \cdot 2 + n \Leftrightarrow 1 = -3 + n \Leftrightarrow 4 = n$
  • Falls du als Punkt $Q$ gewählt hast, erhälst du also $f(x) = mx + n \Leftrightarrow -5 = -1,5 \cdot 6 + n \Leftrightarrow -5 = -9 + n \Leftrightarrow 4 = n$
• Als letztes setzt du $m = -1,5$ und $n = 4$ in die Geradengleichung $f(x) = mx + n$ ein.

• Die beiden Gleichungen, die sich durch das Einsetzen der Punkte $P(2|1)$ und $Q(6|-5)$ in die Geradengleichung $f(x) = mx + n$ ergeben sind $1 = m \cdot 2 + n$ und $-5 = m \cdot 6 + n$.
• Wenn du die beiden Gleichungen voneinander abziehst, kannst du $n$ eliminieren.
• Nun kannst du eine Gleichung nach $m$ auflösen und erhälst $m = -1,5$.
• Dies setzt du nun in die andere Gleichung für $m$ ein und erhälst $n = 4$.
• Als letztes setzt du $m = -1,5$ und $n = 4$ in die Geradengleichung $f(x) = mx + n$ ein.

Graphischer Lösungsweg

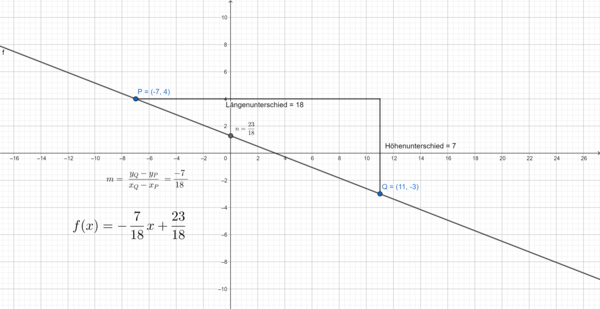
c) Gegeben seien die Punkte $P(-7/4)$ und $Q(11/-3)$.

Funktionsgleichung: $f(x) = -\frac{7}{18}x + \frac{23}{18}$

• Für den Höhenunterschied der Punkte musst du die y-Koordinaten der Punkte $P(-7|4)$ und $Q(11/-3)$ wie folgt berechnen:
  $H\ddot{o}henunterschied = y_Q - y_P = -3 - 4 = -7$
• Für den Längenunterschied der Punkte musst du die x-Koordinaten der Punkte $P(-7|4)$ und $Q(11/-3)$ wie folgt berechnen:
  $L\ddot{a}ngenunterschied = x_Q - x_P = 11 - (-7) = 11 + 7 = 18$
• Für die Steigung $m$ der Geraden musst du beide Werte in die folgende Gleichung einsetzen:
  $m = \frac{H\ddot{o}henunterschied}{L\ddot{a}ngenunterschied} = \frac{y_Q - y_P}{x_Q - x_P} = \frac{-7}{18} = -\frac{7}{18}$
• Um den y-Achsenabschnitt zu berechen, setzt du die Steigung $m = -\frac{7}{18}$ und einen der Punkte in die Geradengleichung $f(x) = mx + n$ ein:
  • Falls du als Punkt $P$ gewählt hast, erhälst du also $f(x) = mx + n \Leftrightarrow 4 = -\frac{7}{18} \cdot -7 + n \Leftrightarrow \frac{72}{18} = \frac{49}{18} + n \Leftrightarrow \frac{23}{18} = n$
  • Falls du als Punkt $Q$ gewählt hast, erhälst du also $f(x) = mx + n \Leftrightarrow -3 = -\frac{7}{18} \cdot 11 + n \Leftrightarrow -\frac{90}{18} = -\frac{77}{18} + n \Leftrightarrow \frac{23}{18} = n$
• Als letztes setzt du $m = -\frac{7}{18}$ und $n = \frac{23}{18}$ in die Geradengleichung $f(x) = mx + n$ ein.

• Die beiden Gleichungen, die sich durch das Einsetzen der Punkte $P(-7/4)$ und $Q(11/-3)$ in die Geradengleichung $f(x) = mx + n$ ergeben sind $4 = m \cdot -7 + n$ und $-3 = m \cdot 11 + n$.
• Wenn du die beiden Gleichungen voneinander abziehst, kannst du $n$ eliminieren.
• Nun kannst du eine Gleichung nach $m$ auflösen und erhälst $m = -\frac{7}{18}$.
• Dies setzt du nun in die andere Gleichung für $m$ ein und erhälst $n = \frac{23}{18}$.
• Als letztes setzt du $m = -\frac{7}{18}$ und $n = \frac{23}{18}$ in die Geradengleichung $f(x) = mx + n$ ein.

Graphischer Lösungsweg