Benutzer:Anja WWU-5/Testseite

Spielwiese

Schreiben im Wiki

Neben normalem Text kann man auch kursiven oder fett gedruckten Text schreiben. Ebenso ist eine Kombination aus beidem möglich. Grüner Text ist etwas schwieriger und funktioniert über die Quelltextbearbeitung.

Vorlagen

Versteckte Hinweise und Lösungen

Ganz einfach per Mausklick aktivierbar.

Aufgabe

beliebiger Inhalt

Übung

beliebiger Inhalt

Merksatz

beliebiger Inhalt

Dateien

Dies ist das neue Logo der WWU Münser.

Kombinationen

Merke

Bei linearen Funktionen der Form $y=mx+n$ gibt $n$ den Y-Achsenabschnitt des Graphen an.

Arbeitsmethode

Bestimme die y-Achsenabschnitte folgender Funktionen:

(1) $y=2x+5$,          (2) $y=\frac{2}{3}x-1$      und     (3) $y=3$ ?

Lösungsvorschläge anzeigen

(1) $5$,          (2) $-1$      und     (3) $3$

Test für unseren Lernpfad

Den Schnittpunkt zweier Geraden bestimmen

Das Steigungsdreieck

Die Steigung einer linearen Funktion bestimmt man in der Regel mit folgenden Schritten:

1. Zunächst benötigt man zwei beliebige Punkte $P(x_P|y_P)$ und $Q(x_Q|y_Q)$.
2. Um den Höhenunterschied der Punkte zu bestimmen, benötigt man die y-Koordinaten der Punkte $P$ und $Q$.
   $H\ddot{o}henunterschied = y_Q - y_P$
3. Um den Längenunterschied der Punkte zu bestimmen, benötigt man die x-Koordinaten der Punkte $P$ und $Q$.
   $L\ddot{a}ngenunterschied = x_Q - x_P$
4. Für die Steigung $m$ der Geraden gilt:
   $m = \frac{H\ddot{o}henunterschied}{L\ddot{a}ngenunterschied} = \frac{y_Q - y_P}{x_Q - x_P}$

Aufgabe 4: Eine Geradengleichung mithilfe von zwei Punkten bestimmen

Gegeben seien stets zwei Punkte, durch die eine Gerade verläuft. Bestimme in deinem Heft die jeweiligen Gleichungen der Geraden in der Form $f(x) = mx + n$.

Tipp: Allgemeines Vorgehen

1. Berechne zunächst die Steigung $m$, indem du wie im Merkkasten zum Steigungsdreieck vorgehst.
2. Berechne anschließend den y-Achsenabschnitt $n$, indem du die Steigung und einen der beiden Punkte in die Geradengleichung der Form $f(x) = mx + n$ einsetzt.

Tipp: Alternative Vorgehen

Du kannst die Geradengleichung auch auf anderen Wegen erhalten:

• Lösung mit Hilfe eines linearen Gleichungssystems:
  • Stelle zwei Gleichungen mit jeweils den Unbekannten $m$ und $n$ auf, indem du die x-Koordinaten der Punkte $P$ und $Q$ für $x$ und die y-Koordinaten der Punkte $P$ und $Q$ für $f(x)$ in die Geradengleichung $f(x) = mx + n$ einsetzt.
  • Beide Gleichungen ergeben ein lineares Gleichungssystem, welches du zum Beispiel mit Hilfe des Eliminationsverfahres lösen kannst, um die beiden Unbekannten $m$ und $n$ zu bestimmen.
  • Die bestimmten Unbekannten setzt du anschließend in die Geradengleichung $f(x) = mx + n$ ein.
• Lösung mit Hilfe eines Graphen:
  • Zeichne die Punkte $P$ und $Q$ in ein Koordinatensystem ein.
  • Zeichne eine Gerade, die durch die Punkte $P$ und $Q$ verläuft.
  • Bestimme mit Hilfe des Steigungsdreiecks die Steigung $m$.
  • Lies den y-Achsenabschnitt $n$ am Graphen ab.
  • Setze alles in die Geradengleichung $f(x) = mx + n$ ein.

a) Gegeben seien die Punkte $P(1|2)$ und $Q(3|6)$.

Lösung

Funktionsgleichung: $f(x) = 2x$

Tipp: Allgemeines Vorgehen

1. Berechne zunächst die Steigung $m$, indem du wie im Merkkasten zum Steigungsdreieck vorgehst.
2. Berechne anschließend den y-Achsenabschnitt $n$, indem du die Steigung und einen der beiden Punkte in die Geradengleichung der Form $f(x) = mx + n$ einsetzt.

Lösungsweg nach dem allgemeinen Verfahren:

• Für den Höhenunterschied der Punkte musst du die y-Koordinaten der Punkte $P(1|2)$ und $Q(3|6)$ wie folgt berechnen:
  $H\ddot{o}henunterschied = y_Q - y_P = 6 - 2 = 4$
• Für den Längenunterschied der Punkte musst du die x-Koordinaten der Punkte $P(1|2)$ und $Q(3|6)$ wie folgt berechnen:
  $L\ddot{a}ngenunterschied = x_Q - x_P = 3 - 1 = 2$
• Für die Steigung $m$ der Geraden musst du beide Werte in die folgende Gleichung einsetzen:
  $m = \frac{H\ddot{o}henunterschied}{L\ddot{a}ngenunterschied} = \frac{y_Q - y_P}{x_Q - x_P} = \frac{4}{2} = \frac{2}{1} = 2$
• Um den y-Achsenabschnitt zu berechen, setzt du die Steigung $m = 2$ und einen der Punkte in die Geradengleichung $f(x) = mx + n$ ein:
  • Falls du als Punkt $P$ gewählt hast, erhälst du also $f(x) = mx + n \Leftrightarrow 2 = 2 \cdot 1 + n \Leftrightarrow 2 = 2 + n \Leftrightarrow 0 = n$
  • Falls du als Punkt $Q$ gewählt hast, erhälst du also $f(x) = mx + n \Leftrightarrow 6 = 2 \cdot 3 + n \Leftrightarrow 6 = 6 + n \Leftrightarrow 0 = n$
• Als letztes setzt du $m = 2$ und $n = 0$ in die Geradengleichung $f(x) = mx + n$ ein.

Lösungsweg durch die Nutzung eines LGS:

• Die beiden Gleichungen, die sich durch das Einsetzen der Punkte $P(1|2)$ und $Q(3|6)$ in die Geradengleichung $f(x) = mx + n$ ergeben sind $2 = m \cdot 1 + n$ und $6 = m \cdot 3 + n$.
• Wenn du die beiden Gleichungen voneinander abziehst, kannst du $n$ eliminieren.
• Nun kannst du eine Gleichung nach $m$ auflösen und erhälst $m = 2$.
• Dies setzt du nun in die andere Gleichung für $m$ ein und erhälst $n = 0$.
• Als letztes setzt du $m = 2$ und $n = 0$ in die Geradengleichung $f(x) = mx + n$ ein.

Lösungsweg durch Nutzung eines Graphen:

Wenn du nach der ersten Variante vorgehen möchtest, also erst die Steigung $m$ und dann mithilfe eines der beiden Punkte $b$ bestimmen möchtest, dann ergibt sich zunächst für die Steigung: $m = \frac{f(x)_Q - f(x)_P}{x_Q - x_P} = \frac{6 + 4}{8 - 3} = 2$. Im Anschluss erhältst du durch Einsetzen des Punktes $P$ oder $Q$ entweder $-4 = 2 \cdot 3 + b$ oder $6 = 2 \cdot 8 + b$. Die Auflösung einer der beiden Gleichungen nach $b$ liefert $b = -10$, sodass du schließlich die Funktionsgleichung $f(x) = 2x - 10$ erhältst.

Wenn du nach der zweiten Variante vorgehen möchtest, stellst du mithilfe der beiden Punkte $P$ und $Q$ ein lineares Gleichungssystem zweier Gleichungen, jeweils mit den beiden Unbekannten $m$ und $b$ auf. Dann erhältst du die beiden Gleichungen $-4 = m \cdot 3 + b$ und $6 = m \cdot 8 + b$. Ziehe nun die Gleichungen voneinander ab, sodass du $b$ eliminieren kannst. Bestimme nun mithilfe der Auflösung nach $m$ die Unbekannte $m = 2$. Setze nun ein eine der beiden Gleichungen dein Ergebnis für $m$ ein und bestimme dann mithilfe der Auflösung nach $b$ die Unbekannte $b = -10$. Damit erhältst du schließlich die Funktionsgleichung $f(x) = 2x - 10$.

b) Gegeben seien die Punkte $P(2/1)$ und $Q(6/-5)$.

Lösung

Wenn du nach der ersten Variante vorgehen möchtest, also erst die Steigung $m$ und dann mithilfe eines der beiden Punkte $b$ bestimmen möchtest, dann ergibt sich zunächst für die Steigung: $m = \frac{f(x)_Q - f(x)_P}{x_Q - x_P} = \frac{(-3) - 4}{11 - (-7)} = \frac{-7}{18}$. Im Anschluss erhältst du durch Einsetzen des Punktes $P$ oder $Q$ entweder $4 = \frac{-7}{18} \cdot (-7) + b$ oder $-3 = \frac{-7}{18} \cdot 11 + b$. Die Auflösung einer der beiden Gleichungen nach $b$ liefert $b = \frac{23}{18}$, sodass du schließlich die Funktionsgleichung $f(x) = \frac{-7}{18}x + \frac{23}{18}$ erhältst.

Wenn du nach der zweiten Variante vorgehen möchtest, stellst du mithilfe der beiden Punkte $P$ und $Q$ ein lineares Gleichungssystem zweier Gleichungen, jeweils mit den beiden Unbekannten $m$ und $b$ auf. Dann erhältst du die beiden Gleichungen $4 = m \cdot (-7) + b$ und $-3 = m \cdot 11 + b$. Ziehe nun die Gleichungen voneinander ab, sodass du $b$ eliminieren kannst. Bestimme nun mithilfe der Auflösung nach $m$ die Unbekannte $m = \frac{-7}{18}$. Setze nun ein eine der beiden Gleichungen dein Ergebnis für $m$ ein und bestimme dann mithilfe der Auflösung nach $b$ die Unbekannte $b = \frac{23}{18}$. Damit erhältst du schließlich die Funktionsgleichung $f(x) = \frac{-7}{18}x + \frac{23}{18}$.

c) Gegeben seien die Punkte $P(-7/4)$ und $Q(11/-3)$.

Lösung

Wenn du nach der ersten Variante vorgehen möchtest, also erst die Steigung $m$ und dann mithilfe eines der beiden Punkte $b$ bestimmen möchtest, dann ergibt sich zunächst für die Steigung: $m = \frac{f(x)_Q - f(x)_P}{x_Q - x_P} = \frac{(-3) - 4}{11 - (-7)} = \frac{-7}{18}$. Im Anschluss erhältst du durch Einsetzen des Punktes $P$ oder $Q$ entweder $4 = \frac{-7}{18} \cdot (-7) + b$ oder $-3 = \frac{-7}{18} \cdot 11 + b$. Die Auflösung einer der beiden Gleichungen nach $b$ liefert $b = \frac{23}{18}$, sodass du schließlich die Funktionsgleichung $f(x) = \frac{-7}{18}x + \frac{23}{18}$ erhältst.

Wenn du nach der zweiten Variante vorgehen möchtest, stellst du mithilfe der beiden Punkte $P$ und $Q$ ein lineares Gleichungssystem zweier Gleichungen, jeweils mit den beiden Unbekannten $m$ und $b$ auf. Dann erhältst du die beiden Gleichungen $4 = m \cdot (-7) + b$ und $-3 = m \cdot 11 + b$. Ziehe nun die Gleichungen voneinander ab, sodass du $b$ eliminieren kannst. Bestimme nun mithilfe der Auflösung nach $m$ die Unbekannte $m = \frac{-7}{18}$. Setze nun ein eine der beiden Gleichungen dein Ergebnis für $m$ ein und bestimme dann mithilfe der Auflösung nach $b$ die Unbekannte $b = \frac{23}{18}$. Damit erhältst du schließlich die Funktionsgleichung $f(x) = \frac{-7}{18}x + \frac{23}{18}$.

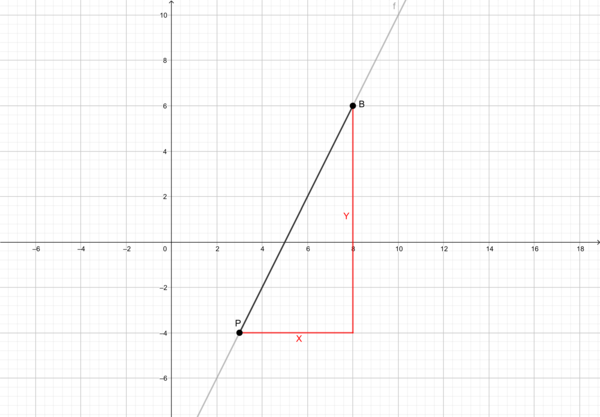
Steigungsdreieck einer linearen Funktion an zwei ausgewählten Punkten