Benutzer:Buss-Haskert/Projekt Mein Traumzimmer/Bodenbelag: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 171: | Zeile 171: | ||
=== Wiederholung: Flächeninhalt von Rechteck und Quadrat === | === Wiederholung: Flächeninhalt von Rechteck und Quadrat === | ||
Link zum Applet https://www.geogebra.org/m/mr3T3Tde | |||
<ggb_applet id="FexywbYW" width="900" height="550" border="888888" /> | |||
<small>Applet von Pöchtrager</small><br> | |||
{{#ev:youtube|GMg5KPRglVY|800|center}} | |||
{{Box|1=Flächeninhalt A|2=<div class="grid"> | |||
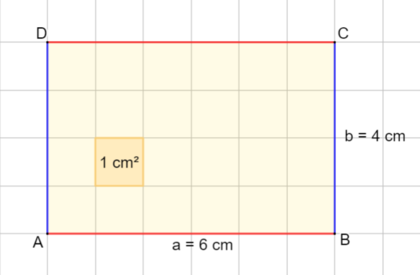
<div class="width-1-2">'''Flächeninhalt A eines Rechtecks'''<br> | |||
[[Datei:Rechteck für Flächeninhalt Merkkasten.png|rahmenlos|420x420px]]<br> | |||
<big>'''Formel: A = a · b'''</big><br> | |||
= 6 cm · 4 cm<br> | |||
= 24 cm² | |||
</div> | |||
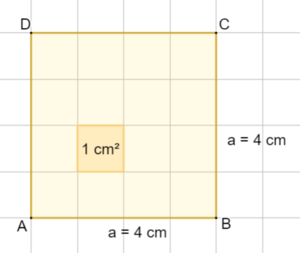
<div class="width-1-2">'''Flächeninhalt Quadrat'''<br> | |||
[[Datei:Quadrat Flächeninhalt Merkkasten.png|rahmenlos|300x300px]]<br> | |||
'''<big>Formel: A = a · a</big>'''<br> | |||
'''<big>= a²</big>'''<br> | |||
= 4 cm · 4 cm<br> | |||
= 16 cm²</div> | |||
</div>|3=Arbeitsmethode}} | |||
{{Box|Übung 1|Bearbeite die nachfolgenden Übungen.|Üben}} | |||
Originallink https://www.geogebra.org/m/dxJkcWyy<br> | |||
<ggb_applet id="dxJkcWyy" width="900" height="550" border="888888" /> | |||
Originallink https://www.geogebra.org/m/rdHqJ9vV | |||
<ggb_applet id="rdHqJ9vV" width="900" height="550" border="888888" /> | |||
Originallink https://www.geogebra.org/m/MH6JeMyY | |||
<ggb_applet id="MH6JeMyY" width="935" height="527" border="888888" /> | |||
<small>Applets von Pöchtrager</small><br> | |||
{{Box|Übung 2|Bearbeite auf der Seite realmath die nachfolgenden Übungen. Sammle jeweils mindestens 300 Punkte. | |||
* [https://realmath.de/Neues/Klasse5/umfang/rechtecksflaeche01.php Aufgabe 1] | |||
* [https://realmath.de/Neues/Klasse5/umfang/rechtecksflaeche.php Aufgabe 2] | |||
* [https://realmath.de/Neues/Klasse5/umfang/rechtecksflaeche2.php Aufgabe 3] | |||
* [https://realmath.de/Neues/Klasse5/umfang/rechteckneu.php Aufgabe 4]|Üben}} | |||
{{Box|Übung 3|Berechne im Applet, wie viele Fliesen benötigt werden.|Üben}} | |||
Originallink https://www.geogebra.org/m/ZsY4uS3j | |||
<ggb_applet id="ZsY4uS3j" width="1024" height="768" border="888888" /> | |||
<small>Applet von B.Zauner</small><br> | |||
{{Box|1=Übung 4|2= | |||
*[https://www.matheaufgaben.net/mathe-online/?Aufgabentyp=Umfang-Flaeche-Quadrat-Rechteck Matheaufgabennet]|3=Üben}} | |||
{{Box|1=Übung 5 - im Heft|2=Zeichne das Rechteck (mit Bleistift und Lineal) und berechne den Flächeninhalt wie im Merkkasten oben.<br> | |||
<div class="grid"> | |||
<div class="width-1-3">a) a = 4 cm; b = 5 cm</div> | |||
<div class="width-1-3">b) a = 8 cm; b = 3 cm</div> | |||
<div class="width-1-3">c) a = 10 cm; b = 1 cm</div> | |||
</div> | |||
|3=Üben}} | |||
{{Box|Übung 6 - Umfang oder Flächeninhalt?|Entscheide in der nachfolgenden App, ob der Umfang oder der Flächeninhalt der Vierecke gesucht ist.|Üben}} | |||
{{LearningApp|app=27645|width=100%|heigth=600px}} | |||
=== Flächeninhalt zusammengesetzter Figuren === | === Flächeninhalt zusammengesetzter Figuren === | ||
{{Box|Übung 7 - Flächeninhalt von Figuren|Berechne den Flächeninhalt der Figuren auf der Seite realmath. (Tipp: Zerlege die Figur in Rechtecke). | |||
*[https://realmath.de/Neues/Klasse5/umfang/rechteckflaechevar.php Aufgabe 1] | |||
*[https://realmath.de/Neues/Klasse5/flaeche/rechteckflaech.php Profilevel] | |||
*[https://realmath.de/Neues/Klasse5/umfang/figurvariabel.php Profilevel Umfang und Flächeninhalt] | |||
|Üben}} | |||
===3. Fußbodenbelag und Deckenfarbe=== | |||
{{Box|Aufgabe 3: Fußbodenbelag und Deckenfarbe|Welchen Fußbodenbelag erhält dein Traumzimmer? Wie wird die Decke gestrichen? | |||
* Wie viele Quadratmeter Fußbodenbelag benötigst du für dein Zimmer? | |||
* Wie viele Quadratmeter groß ist die Decke, die gestrichen werden muss? | |||
* Erkundige dich in einem Geschäft, in Prospekten oder im Internet nach dem Preis für deinen Belag und die Farbe und berechne, wie viel Euro du dafür bezahlen müsstest. | |||
* Notiere deine Rechnungen übersichtlich auf einem Blatt und klebe, falls möglich, Prospektausschnitte dazu. | |||
* Hefte das Blatt in deinen Ordner für das Projekt Mein Traumzimmer. | |||
|Üben}} | |||
Version vom 25. April 2025, 13:39 Uhr
3. Fußbodenbelag und Deckenfarbe
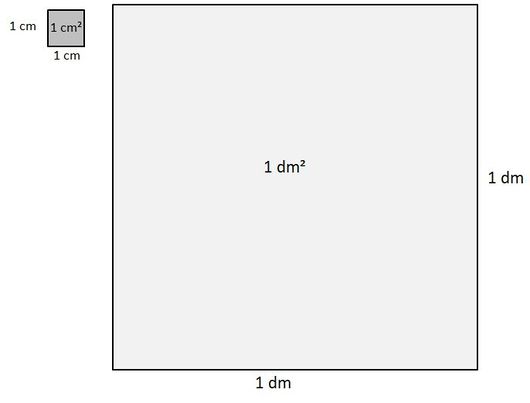
Flächeneinheiten kennenlernen
Originallink https://www.geogebra.org/m/pvy25pcd

Applet des FLINK-Teams
Kontrolliere deine Lösungen mithilfe der LearninApp:
Kontrolliere deine Lösungen mithilfe der LearninApp:
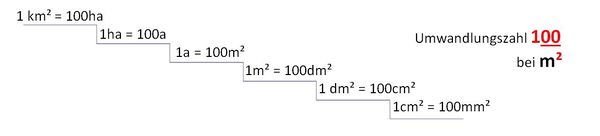
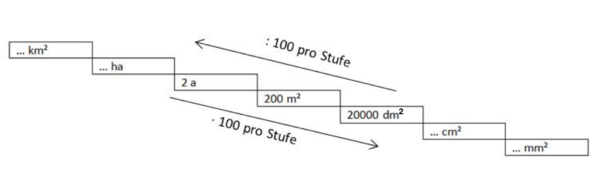
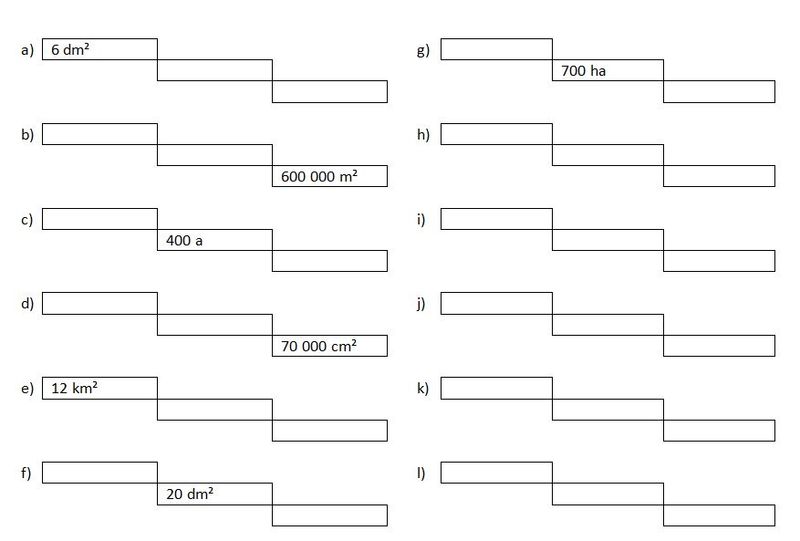
Flächeneinheiten umwandeln
Klicke auf das Bild: Was beobachtest du?


Originallink https://www.geogebra.org/m/cbw6ruke

Applet des FLINK-Teams
Nr. 3a) 24m² = 24·100dm² = 2400dm², denn 1m² = 100dm²
Nr. 4a)500cm² = 500:100dm² = 5dm², denn 100cm²=1dm²
Nr. 5a) 70000cm² = 700dm² = 7m², denn 100cm² = 1dm² und 100dm² = 1m²
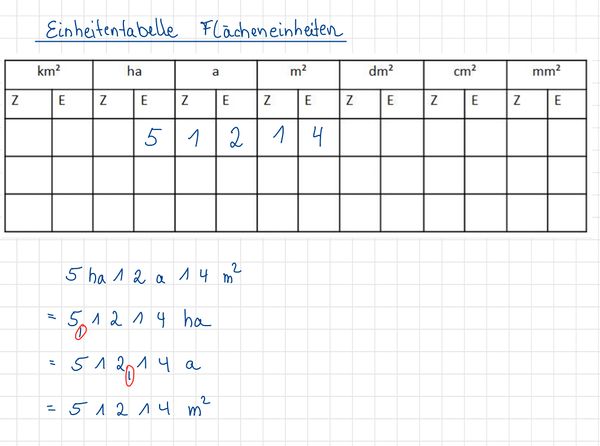
{{Box|Flächeneinheiten - Einheitentabelle|Das riesige Außengelände des Freibades hat folgenden Flächeninhalt:
2ha 12a 14m²
- Trage diese Fläche in die Einheitentabelle ein.
- Gib die Fläche in ha, a und in m² an. Vergleiche dein Ergebnis mit dem deines Partners/deiner Partnerin.
[[Datei:Einheitentabelle Flächeneinheiten.jpg|rahmenlos|600x600p
Originallink https://www.geogebra.org/m/cntgvm9k

Applet des FLINK-Teams
Originallink https://www.geogebra.org/m/wgvcpv58

Applet des FLINK-Teams
Originallink https://www.geogebra.org/m/ahjjmydh

Applet des FLINKE-Teams
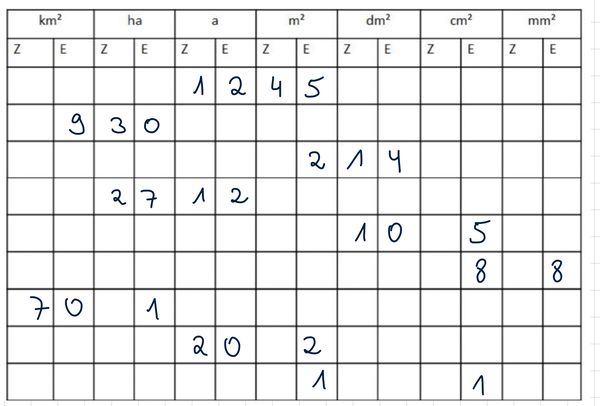
Vermischte Übungen:
Wandle die Ausgangsgröße in die zu ergänzende Größe um:
1m² = 100dm²; 100dm² - 90dm² = 10dm²
1m² = 10000cm²; 10000cm² - 200cm² = ...
Rechnen mit Flächeninhalten
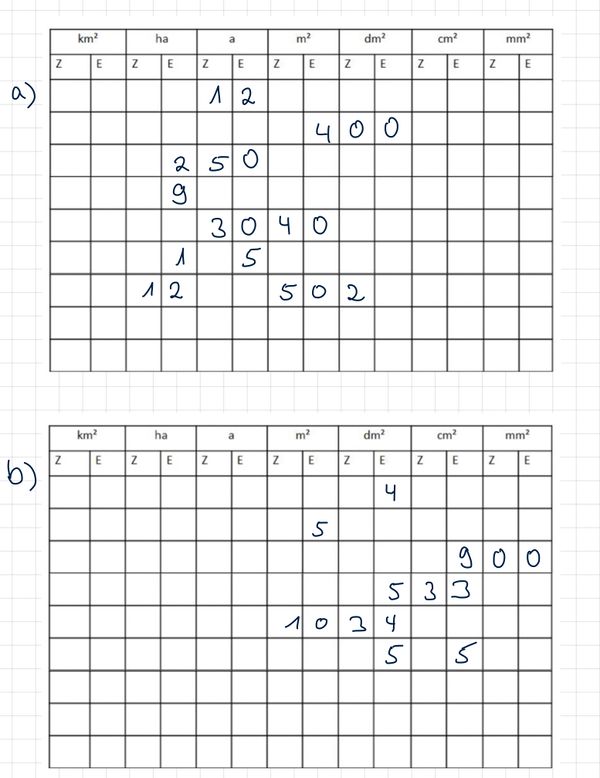
Wandle jeweils in die kleinere Einheit um. Umwandlungszahl bei Flächeninhalten: 100! Addiere bzw. subtrahiere danach.
Erinnerung: 100 dm² = 1m² (Plakat im Klassenraum)
a) 5dm² = 500cm²; 3a = 300 m²
b) 7,2 dm² = 720cm²; 61,3 ha = 6130a
Wandle in die nächstkleinere Einheit um, damit du die Flächen ohne Komma schreiben kannst.
Umwandlungszahl bei Flächeninhalten: 100! Multipliziere bzw. Dividiere anschließend.
Erinnerung: 100 dm² = 1m² (Plakat im Klassenraum)
Wiederholung schriftlich multiplizieren und dividieren:
Flächeneinheiten runden
34,45 m² ≈ 34 m²; 19,38 a ≈ 19 a; 15,87 m² ≈ 16m²
Wiederholung: Flächeninhalt von Rechteck und Quadrat
Link zum Applet https://www.geogebra.org/m/mr3T3Tde

Applet von Pöchtrager
Originallink https://www.geogebra.org/m/dxJkcWyy

Originallink https://www.geogebra.org/m/rdHqJ9vV

Originallink https://www.geogebra.org/m/MH6JeMyY

Applets von Pöchtrager
Originallink https://www.geogebra.org/m/ZsY4uS3j

Applet von B.Zauner