Geometrie im Dreieck/Komm zum Punkt

Du hast dich nach Bearbeitung der Diagnoseaufgaben entschlossen, dein Wissen über charakteristische Punkte des Dreiecks aufzufrischen.

Information

In diesem Lernpfadkapitel werden besondere Punkte eines Dreiecks behandelt.

Bei diesen Punkten handelt es sich um den Umkreismittelpunkt, den Inkreismittelpunkt und den Schwerpunkt. In deinem Mathebuch findest du das Thema auf den Seiten 56, 57 und 64. Um dieses Kapitel bearbeiten zu können, müssen die Winkelhalbierende, die Seitenhalbierende und die Mittelsenkrechte eines Dreiecks konstruiert werden können. Wenn du dir da noch unsicher bist, schaue dir dieses Kapitel an.

Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in pinker Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit lilanem Streifen sind Knobelaufgaben.

Viel Erfolg!

Einbrecher in Münster

Ganz Münster ist in Angst versetzt. Einbrecher sind in der Stadt unterwegs. Doch Kommissar Biehl hat eine heiße Spur: er kann eingrenzen, wo der nächste Einbruch stattfinden wird. Dafür kommen zwei Juweliere und eine Bank infrage.

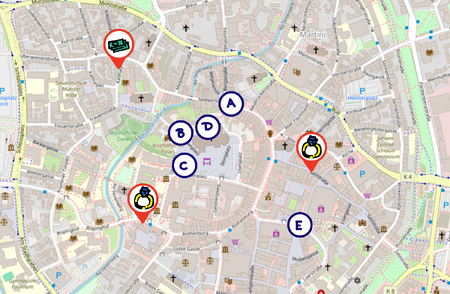
Kommissar Biehl muss natürlich schnellstmöglich vor Ort sein, um die Einbrecher auf frischer Tat zu ertappen. Wo soll er sich heute Nacht in der Stadt aufhalten, damit er schnell an jedem möglichen Einbruchsort sein kann?

In diesem Kapitel wollen wir Kommissar Biehl helfen, mithilfe von Mathematik einen guten Ort zu finden. Dafür erinnert er sich daran, was er in der Schule zu besonderen punkten im Dreieck gelernt hat.“

Wissen I

Aus den Mittelsenkrechten wird der Umkreismittelpunkt konstruiert.

Der Kreis, der alle Eckpunkte eines Dreiecks berührt, heißt Umkreis. Der Umkreismittelpunkt ist der Schnittpunkt der drei Mittelsenkrechten des Dreiecks. Zur Konstruktion des Umkreises genügt es, zwei Mittelsenkrechten zu konstruieren, die dritte schneidet im selben Punkt.

Du weißt über Mittelsenkrechten aus dem letzten Kapitel:

Alle Punkte auf der Mittelsenkrechte haben zu den zugehörigen Eckpunkten den selben Abstand. Als Schnittpunkt aller Mittelsenkrechten haben vom Punkt M alle Ecken somit den selben Abstand. Deswegen kannst du, wenn du den richtigen Radius wählst, um den Schnittpunkt M einen Kreis zeichnen, der alle Eckpunkte durchläuft. Das ist der Umkreis.

Der Inkreis, konstruiert aus den Winkelhalbierenden.

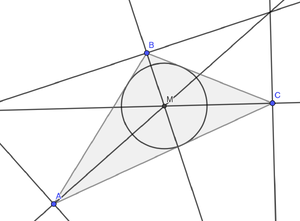
Der Kreis, der alle Seiten eines Dreiecks genau einmal berührt, heißt Inkreis. Der Inkreismittelpunkt ist der Schnittpunkt der drei Winkelhalbierenden des Dreiecks. Auch hier genügen zwei Winkelhalbierende zur Konstruktion des Kreises.

Du weißt: Punkte auf der Winkelhalbierenden haben von den beiden Seiten, die den Winkel einschließen, die selbe kürzeste Entfernung. Auch hier: Vom Schnittpunkt aller Winkelhalbierenden sind alle Seiten gleich weit entfernt. Wenn du einen Kreis zeichnest, der eine Seite in einem Punkt berührt (der Inkreis), dann berührt er auch die anderen Seiten in nur einem Punkt.

Der Schwerpunkt eines Dreiecks, Schnittpunkt der Seitenhalbierenden.

Der Schwerpunkt eines Kreises ist der Schnittpunkt der Seitenhalbierenden. Auf einer Seitenhalbierenden liegt der Schwerpunkt immer auf 2/3 der Strecke vom Eckpunkt bis zur gegenüberliegenden Seite.

Wenn du aus einem gleichmäßigen Material ein Dreieck ausschneidest, müsstest du es auf dem Schwerpunkt balanieren können.

Merksatz

Aufgabe 1:

Vervollständige den Merksatz und kontrolliere deine Lösung. Schreibe dir den Merksatz auch in deinen Unterlagen auf!

Übung

Aufgabe 2:

a) Bilde Paare aus den dargestellten Konstruktionen und den notwendigen Linien.

b) Wie kannst du dir gut merken, welcher Punkt zu welchen Geraden gehört? Notiere hierzu eine Eselsbrücke oder eine andere Merktechnik zu den drei Punkten.

Eine einfache Eselsbrücke könnte so lauten:

Schwerpunkt und Seitenhalbierende: Beides beginnt mit "S".

Inkreis und Winkelhalbierende: In beidem kommt "ink" vor.

Umkreis und Mittelsenkrechte: In beidem kommt "m" vor.

Konstruktion

Wie Kommissar Biehl, solltest auch du auf alle möglichen Punkte im Dreieck vorbereitet sein. Probiere dich an allen Kontruktionsaufgaben aus, wenn du Hilfe brauchst, kannst du dir die Kontruktionsschritte anzeigen lassen.

Aufgabe 3 a): Umkreis

Konstruiere mittels der in Geogebra gegebenen Werkzeuge den Umkreis des gegebenen Dreiecks.

Aufgabe 3 b): Inkreis

Konstruiere den Inkreis des gegebenen Dreiecks.

Aufgabe 3 c): Schwerpunkt

Konstruiere den Schwerpunkt des gegebenen Dreiecks.

Wissen II

Kommissar Biehl hat einen anonymen Tipp erhalten, die ihm beim Umgang mit dem Umkreismittelpunkt helfen. Der Umkreismittelpunkt kann als einziger Punkt auch außerhalb des Dreiecks liegen. Nämlich genau dann, wenn das Dreieck einen stumpfen Winkel hat. Bei einem rechtwinkligen Dreieck liegt der Umkreismittelpunkt auf der gegebüberliegenden Seite (Hypotenuse). Im Applet kannst du die Eckpunkte des Dreiecks verschieben und den Umkreismittelpunkt beobachten.

Wenn du nicht mehr weißt was ein stumpfer Winkel ist schaue hier.

Fällt dir bei einem rechtwinkligen Dreieck etwas auf? Wenn du deine Beobachtung zuhause vertiefen möchtest, schau dir doch mal den Satz des Thales an.

Vertiefung

Kommissar Biehl möchte sich absolut sicher sein, welcher Standort der beste für ihn ist, muss sich aufgrund des Zeitdrucks aber auf eine Aufgabe beschränken. Wähle eine der nächsten beiden Aufgaben zur Bearbeitung.

Aufgabe 4:

Sortiere die Eigenschaften und Darstellungen den Punkten des Dreiecks zu. Wenn du auf die Bilder klickst, werden sie groß.

Aufgabe 5:

Benenne die Punkte M₁ M₂ und M₃ der dynamischen Grafik. Du kannst die Eckpunkte des Dreiecks bewegen.

Tippe eine Ecke des Dreiecks an und verschiebe sie. Wie bewegen sich die gekennzeichneten Mittelpunkte?

Schaffst du es das Dreieck so zu bewegen, dass ein Punkt außerhalb des Dreiecks liegt? Welcher Punkt kann das nur sein?

Stell dir eine Winkelhalbierende vor. Welcher der Punkte könnte der Schnittpunkt mehrerer Winkelhalbierender sein.

Auf der Lauer

Aufgabe 6: Entfernungsproblem

Finde den Ort an dem Kommissar Biehl warten soll, damit er gleich schnell bei jedem möglichen Einbruchsort ist. Dabei ist das Straßennetz egal, es zählt nur die Entfernung zum Ziel. Du kannst im Fenster mit Geogebra Konstruktionen durchführen.

Kommissar Biehl sollte von jedem Einbruchsort gleichweit entfernt sein.

Der Umkreismittelpunkt ist von jedem Eckpunkt eines Dreiecks gleich weit entfernt.

Super, du hast es geschafft! Hier findest du zurück zum Ausgangspunkt der Stunde: Geometrie im Dreieck