|
|
| Zeile 17: |
Zeile 17: |
| ==Aufgabe 1: Zuordnungen von Begriffen zu Abbildungen== | | ==Aufgabe 1: Zuordnungen von Begriffen zu Abbildungen== |
|
| |
|
| | {{Box|Merksatz: Scheitelwinkel||Merksatz |
| | }} |
| | |
| | An zwei Geraden, die sich schneiden, nennt man gegenüberliegende Winkel '''Scheitelwinkel'''. Die Winkel sind gleich groß. In der Abbildung: α und β sind Scheitelwinkel und es gilt α = β. |
|
| |
|
| {{Box|Merksatz: Scheitelwinkel
| |
| | An zwei Geraden, die sich schneiden, nennt man gegenüberliegende Winkel '''Scheitelwinkel'''. Die Winkel sind gleich groß.
| |
|
| |
|
| In der Abbildung: α und β sind Scheitelwinkel und es gilt α = β.|Merksatz
| |
| }}
| |
| ==Aufgabe 2: Winkelgrößen bestimmen== | | ==Aufgabe 2: Winkelgrößen bestimmen== |
| ===Schwierigkeitsstufe I=== | | ===Schwierigkeitsstufe I=== |
| Zeile 52: |
Zeile 52: |
| | Farbe = {{Farbe|orange}} | | | Farbe = {{Farbe|orange}} |
| }} | | }} |
| === Schwierigkeitsstufe II=== | | ===Schwierigkeitsstufe II=== |
| {{Box|Aufgabe 2: Winkelgrößen bestimmen|Bestimme die Winkelgrößen und begründe mit Hilfe der Winkeltypen, wie du auf die Lösung gekommen bist. | | {{Box|Aufgabe 2: Winkelgrößen bestimmen|Bestimme die Winkelgrößen und begründe mit Hilfe der Winkeltypen, wie du auf die Lösung gekommen bist. |
|
| |
|
| Zeile 122: |
Zeile 122: |
| ===Winkeltyp 1=== | | ===Winkeltyp 1=== |
| Mein Nachbarwinkel und ich bilden gemeinsam eine gestreckte Linie. Wir ergänzen und immer zu einem Halbkreis. Wer bin ich? | | Mein Nachbarwinkel und ich bilden gemeinsam eine gestreckte Linie. Wir ergänzen und immer zu einem Halbkreis. Wer bin ich? |
| {{Lösung versteckt|1=Je größer mein Nachbarwinkel ist, desto kleiner bin ich.|2=Tipp 1|3=Tipp 1}}
| |
| {{Lösung versteckt|1=Mein Nachbarwinkel und ich ergeben gemeinsam 180 Grad. Wenn er beispielsweise 70 Grad aufweist, besitze ich 110 Grad.|2=Tipp 2|3=Tipp 2}}
| |
| {{Lösung versteckt|1=Ich bin der Nebenwinkel.|2=Lösung|3=Lösung}}
| |
|
| |
|
| ===Winkeltyp 2=== | | ===Winkeltyp 2=== |
| Zeile 148: |
Zeile 145: |
| {{ | | {{ |
| Lösung versteckt|Tipp| | | Lösung versteckt|Tipp| |
| Erster Tipp
| | Tipp |
| |Tipp verbergen
| |
| }}
| |
| | |
| {{
| |
| Lösung versteckt|Tipp|
| |
| Zweiter Tipp
| |
| |Tipp verbergen | | |Tipp verbergen |
| }} | | }} |
Kapitel-Informationskästchen
Info
In diesem Lernpfadkapitel beschäftigen wir uns mit den verschiedenen Winkelarten: dem Neben-, Scheitel-, Stufen- und Wechselwinkel.
Du hast noch Unsicherheiten, wann welcher Winkel vorliegt? Hast Schwierigkeiten sie zu erkennen? Oder die nützlichen Eigenschaften, die mit den verschiedenen Winkeln einhergehen, sind dir noch nicht vollends bewusst? Dann bist du hier genau richtig. Wir lernen das gemeinsam.
Bei den Aufgaben unterscheiden wir folgende Typen:
- In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
- Aufgaben in pinker Farbe sind Aufgaben mittlerer Schwierigkeit.
- Und Aufgaben in lilaner Farbe sind Knobelaufgaben.
Viel Erfolg!
Aufgabe 1: Zuordnungen von Begriffen zu Abbildungen
An zwei Geraden, die sich schneiden, nennt man gegenüberliegende Winkel Scheitelwinkel. Die Winkel sind gleich groß. In der Abbildung: α und β sind Scheitelwinkel und es gilt α = β.
Aufgabe 2: Winkelgrößen bestimmen
Schwierigkeitsstufe I
Aufgabe 2: Winkelgrößen bestimmen
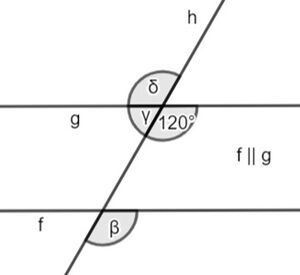
Bestimme die Winkelgrößen und begründe mit Hilfe der Winkeltypen, wie du auf die Lösung gekommen bist.
β=120°
mögliche Begründung:
- 1. β ist Stufenwinkel zum Winkel 120°. Da Stufenwinkel gleich groß sind, gilt β=120°.
- 2. Falls δ=120° schon bestimmt wurde: β=120°, da β und δ Wechselwinkel sind und diese gleich groß sind.
γ=60°
mögliche Begründungen:
- 1. γ ist Nebenwinkel zum Winkel 120°. Da γ+120°=180° gelten muss, ist γ=60°.
- 2. γ ist Nebenwinkel zu δ=120°. Wegen γ+120°=180° gilt dann γ=60°.
δ=120°
mögliche Begründungen:
- 1. δ ist Scheitelwinkel zu 120° und Scheitelwinkel sind immer gleich groß. Also ist δ=120°.
- 2. Falls γ=60° schon bestimmt wurde: δ ist Nebenwinkel zu γ=60°. Weil γ+δ=180° sein muss, ist δ=120°.
- 3. Falls β=120° schon bestimmt wurde: Da β und δ Wechselwinkel sind, sind sie gleich groß und es gilt δ=120°.
Schwierigkeitsstufe II
Aufgabe 2: Winkelgrößen bestimmen
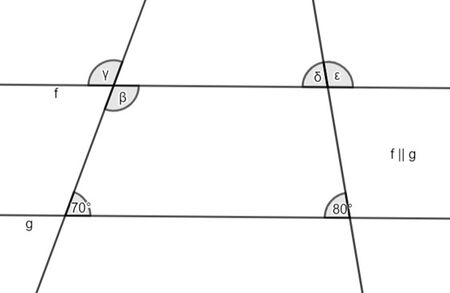
Bestimme die Winkelgrößen und begründe mit Hilfe der Winkeltypen, wie du auf die Lösung gekommen bist.
α=70°
mögliche Begründung:
- α ist Stufenwinkel zum Winkel 70°. Da Stufenwinkel gleich groß sind, gilt α=70°.
β=110°
mögliche Begründungen:
- 1. α und β sind Nebenwinkel, also muss α+β=180° gelten. Da α=70° ist, muss β=110° sein.
- 2. Falls γ schon bestimmt wurde: β ist Scheitelwinkel zu γ=110°. Da Scheitelwinkel gleich groß sind, gilt β=110°.
γ=110°
mögliche Begründungen:
- 1. α und γ sind Nebenwinkel, also muss α+γ=180° gelten. Da α=70° ist, muss γ=110° sein.
- 2. Falls β schon bestimmt wurde: γ ist Scheitelwinkel zu β=110°. Da Scheitelwinkel gleich groß sind, gilt γ=110°.
δ=80°
mögliche Begründung:
- δ ist Stufenwinkel zu 80°. Da Stufenwinkel gleich groß sind, ist auch δ=80°.
ε=100°
mögliche Begründung:
- ε ist Nebenwinkel zu δ=80°. Da δ+ε=180° gelten muss, ist ε=100°.
Schwierigkeitsstufe III
Aufgabe 2: Winkelgrößen bestimmen
Bestimme die Winkelgrößen und begründe mit Hilfe der Winkeltypen, wie du auf die Lösung gekommen bist.
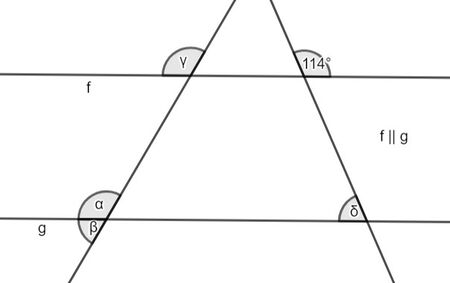
Winkel α ist doppelt so groß wie Winkel β.
α=120° und β=60°
mögliche Begründung:
- α und β sind Nebenwinkel, weshalb α+β=180° gelten muss. Da α doppelt so groß ist wie β, folgt daraus, dass α=120° und β=60° ist.
γ=120°
mögliche Begründung:
- Da γ Stufenwinkel zu α=120° ist und Stufenwinkel gleich groß sind, gilt γ=120°.
δ=66°
mögliche Begründung:
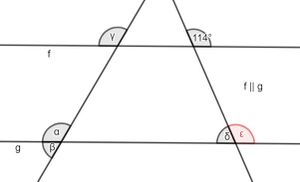
- Man kann einen Stufenwinkel zum Winkel 114° einzeichen, der Nebenwinkel zum Winkel δ ist (Winkel ε in der Abbildung rechts). Da Stufenwinkel gleich groß sind, ist ε=114°. Mit δ+ε=180° folgt dann δ=66°.
Aufgabe 3: Wer bin ich?
Winkeltyp 1
Mein Nachbarwinkel und ich bilden gemeinsam eine gestreckte Linie. Wir ergänzen und immer zu einem Halbkreis. Wer bin ich?
Winkeltyp 2
Winkeltyp 3
Winkeltyp 4
Aufgabe 4: Winkel in der Sporthalle
Bild
Aufgabe 1: Zeichnen
Zeichne die Sprossenwand, die Bänke, den großen Kasten und die Linie (auf dem Boden) als Geraden in dein Heft. Übertrage außerdem die Winkel aus dem Foto in deine Zeichnung. (z.B. zwischen Bank und Sprossenwand).
Aufgabe 2: Winkel benennen und berechnen
Benenne die Winkeltypen, die in der Darstellung auftauchen und berechne deren Größe.
Tipp
Lösung