Geometrie im Dreieck/Mehr als eine Linie: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 147: | Zeile 147: | ||
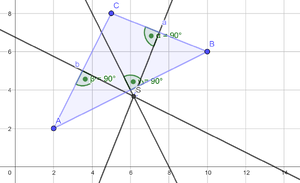
{{Lösung versteckt|Nutze die Mittelsenkrechten.| 2. Tipp anzeigen | 2. Tipp verbergen}} | {{Lösung versteckt|Nutze die Mittelsenkrechten.| 2. Tipp anzeigen | 2. Tipp verbergen}} | ||
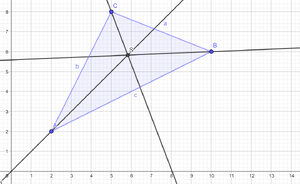
{{Lösung versteckt|Die richtige Lösung findest du [https://www.geogebra.org/calculator/x7krntjr hier].| Lösung anzeigen | Lösung verbergen}} | |||
b) Beurteile, ob dieses Modell realitätsnah ist und welche Vereinfachungen du angenommen hast. | b) Beurteile, ob dieses Modell realitätsnah ist und welche Vereinfachungen du angenommen hast. | ||
|Arbeitsmethode| Farbe={{Farbe|grau}} }} | |Arbeitsmethode| Farbe={{Farbe|grau}} }} | ||