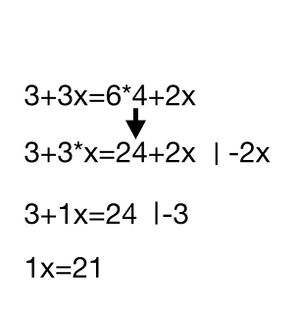|
|
| Zeile 241: |
Zeile 241: |
| #Jetzt wendet man die Äquivalenzumformung an | | #Jetzt wendet man die Äquivalenzumformung an |
| #Wenn dann alle Zahlen auf der einen Seite sind und alle Variablen auf der anderen, muss durch multiplizieren und dividieren die Variable bestimmt werden.(vor der Variable muss eine 1 stehen) | | #Wenn dann alle Zahlen auf der einen Seite sind und alle Variablen auf der anderen, muss durch multiplizieren und dividieren die Variable bestimmt werden.(vor der Variable muss eine 1 stehen) |
| #|Farbe= #0077dd |Hintergrund= #54ff9f| }} | | #|Farbe= #0077dd |Hintergrund= #54ff9f| }} |
Version vom 8. November 2023, 09:35 Uhr
Brüche
Definition
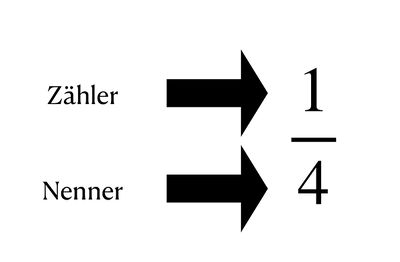
Ein Bruch besteht aus einem Zähler (die Zahl oben) und einem Nenner (die Zahl unten). Der Bruchstrich ist die Linie dazwischen.Er trennt Zähler und Nenner.Sie sind immer natürliche Zahlen, wobei der Nenner niemals die Zahl 0 sein darf.
Mit Brüchen bezeichnest du einen Teil eines Ganzen.
Gemischter Bruch
Ist der Zähler größer als der Nenner, so kann man den Bruch in einen gemischten Bruch umwandeln.
Tutorial
- Wie oft passt der Nenner in den Zähler.
- Das Ergebnis vor den Bruch schreiben.
- Der Rest der Zahl kommt in den Nenner.
Brüche kürzen und erweitern. Wie geht's?
Kürzen
Nenner und Zähler müssen durch die selbe Zahl geteilt werden.
Erweitern
Nenner und Zähler müssen mit der selben Zahl multiplziert werden.
Übung 1: Ordne richtig zu!
Bearbeite die folgende LearningApp: Kürzen 1
Übung 2: Ordne richtig zu!
Bearbeite die folgende LearningApp: Kürzen 2
Wofür brauche ich jetzt eigentlich Brüche und dieses Erweitern und Kürzen?
Nutzen von Brüchen
Mit Brüchen können komplizierte Zahlen wie 0.33333 leichter angegeben und berechnet werden.
In diesem Fall wäre das 1/3.
Mit Brüchen rechnen. Wie soll ich das machen?
Adition
Durch Erweitern und Kürzen müssen die Summanden im Nenner alle dieselbe Zahl haben. Diese wird im Ergebnis auch bin den Zähler geschrieben. Die, durch das Erweitern und Kürzen veränderten Zähler werden miteinander addiert.
Differenz
Ähnlich wie Addition. Alle Brüche müssen denselben Nenner haben. Die Zähler werden miteinander subtrahiert
Multiplikation
Zähler mal Zähler = Zähler im Ergebnis
Nenner mal Nenner = Nenner im Ergebnis
Division
Zähler und Nenner werden im 2. Bruch vertauscht. Danach werden die Brüche multipliziert. Wenn mehrere Brüche miteinander dividiert werden, muss nacheinander vorgegangen werden (Es können nur 2 Brüche gleichzeitig miteinander dividiert werden).
Übung 3: Ordne richtig zu!
Bearbeite die folgende LearningApp: Addition von Brüchen
Übung 4: Ordne richtig zu!
Bearbeite die folgende LearningApp: Subtraktion von Brüchen
Übung 5: Ordne richtig zu!
Bearbeite die folgende LearningApp: Multiplikation von Brüchen
Übung 6: Ordne richtig zu!
Bearbeite die folgende LearningApp: Division von Brüchen
Übung 7: Ordne richtig zu!
Bearbeite die folgende LearningApp: Mit Brüchen rechnen für Fortgeschrittene
Terme und Gleichungen
Was ist das?
Definition Term
Ein Term ist eine sinnvolle Kombination aus Zahlen, Variablen, mathematischen Verknüpfungen(+-*:) und Klammern. Relationszeichen dürfen in Termen nicht vorhanden sein. Ein Term kann nur aus einer Zahl oder Variable bestehen.
Was ist eine Variable?
Eine Variable ist ein Platzhalter für eine Zahl. Wenn zwischen zwei Variablen oder zwischen Zahl und Variable ein Malzeichen steht, kann man das weglassen. Wenn ein Malzeichen vor einer Klammer steht, trifft das auch zu.
Definition Gleichung
Eine Gleichung ist ein mathematischer Ausdruck, bestehend aus zwei Termen, die durch das Gleichheitszeichen verbunden sind.
Übung 1: Ordne richtig zu!
Bearbeite die folgende LearningApp: Terme und Gleichungen
Wie löse ich jetzt Gleichungen?
Gleichung lösen
Eine Gleichung kann durch Probieren oder der Äquivalenzumformung gelöst werden. Das Ziel ist es eine Variable zu bestimmen.
Probieren
Durch systematisches Einsetzen von Zahlen für die Variable kommt man zum Ergebnis. Problem: Dauert zu lange und es können mögliche Ergebnisse verloren gehen.
Äquivalenzumformung
Auf beiden Seiten der Gleichung muss die selbe Operation durchgeführt werden. Dazu schreibt man eine sogenannten Operationsstrich hinter die Gleichung, daneben das Rechenzeichen und da neben die Zahl oder Variable oder beides. Ziel ist es auf eine Seite der Gleichung nur Zahlenterme zu haben und auf der anderen Seite nur die zu bestimmende Variable.
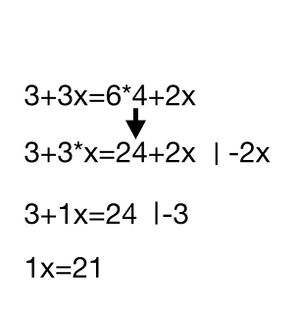
Tutorial
- Zuerst wird alles zusammengefasst, was geht.
- Jetzt wendet man die Äquivalenzumformung an
- Wenn dann alle Zahlen auf der einen Seite sind und alle Variablen auf der anderen, muss durch multiplizieren und dividieren die Variable bestimmt werden.(vor der Variable muss eine 1 stehen)