Benutzer:L.hodankov/Lineare Funktionen/Anwendungsaufgaben: Unterschied zwischen den Versionen
(Formulierungen angepasst) Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 61: | Zeile 61: | ||
{{Box|Übung | {{Box|Übung 3: Tandemsprung|[[Datei:Skydiving-297103 1280.png|mini|<small>Bild von Clker-Free-Vector-Images auf Pixabay</small> ]] | ||
Ein weiteres Angebot im Aktiv-Urlaub ist ein Tandem-Fallschirmsprung. Nach dem Öffnen des Fallschirms misst du mit einem Höhenmesser jede Sekunde deine Höhe über dem Erdboden. | Ein weiteres Angebot im Aktiv-Urlaub ist ein Tandem-Fallschirmsprung. Nach dem Öffnen des Fallschirms misst du mit einem Höhenmesser jede Sekunde deine Höhe über dem Erdboden. | ||
[[Datei:Skydiving Tabelle.png|center]] | [[Datei:Skydiving Tabelle.png|center]] | ||
| Zeile 70: | Zeile 70: | ||
b) Auf welche Höhe befindest du dich nach 6 Sekunden? Löse durch eine Rechnung und prüfe dein Ergebnis am Graphen. | b) Auf welche Höhe befindest du dich nach 6 Sekunden? Löse durch eine Rechnung und prüfe dein Ergebnis am Graphen. | ||
c) Berechne die Fallzeit des | c) Berechne die Fallzeit des Tandem- Sprunges, also wie lange dauert es, bis man wieder auf dem Boden landet. | ||
d) Denke dir selbst eine Aufgabe zum Fallschirmsprung aus.|Üben}} | d) Denke dir selbst eine Aufgabe zum Fallschirmsprung aus.|Üben}} | ||
| Zeile 88: | Zeile 88: | ||
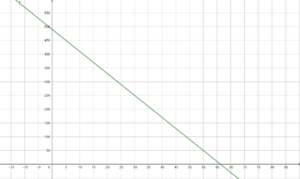
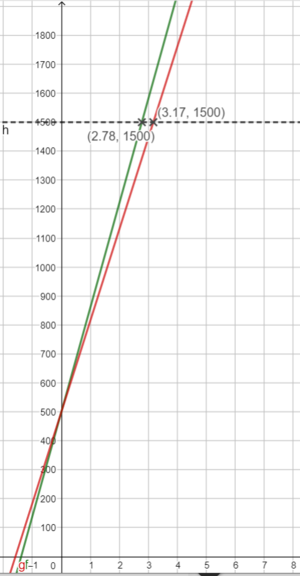
{{Lösung versteckt|1=Wenn man wieder landet, ist die Höhe gleich 0, also gilt f(x) = 0. | {{Lösung versteckt|1=Wenn man wieder landet, ist die Höhe gleich 0, also gilt f(x) = 0. | ||
[[Datei:Graph Fallschirmsprung.png|mini|center]]|2=Tipp zu c)|3=Verbergen}} | [[Datei:Graph Fallschirmsprung.png|mini|center]]|2=Tipp zu c)|3=Verbergen}} | ||
Aktuelle Version vom 18. Oktober 2023, 20:03 Uhr
Diese Seite des Lernpfades wurde teilweise übernommen von der Seite Herta-Lebenstein-Realschule https://projekte.zum.de/wiki/Herta-Lebenstein-Realschule/Lineare_Funktionen_im_Aktiv-Urlaub . Der Autor ist Buss-Haskert. Diese Seite wurde veröffentlicht unter der Lizenz CC BY SA.
Herzlichen Dank!
SEITE IM AUFBAU !!!
Lineare Funktionen im Aktivurlaub und andere Anwendungen
Es gibt Situationen in unserem Alltag, in denen sich Probleme oder Fragen mithilfe von linearen Funktionen beschreiben und lösen lassen. Solche Aufgaben nennen wir "Anwendungsaufgaben". Die Alltagssituation wird in ein mathematisches Modell übertragen, mit unserem Wissen zu den linearen Funktionen mathematisch gelöst und diese Lösung dann auf die Situation bezogen.
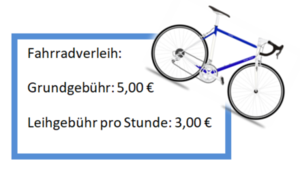
Die Zuordnung lautet Zeit [Stunden] Kosten [€]
x gibt also die Zeit an, f(x) die Kosten.Du hast 20€ zur Verfügung. Also ist y = 20€. Setze dies in die Funktionsgleichung ein und löse die Gleichung nach x auf.
Du benötigst für die Funktionsgleichung die Steigung m und den y-Achsenabschnitt b.
Die Steigung der Funktion ist m = 20, denn in 1 Stunde werden 20 km zurückgelegt.
Der y-Achsenabschnitt beträgt -10, da der Freund 0,5 Stunden später startet, in denen er 10 km zurückgelegt hätte.
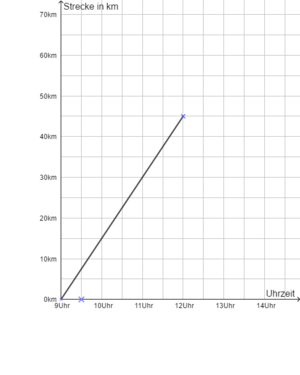
Die Funktionsgleichung lautet f(x) = 20x-10, wobei x die Anzahl der Stunden (nach 9:00 Uhr) angibt.Der Punkt, wann die Freunde sich treffen, ist der Schnittpunkt der beiden Geraden. Hier haben beide Gruppen dieselbe Strecke zurückgelegt, das heißt, sie sind gleich weit gefahren und müssen sich demnach treffen.
Um zu berechnen, wann die Freunde sich treffen, berechne also den Schnittpunkt der Gerden. An dieser Stelle x haben sie dieselben y-Werte, sie sind gleich weit gefahren. Es gilt y = 15x und y=20x-10.
Löse die Gleichung 15x = 20x-10 nach x auf.
Für die Funktionsgleichung benötigst du die Steigung m und den y-Achsenabschnitt b. Wo findest du dies in der Wertetabelle? Den y-Achsenabschnitt liest du bei x=0 ab.
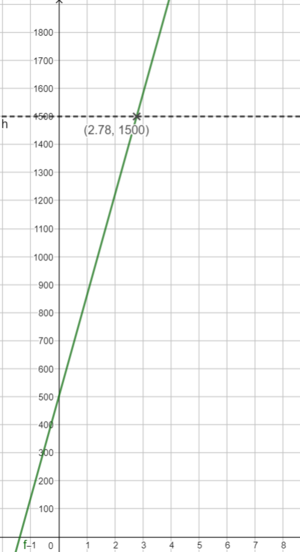
Die Steigung m findest du so: Wenn du bei x eine Einheit nach rechts gehst, gehst du m Einheiten nach oben oder unten. Wie groß ist also die Steigung hier?geg: x=6 Sekunden; f(x) = -8x+490
ges: f(6)
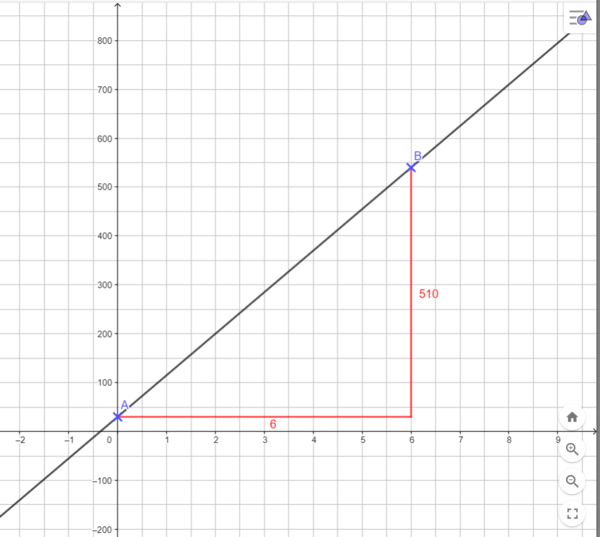
gegeben: 30 km zu Beginn (auf dem Tacho); 540 km nach 6 Stunden
gesucht: Durchschnittsgeschwindigkeit
Was hat dies mit linearen Funktionen zu tun?
Zuordnung: Zeit (h) → Weg (km)
b = 30 (zu Beginn); P(6|540)
f(x) = mx + b
Versuche aus dem Aufgabentext eine Funktionsgleichung nach dem Schema y = mx + b aufzustellen.
- Was stellt x und was y dar?
- x sind die Anzahl der Arbeitswochen.
- y ist der Betrag, den Linus an Geld zur Verfügung hat.
- Welche Bedeutung haben die 500€, die er bereits gespart hat?
- Welche Bedeutung hat der Stundenlohn von 9€?
f(x) = mx + b
b = 500, denn Linus hat schon 500€ gespart.
m = 360, denn pro Stunde kommen 9€ hinzu, ein Arbeitstag hat 8 Stunden und jede Woche hat 5 Arbeitstage, also 9·8·5=360.