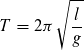Abitur Physik am Gymnasium Trittau/Harmonische Schwingung: Unterschied zwischen den Versionen
GT061 (Diskussion | Beiträge) K (Bild hinzugefügt) Markierung: Quelltext-Bearbeitung 2017 |
GT061 (Diskussion | Beiträge) K (Bilder hinzugefügt) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 3: | Zeile 3: | ||
[[Datei:Schwingungsdauer harmonische Schwingung.png |Schwingungsdauer]] | [[Datei:Schwingungsdauer harmonische Schwingung.png |Schwingungsdauer]] | ||
[[Datei:Kraft harmonische Schwingungen.png |Kraft]] | |||
Wenn man noch eine Dämpfung hat kommt wird noch der Abklingkoeffizient hinzugefügt | Wenn man noch eine Dämpfung hat kommt wird noch der Abklingkoeffizient hinzugefügt | ||
[[Datei:Schwingungsdauer mit Dämpfung.png |Schwingungsdauer]] | |||
| Zeile 12: | Zeile 15: | ||
Ein weiteres Beispiel für eine harmonische Schwingung ist das Fadenpendels, wobei ein Gewicht an einem Faden hängt und es hin und her Schwingt. Hierbei kommt nun die Zentripetalkraft ins Spiel. Mit Hilfe dieser und der Gewichtskraft kann man die Formel für die Kraft der Auslenkung aufstellen | Ein weiteres Beispiel für eine harmonische Schwingung ist das Fadenpendels, wobei ein Gewicht an einem Faden hängt und es hin und her Schwingt. Hierbei kommt nun die Zentripetalkraft ins Spiel. Mit Hilfe dieser und der Gewichtskraft kann man die Formel für die Kraft der Auslenkung aufstellen | ||
[[Datei:Kraft Fandenpendel.png |Kraft]] | |||
Setzt man diese mit der Kraftgleichung einer harmonischen Schwingung gleich, erhält man diese Gleichung | Setzt man diese mit der Kraftgleichung einer harmonischen Schwingung gleich, erhält man diese Gleichung | ||
[[Datei:D.png |D]] | |||
Setz man diese nun in die Gleichung zur Schwingungsdauer ein erhält man abschließend die Gleichung eines Fandenpendels. | Setz man diese nun in die Gleichung zur Schwingungsdauer ein erhält man abschließend die Gleichung eines Fandenpendels. | ||
[[Datei:Schwingungsdauer Fadenpendel.png |Schwingungsdauer]] | |||
<small>Metzler: S.110; Tafelwerk: S.114</small> | <small>Metzler: S.110; Tafelwerk: S.114</small> | ||
Version vom 20. Mai 2023, 08:02 Uhr
Die harmonischen Schwingungen stimmen mit der Projektion einer gleichförmigen Kreisbewegung überein. Damit werden diese Schwingungen auch Sinusschwingungen genannt. Für harmonische Schwingungen gilt die folgende Gleichung für die Schwingungsdauer und die Kraft.
Wenn man noch eine Dämpfung hat kommt wird noch der Abklingkoeffizient hinzugefügt
Ein Beispiel für einen harmonischen Schwinger ist der Federpendel. Hierbei hängt ein Gewicht an einer Feder und und pendelt auf und ab. Dafür kann man die oben stehende Formel benutzen, wobei D die Federkonstante ist.
Ein weiteres Beispiel für eine harmonische Schwingung ist das Fadenpendels, wobei ein Gewicht an einem Faden hängt und es hin und her Schwingt. Hierbei kommt nun die Zentripetalkraft ins Spiel. Mit Hilfe dieser und der Gewichtskraft kann man die Formel für die Kraft der Auslenkung aufstellen
Setzt man diese mit der Kraftgleichung einer harmonischen Schwingung gleich, erhält man diese Gleichung
Setz man diese nun in die Gleichung zur Schwingungsdauer ein erhält man abschließend die Gleichung eines Fandenpendels.
Metzler: S.110; Tafelwerk: S.114