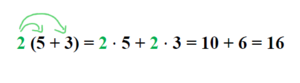Jule Volbers/Testseite: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 5: | Zeile 5: | ||
Kaum tauchen Buchstaben auf, wird Mathe für manche kompliziert. Dabei sind '''Variablen, Terme und Gleichungen''' sehr nützliche ud häufig benötigte Werkzeuge, die man sicher nutzen können sollte. In diesem Kapitel geht es darum, grundlegende Begriffe und Verfahren zum Aufstellen und Umformen von Termen sowie dem Lösen von Gleichungen zu wiederholen. Im Anschluss findest kannst du dein Wissen in Anwendungsaufgaben testen. <br/> <br/> <br/> | Kaum tauchen Buchstaben auf, wird Mathe für manche kompliziert. Dabei sind '''Variablen, Terme und Gleichungen''' sehr nützliche ud häufig benötigte Werkzeuge, die man sicher nutzen können sollte. In diesem Kapitel geht es darum, grundlegende Begriffe und Verfahren zum Aufstellen und Umformen von Termen sowie dem Lösen von Gleichungen zu wiederholen. Im Anschluss findest kannst du dein Wissen in Anwendungsaufgaben testen. <br/> <br/> <br/> | ||
<br/> | <br/> | ||
Version vom 3. Mai 2023, 08:09 Uhr
Kaum tauchen Buchstaben auf, wird Mathe für manche kompliziert. Dabei sind Variablen, Terme und Gleichungen sehr nützliche ud häufig benötigte Werkzeuge, die man sicher nutzen können sollte. In diesem Kapitel geht es darum, grundlegende Begriffe und Verfahren zum Aufstellen und Umformen von Termen sowie dem Lösen von Gleichungen zu wiederholen. Im Anschluss findest kannst du dein Wissen in Anwendungsaufgaben testen.
Inhaltsverzeichnis
1.Terme, Variable und Gleichungen
Ergänze den Lückentext. Prüfe das Ergebnis und übertrage die Lösung in den Kasten zur Aufgabe in deinem Begleitmaterial.
Variablen sind Zeichen (meistens kleine Buchstaben). Sie sind Platzhalter. Du kannst Zahlen für sie einsetzen. Terme sind Rechenausdrücke. Terme können Zahlen, Rechenzeichen, Klammern und Variablen enthalten. Werden zwei Terme mit einem Gleichheitszeichen verbunden, entsteht eine Gleichung. Es gibt verschiedene Arten von Gleichungen. Bei linearen Gleichungen ist die größte Potenz der Varialbe 1, bei quadratischen Gleichungen 2.
Teste dein Wissen!
2.Terme
Terme aufstellen
Du hast gelernt, Sachsituationen mit Hilfe von Termen zu beschreiben. Hier kannst du dein Wissen testen.
Kreuze auch hier den passenden Term an.
Terme vereinfachen
Um Produktterme so einfach wie möglich zu schreiben, dürfen überflüssige Malpunkte weggelassen werden. Dies sind Malpunkte zwischen einer Zahl und einer Variablen und zwischen einer Zahl oder Variablen und einer Klammer.Markiere die überflüssigen Malpunkte in den Termen.
Vereinfache die Terme soweit wie möglich. Übertrage die Ergebnisse in den Kasten zur Aufgabe in deinem Begleitmaterial. Wenn du dir unsicher bist, schaue dir die Tipps an.
Zusammenfassen von Summen:
a)
b)
c)
d)
e)
f)
Beim Zusammenfassen von Summen gilt:
- Nur gleiche Variablen dürfen zusammengefasst werden.
- Auch die Potenz muss übereinstimmen.
- Die Rechenregeln für das Rechnen mit ganzen Zahlen müssen beachtet werden.
- Es kann helfen, gleiche Summanden farbig zu markieren.
Beispiele:
1)
2)
Zusammenfassen von Produkten
f)
g)
Beim Zusammenfassen von Produkten gilt:
- Es können auch Teile mit unterschiedlichen Potenzen oder Variablen zusammengefasst werden.
- Der Multiplikationspunkt muss nicht notiert werden
= 2a
- Beachte die Vorzeichen der Faktoren!
a) =
b) =
c) =
d) =
e) =
f)
Wichtig: Unterscheide
Denke daran. Es gilt:
ergibt:
ergibt:
ergibt:
ergibt:
Füge die zugehörigen Terme zusammen. Du kannst hierfür deinen Stift und Papier nutzen.
Klammern in Termen
Erkläre mit Hilfe der Abbildung, dass für das Auflösen von Klammern gilt:
.
.
Formuliere die Regel in eigenen Worten. Wende sie auf das Beispiel a = 2, b = 5 und c = 3 an. Kontrolliere dann deine Lösung.
Der Flächeninhalt des blauen Rechtecks ist , der des roten Rechtecks
. Die beiden Rechtecks bilden ein großes Rechteck mit den Seitenlängen
. Der Flächeninhalts dieses Rechtecks kann auf 2 Arten berechnet werden: Agroß =
oder durch Addition der beiden Flächeninhalte der kleinen Rechtecke:
.
Dies ist die Erklärung der ersten Gleichung. Da die Multiplikation kommutativ ist (z.B. ist ab = ba), gilt auch die 2. Gleichung.
Formulierung in eigenen Worten: Durch Man multipliziert einen Faktor mit einer Klammer, indem man den Faktor mit jedem einzelnen Glied in der Klammer multipliziert.
Es spielt keine Rolle, ob der Faktor links oder rechts von der Klammer steht:
Erinnerung
- Achte darauf, ob in der Klammer eine Summe oder Differenz steht, denn:
- Bei Minusklammern, also wenn vor der Klammer ein negativer Faktor steht, drehen sich die Vorzeichen von jedem Glied in der Klammer um:
.
.
b)
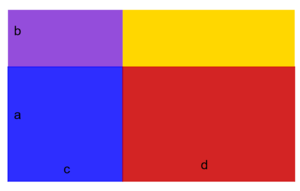
Erkläre mit Hilfe der Abbildung, dass für die Multiplikation zweier Summen oder Differenzen folgende Regel gilt:
. Erkläre die Regel in eigenen Worten und wende sie auf das Beispiel a = 2, b = 3, c = 7 und d = -2 an. Kontrolliere dann deine Lösung
Hier bilden die vier kleinen Rechtecke ein großes Rechteck. Die Flächeninhalte der einzelnen Rechtecke sind:
(blau),
(lila),
(rot),
(gelb).
Auch hier bilden die kleinen Rechtecke ein großes Rechteck mit den Seitenlängen
Der Flächeninhalt des großen Rechtecks lässt sich wieder auf zwei Arten berechnen: Agroß = oder durch Addition der vier Flächeninhalte der kleinen Rechtecke:
.
Formulierung in eigenen Worten: Zwei Summen (oder Differenzen) werden miteinander multipliziert, indem man jeden Summanden der ersten Klammer mit jedem Summanden der zweiten Klammer multipliziert:
Es ist
.
.
.
Ergänze den Lückentext. Prüfe das Ergebnis und übertrage die Lösung in den Kasten "Klammern in Termen" in deinem Begleitheft.
Das Ausmultiplizieren hat zum Ziel, eine Klammer aufzulösen. Man multipliziert einen Faktor mit einer Klammer, indem man den Faktor mit jedem einzelnen Glied in der Klammer multipliziert.
.
Diese Regel nennt man Distributivgesetz.
Es spielt keine Rolle, ob der Faktor links oder rechts von der Klammer steht:
Steht ein negativer Faktor vor der Klammer, drehen sich die Vorzeichen beim Auflösen der Klammer herum:
- a(b - c) = - ab + ac.
Zwei Summen (oder Differenzen) werden miteinander multipliziert, indem man jeden Summanden der ersten Klammer mit jedem Summanden der zweiten Klammer multipliziert:
.
In dieser Aufgabe kannst du das Ausmultiplizieren üben. Ordne jedem Klammerterm die richtige ausmultiplizierte Lösung zu. Nimm dir einen Zettel für Nebenrechnungen zur Hilfe.
a)
b)
c)
d)
d)
f)
Jetzt geht es um den umgekehrten Weg. Beim Ausklammern wird eine Summe in ein Produkt umgewandelt, es werden also Klammern hinzugefügt.
Dies ist nur dann möglich, wenn die Summanden gemeinsame Faktoren haben.
Suche in den LearningApps nach gemeinsamen Faktoren der Summanden und klammere diese dann aus. Achtung: Du musst alle gemeinsamen Faktoren ausklammern. Wenn du dir unsicher bist, schaue dir zuerst das Beispiel an. Übertrage die Ergebnisse nach der Kontrolle in den Kasten zur Aufgabe in deinem Begleitheft.
8x + 12xy
= 4x⋅2 + 4x⋅3y
3. Gleichungen
Lineare und quadratische Gleichungen. Eine lineare Gleichung ist eine Gleichung 1. Grades. Das heißt: Die Variable x hat als Exponenten höchstens die Zahl 1:
.
Ihre einfachste Form ist:
, wobei
und
reelle Zahlen sind
und
eine Variable.
Eine quadratische Gleichung ist eine Gleichung 2. Grades. Das heißt: Die Variable x hat als Exponenten höchstens die Zahl 2. Zum Beispiel:
oder
. Die Verfahren zur Lösung solcher Gleichungen sollst du jetzt wiederholen.
Das Verfahren zum Lösen linearer Gleichungen hast du bereits kennengelernt. Die folgende Learning-App hilft dir, dich zu erinnern.
Vorgehensweise zum Lösen von Gleichungen Bringe die Schritte in die richtige Reihenfolge, übertrage diese dann in den Kasten zur Aufgabe in deinem Begleitheft.
- Löse die Klammern auf.
- Fasse die Terme auf beiden Seiten zusammen.
- Bringe die Summanden mit Variablen und die Summanden ohne Variablen jeweils auf eine Seite, fasse sie zusammen bzw. ordne sie.
- Dividiere durch den Faktor vor der Variable.
Beispiel:

Löse die Gleichungen. Führe, wenn möglich, eine Probe durch. Denke daran: Eine Probe kann nur durchgeführt werden, wenn es mindestens eine Lösung für die Gleichung gibt.
a)
Probe:
b)
Probe:
c)
d)
Probe:
e)
Ein Produkt ist dann , wenn einer der Faktoren
ist. Deshalb kann man die Aufgabe so lösen:
Probe:
f)
Probe:
Löse die quadratischen Gleichungen ohne p-q-Formel. Nutze hierfür den Kasten zur Aufgabe in deinem Begleitmaterial. Kontrolliere deine Lösung.
a)
b)
c)
d)
e)
zu a)
zu b)
keine Lösung (in den reellen Zahlen)
zu c)
zu d)
zu e)
Löse die quadratischen Gleichungen. Nutze hierfür den Kasten zur Aufgabe in deinem Begleitmaterial. Kontrolliere deine Lösung.
a)
b)
c)
zu a)
zu b)
zu c)
4. Aufgaben zum Trainieren
Wenn man zur Zahl das Doppelte einer Zahl addiert, so erhält man das Vierfache der gesuchten Zahl. Stelle eine geeignete Gleichung auf und ermittle die gesuchte Zahl (Extrablatt). Trage die geforderten Angaben in den Kasten zur Aufgabe in deinem Begleitheft ein.
Das Doppelte einer Zahl:
Zur Zahl das Doppelte einer Zahl addieren:
. Dies wird die linke Seite der Gleichung bilden.
Das Vierfache der gesuchten Zahl: . Dies ist die rechte Seite der Gleichung.
Wir erhalten also die Gleichung:
.
Um das gesuchte zu finden, lösen wir die Gleichung, indem wir sie nach
umstellen. Achte darauf alle Umformungen immer auf beiden Seiten der Gleichung durchzuführen.
Die gesuchte Zahl ist .
Probe:
Die Mutter von Leon ist -mal so alt wie er. In
Jahren wird sie doppelt so alt sein wie Leon. Ermittle, wie alt Leon und seine Mutter heute sind (Extrablatt). Trage die geforderten Angaben in den Kasten zur Aufgabe in deinem Begleitheft ein.
Bezeichne mit das Alter der Mutter und mit
das Alter von Leon.
Die erste Gleichung ist
,da die Mutter von Leon 3-mal so alt ist wie er.
Außerdem gilt die zweite Gleichung
. Die linke Seite der Gleichung beschreibt das Alter der Mutter in 12 Jahren. Dies entspricht der rechten Seite der Gleichung, da das Alter der Mutter in 12 Jahren dann das doppelte des Alters von Leon in 12 Jahren beträgt.
Setze nun in die zweite Gleichung ein:
Leon ist heute also 12 Jahre alt.
Um das Alter der Mutter zu bestimmen, setzten wir in die erste Gleichung ein:
Die Mutter ist heute also 36 Jahre alt.
Probe erste Gleichung:
Probe zweite Gleichung:
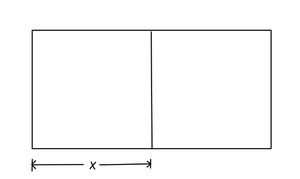
Klicke alle Terme an, die den Flächeninhalt der Fläche beschreiben.
Wir erhalten die Gleichung: , da insgesamt
Meter Seil zur Verfügung stehen und drei Meter Seil für die Abspannung an den Pfosten benötigt werden.
Diese Gleichung können wir lösen:
Probe:
Landwirt Mertens hat bisher eine quadratische Weide für seine paar Schafe. Da nun an dieser Stelle eine Landstraße ausgebaut werden soll, fragt die Stadt den Landwirt, ob er ein flächengleiches, rechteckiges Grundstück auf der anderen Seite seines Bauernhofes gegen seine quadratische Weide tauschen würde. Diese Weide ist zwar vier Meter kürzer, dafür aber sechs Meter länger.
Landwirt Mertens überlegt:
- Hilf ihm und finde die Maße (Seitenlängen und Flächeninhalte) der Weiden heraus. Nutze zur Rechnung ein Extrablatt. Trage die geforderten Angaben in den Kasten zur Aufgabe in deinem Begleitheft ein. Wenn du nicht weißt, wie du vorgehen sollst, schaue dir nach und nach die Tipps unten an.
Was ist gegeben?
zwei flächengleiche Flächen (Quadrat und Rechteck). Wähle die Variable x = Seitenlänge der quadratischen Fläche
x = Seitenlänge der quadratischen WeideDie beiden Weiden sind flächengleich, d.h. ihr Flächeninhalt ist gleich.
Benutze zum Aufstellen der Gleichung die Formeln für die Berechnung des Flächeninhaltes eines Quadrats und eines Rechtecks.
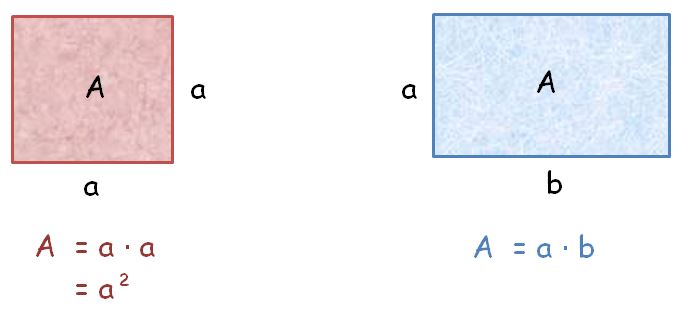
Beide Flächen sind gleich groß, daher lautet die Gleichung:
x² = (x – 4) (x + 6)
Versuche nun x zu berechnen. Löse hierfür zunächst die Klammern auf.Die korrekte Gleichung lautet: x² = (x-4)(x+6).
Du hast nun herausgefunden, dass die Länge und Breite der quadratischen Weide je 12m beträgt. Damit kannst du jetzt die Seitenlängen der rechteckigen Weide berechnen.
- 12 - 4 = 8 (eine Seitenlänge des Rechtecks)
- 12 + 6 = 18 (andere Seitenlänge des Rechtecks)
Beide Weiden haben einen Flächeninhalt von 144 m²
Die Katheten eines rechtwinkligen Dreieckes unterscheiden sich um 1 cm. Wie lang sind die Katheten, wenn die Hypotenuse 5 cm lang ist? Nutze zur Lösung ein Extrablatt. Trage die geforderten Angaben in den Kasten zur Aufgabe in deinem Begleitheft ein. Nutze die Tipps, wenn du nicht weiterweißt.
x: Länge der kürzeren Kathete. Dann ist (x+1) die Länge der längeren Kathete.
Nach dem Satz des Pythagoras gilt: