Benutzer:Meike WWU-12/Entwurf des Lernpfadkapitels: Unfallforensiker*in: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 132: | Zeile 132: | ||
|3=Kurzinfo}} | |3=Kurzinfo}} | ||
{{Box | 1=Merksatz: Formel für die kinetische Energie | 2=Die kinetische Energie bestimmt man mit der Formel <math>E = \frac{m | {{Box | 1=Merksatz: Formel für die kinetische Energie | 2=Die kinetische Energie bestimmt man mit der Formel <math>E = \frac{m \cdot v^2}{2}</math>.| 3=Merksatz |Farbe={{Farbe|grün|dunkel}}}} | ||
Das Auto im Unfall aus Aufgabe 2a wiegt ca. 1,4 t. Bestimme die kinetische Energie beim Aufprall, wenn davon ausgegangen wird, dass nicht gebremst wurde. | Das Auto im Unfall aus Aufgabe 2a wiegt ca. <math>1,4</math> t. Bestimme die kinetische Energie beim Aufprall, wenn davon ausgegangen wird, dass nicht gebremst wurde. | ||
| Arbeitsmethode | Farbe=#CD2990 }} | | Arbeitsmethode | Farbe=#CD2990 }} | ||
| Zeile 145: | Zeile 145: | ||
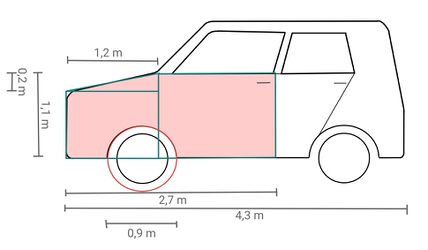
'''Ordne den verschiedenen geometrischen Formen die passende Skizze sowie die geeignete Formel zur Berechnung des Flächeninhalts A zu. Überprüfe deine Lösung.''' | '''Ordne den verschiedenen geometrischen Formen die passende Skizze sowie die geeignete Formel zur Berechnung des Flächeninhalts <math>A</math> zu. Überprüfe deine Lösung.''' | ||
{{LearningApp|width=100%|height=500px|app=pnf5uwamn23}} | {{LearningApp|width=100%|height=500px|app=pnf5uwamn23}} | ||
| Zeile 168: | Zeile 168: | ||
Anschließend werden die Teilflächen addiert (die grün umrandeten Flächen) bzw. die halbe Reifenfläche (Hälfte des rot umrundeten Kreis) wird abgezogen,|2=Tipp|3=Tipp verbergen}} | Anschließend werden die Teilflächen addiert (die grün umrandeten Flächen) bzw. die halbe Reifenfläche (Hälfte des rot umrundeten Kreis) wird abgezogen,|2=Tipp|3=Tipp verbergen}} | ||
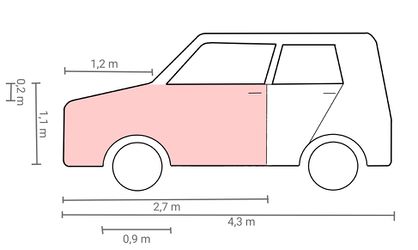
{{Lösung versteckt|1= Je nachdem, wie du die Fläche eingeteilt hast, kann deine Lösung etwas von dieser abweichen. Nach dieser Näherungslösung ist die beschädigte Fläche ca. 1,58 m<sup>2</sup> groß.|2=Lösung|3=Lösung verbergen}} | {{Lösung versteckt|1= Je nachdem, wie du die Fläche eingeteilt hast, kann deine Lösung etwas von dieser abweichen. Nach dieser Näherungslösung ist die beschädigte Fläche ca. <math>1,58</math> m<sup>2</sup> groß.|2=Lösung|3=Lösung verbergen}} | ||
|Arbeitsmethode | Farbe={{Farbe|orange}} }} | |Arbeitsmethode | Farbe={{Farbe|orange}} }} | ||
{{Box | Aufgabe 2d⭐: Schadensbegutachtung | | {{Box | Aufgabe 2d⭐: Schadensbegutachtung | | ||
Nach Absprache mit einer Werkstatt erfährst du, dass die Reparaturkosten 2.500 € betragen. Das Auto hat ursprünglich 21.000 € gekostet und hatte durch den alltäglichen Verschleiß und das Alter vor dem Unfall bereits einen Werteverlust von 30%. | Nach Absprache mit einer Werkstatt erfährst du, dass die Reparaturkosten <math>2.500</math> € betragen. Das Auto hat ursprünglich <math>21.000</math> € gekostet und hatte durch den alltäglichen Verschleiß und das Alter vor dem Unfall bereits einen Werteverlust von 30%. | ||
{{Box | {{Box | ||
| Zeile 184: | Zeile 184: | ||
{{LearningApp|width=100%|height=500px|app=pgqvqcz9j23}} | {{LearningApp|width=100%|height=500px|app=pgqvqcz9j23}} | ||
{{Lösung versteckt|1=Zur Berechnung des Wertes vor dem Unfall benötigst du Prozentrechnung. Dabei gilt allgemein | {{Lösung versteckt|1=Zur Berechnung des Wertes vor dem Unfall benötigst du Prozentrechnung. Dabei gilt allgemein <math>W=p \cdot G</math>, wobei <math>W</math> der '''Prozentwert''', <math>p</math> der '''Prozentsatz''' und <math>G</math> der '''Grundwert''' ist. | ||
Zur Berechnung des Autowertes vor dem Unfall kannst du also die Werte (Neupreis und 100%-30%=70%) einsetzen, der Prozentsatz muss dabei geändert werden, da nicht der Wertverlust, sondern der Restwert berechnet werden soll. | Zur Berechnung des Autowertes vor dem Unfall kannst du also die Werte (Neupreis und <math>100 \text{%} - 30 \text{%} = 70 \text{%}</math>) einsetzen, der Prozentsatz muss dabei geändert werden, da nicht der Wertverlust, sondern der Restwert berechnet werden soll. | ||
Um dann den Anteil der Reparaturkosten an diesem Wert, also den Prozentsatz, auszurechnen, solltest du zusätzlich noch in einer Äquivalenzumformung die Formel umstellen.|2=Tipp|3=Tipp verbergen}} | Um dann den Anteil der Reparaturkosten an diesem Wert, also den Prozentsatz, auszurechnen, solltest du zusätzlich noch in einer Äquivalenzumformung die Formel umstellen.|2=Tipp|3=Tipp verbergen}} | ||
| Zeile 193: | Zeile 193: | ||
Zu dem '''Restwert''' vor dem Unfall: | Zu dem '''Restwert''' vor dem Unfall: | ||
Es gilt p=70%=0,7, da der Restwert und nicht der Verlust berechnet werden soll, und G=21000 [€]. | Es gilt <math>p=70 \text{%} =0,7</math>, da der Restwert und nicht der Verlust berechnet werden soll, und <math>G=21000</math> [€]. | ||
Somit W=14700 [€] | Somit <math>W=14700</math> [€] | ||
Zum '''Prozentsatz''' der Reparaturkosten am Restwert: | Zum '''Prozentsatz''' der Reparaturkosten am Restwert: | ||
| Zeile 200: | Zeile 200: | ||
W &=p*G \Leftrightarrow p &=\tfrac{W}{G} | W &=p*G \Leftrightarrow p &=\tfrac{W}{G} | ||
\end{align}</math> | \end{align}</math> | ||
Da der Prozentsatz der Raperaturkosten am Restwert berechnet werden soll, ist der neue Grundwert allerdings G=14700 und der Prozentwert ist W=2500. | Da der Prozentsatz der Raperaturkosten am Restwert berechnet werden soll, ist der neue Grundwert allerdings <math>G=14700</math> und der Prozentwert ist <math>W=2500</math>. | ||
Somit gilt p≈0,17=17%. | Somit gilt <math>p≈0,17=17 \text{%}</math>. | ||
Der Prozentsart der Reparaturkosten am Restwert des Autos beträgt also ca. 17%. | Der Prozentsart der Reparaturkosten am Restwert des Autos beträgt also ca. <math>17 /text{%}</math>. | ||
|2=Lösungsweg|3=Lösungsweg verbergen}} | |2=Lösungsweg|3=Lösungsweg verbergen}} | ||
| Arbeitsmethode}} | | Arbeitsmethode}} | ||
| Zeile 215: | Zeile 215: | ||
{{Box | {{Box | ||
|1=Info | |1=Info | ||
|2=Die Länge des Bremsweges b in m bestimmt man mit der Formel b(x)=x^2/ | |2=Die Länge des Bremsweges <math>b</math> in m bestimmt man mit der Formel <math>b(x) = \frac{x^2}{100}</math>, wobei <math>x</math> für die Geschwindigkeit in km/h steht. | ||
|3=Kurzinfo}} | |3=Kurzinfo}} | ||
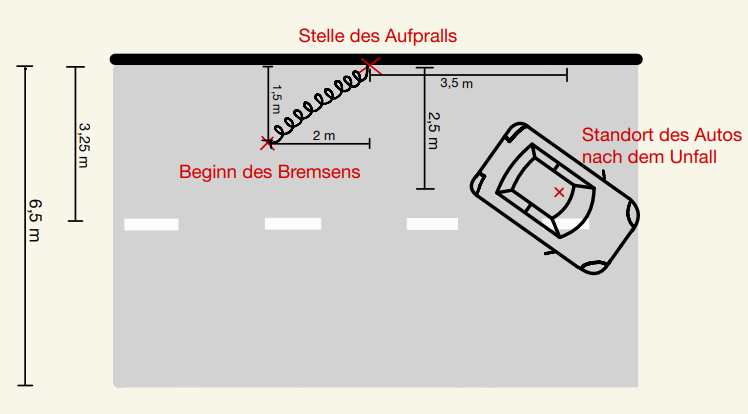
Bei dem Unfall ist eine Bremsspur mit einer Länge von | Bei dem Unfall ist eine Bremsspur mit einer Länge von <math>49</math> m entstanden. Berechne, wie hoch die Geschwindigkeit vor dem Unfall war. | ||
Hat sich die fahrende Person an die vorgeschriebene Geschwindigkeit von | Hat sich die fahrende Person an die vorgeschriebene Geschwindigkeit von <math>50</math> km/h gehalten? | ||
{{Lösung versteckt|1=Nutze Äquivalenzumformungen! Wir wissen, dass der Bremsweg | {{Lösung versteckt|1=Nutze Äquivalenzumformungen! Wir wissen, dass der Bremsweg <math>49</math> m betrug. Löse die Gleichung <math>49 = \frac{x^2}{100}</math> nach <math>x</math> auf, um die Geschwindigkeit zu bestimmen.|2=Tipp 1|3=Tipp 1 verbergen}} | ||
{{Lösung versteckt|1=Multipliziere zunächst beide Seiten der Gleichung mit 100.|2=Tipp 2|3=Tipp 2 verbergen}} | {{Lösung versteckt|1=Multipliziere zunächst beide Seiten der Gleichung mit <math>100</math>.|2=Tipp 2|3=Tipp 2 verbergen}} | ||
{{Lösung versteckt|1=Ziehe schließlich auf beiden Seiten der Gleichung die Wurzel.|2=Tipp 3|3=Tipp 3 verbergen}} | {{Lösung versteckt|1=Ziehe schließlich auf beiden Seiten der Gleichung die Wurzel.|2=Tipp 3|3=Tipp 3 verbergen}} | ||
| Arbeitsmethode}} | | Arbeitsmethode}} | ||
Version vom 22. April 2023, 16:41 Uhr
Unfallforensiker:in
Aufgabe 1: Unfallrekonstruktion
Aufgabe 2: Unfallgutachten