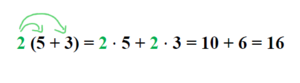Jule Volbers/Testseite: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 325: | Zeile 325: | ||
{{Lösung versteckt|1=zu a und b): Bei Gleichungen der Form <math>ax^2+c</math>, also ohne linearen Summanden <math>bx</math> kannst du die Gleichung umstellen, sodass <math>x^2</math> alleine steht und anschließend - falls möglich - die Wurzel ziehen.|2=Tipp 1|3=schließen}} | {{Lösung versteckt|1=zu a und b): Bei Gleichungen der Form <math>ax^2+c</math>, also ohne linearen Summanden <math>bx</math> kannst du die Gleichung umstellen, sodass <math>x^2</math> alleine steht und anschließend - falls möglich - die Wurzel ziehen.|2=Tipp 1|3=schließen}} | ||
{{Lösung versteckt|1=zu a): Achte beim Wurzelziehen auf die positive und negative Lösung.|2=Tipp 2|3=schließen}} | {{Lösung versteckt|1=zu a): Achte beim Wurzelziehen auf die positive und negative Lösung.|2=Tipp 2|3=schließen}} | ||
{{Lösung versteckt|1=zu b): Erinnere dich: Wann kannst du aus einer Zahl die Wurzel ziehen? |2=Tipp | {{Lösung versteckt|1=zu b): Erinnere dich: Wann kannst du aus einer Zahl die Wurzel ziehen? |2=Tipp 3|3=schließen}} | ||
{{Lösung versteckt|1=zu c): Bei Gleichungen der Form <math>ax^2+bx</math>, also ohne konstanten Summanden <math>c</math> kannst du <math>x</math> ausklammern.|2=Tipp | {{Lösung versteckt|1=zu c): Bei Gleichungen der Form <math>ax^2+bx</math>, also ohne konstanten Summanden <math>c</math> kannst du <math>x</math> ausklammern.|2=Tipp 4|3=schließen}} | ||
{{Lösung versteckt|1=zu c): Ein Produkt ist genau dann <math>0</math>, wenn einer der beiden Faktoren bereits <math>0</math> ist. ''Beispiel:'' <math>{\color{blue}x} \cdot ({\color{red}x-2})=0</math> bedeutet, dass entweder <math>{\color{blue}x}=0</math> oder <math>{\color{red}x-2}=0</math> gilt.|2=Tipp | {{Lösung versteckt|1=zu c): Ein Produkt ist genau dann <math>0</math>, wenn einer der beiden Faktoren bereits <math>0</math> ist. ''Beispiel:'' <math>{\color{blue}x} \cdot ({\color{red}x-2})=0</math> bedeutet, dass entweder <math>{\color{blue}x}=0</math> oder <math>{\color{red}x-2}=0</math> gilt.|2=Tipp 5|3=schließen}} | ||
{{Lösung versteckt|1=zu d): Stelle um, sodass auf einer Seite des Gleichheitszeichen <math>0</math> steht.|2=Tipp | {{Lösung versteckt|1=zu d): Stelle um, sodass auf einer Seite des Gleichheitszeichen <math>0</math> steht.|2=Tipp 6|3=schließen}} | ||
{{Lösung versteckt|1=zu e): Ziehe zunächst auf beiden Seiten die Wurzel. Achte auf die positive und negative Lösung. |2=Tipp | {{Lösung versteckt|1=zu e): Ziehe zunächst auf beiden Seiten die Wurzel. Achte auf die positive und negative Lösung. |2=Tipp 7|3=schließen}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
| Zeile 346: | Zeile 346: | ||
\begin{alignat}{3} | \begin{alignat}{3} | ||
& & 0 &= x^2+25 \qquad &&| -25\\ | & & 0 &= x^2+25 \qquad &&| -25\\ | ||
&\Leftrightarrow \qquad & - &= x^2 && | &\Leftrightarrow \qquad & - &= x^2 && \qquad &&| \\ | ||
\end{alignat} | \end{alignat} | ||
</math> | </math> | ||
keine Lösung (in den reellen Zahlen) | |||
zu b) | zu b) | ||
<math> | <math> | ||
Version vom 22. März 2023, 14:21 Uhr
Kaum tauchen Buchstaben auf, wird Mathe für manche kompliziert. Dabei sind Variablen, Terme und Gleichungen sehr nützliche ud häufig benötigte Werkzeuge, die man sicher nutzen können sollte. In diesem Kapitel geht es darum, grundlegende Begriffe und Verfahren zum Aufstellen und Umformen von Termen sowie dem Lösen von Gleichungen zu wiederholen. Im Anschluss findest kannst du dein Wissen in Anwendungsaufgaben testen.
.
1.Terme, Variablen und Gleichungen
2.Terme
Terme aufstellen
Terme vereinfachen
a) =
b) =
c) =
d) =
e) =
f)
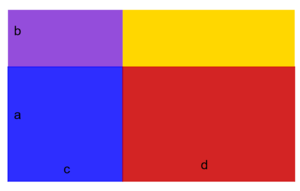
Klammern in Termen
3. Gleichungen
4. Aufgaben zum Trainieren
Zahlenrätsel
Geometrische Anwendungen
Was ist gegeben?
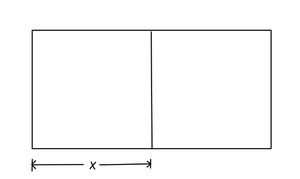
zwei flächengleiche Flächen (Quadrat und Rechteck)
x = Seitenlänge der quadratischen Weide
x - 4 = eine Seitenlänge der rechteckigen Weide (3m kürzer)
x + 6 = andere Seitenlänge der rechteckigen Weide (5m länger)
Die beiden Weiden sind flächengleich, d.h. ihr Flächeninhalt ist gleich.
Benutze zum Aufstellen der Gleichung die Formeln für die Berechnung des Flächeninhaltes eines Quadrats und eines Rechtecks.
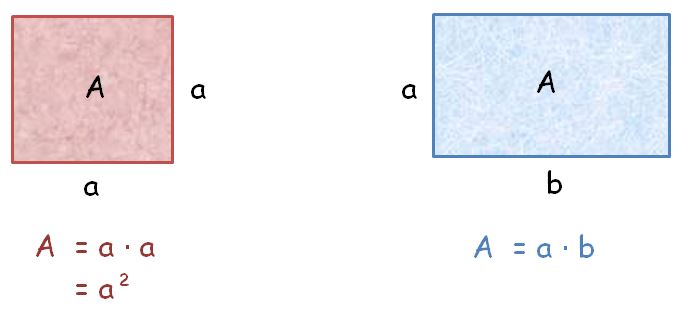
Beide Flächen sind gleich groß, daher lautet die Gleichung:
x² = (x – 4) (x + 6)
Versuche nun x zu berechnen. Löse hierfür zunächst die Klammern auf.Du hast nun herausgefunden, dass die Länge und Breite der quadratischen Weide je 12m beträgt. Damit kannst du jetzt die Seitenlängen der rechteckigen Weide berechnen. Setze hierfür x = 12 in deine aufgestellten Terme ein:
- x - 4 (eine Seitenlänge des Rechtecks)
- x + 6 (andere Seitenlänge des Rechtecks)