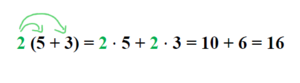Jule Volbers/Testseite

Willkommen auf dem Lernpfad: Nützliche Werkzeuge - Terme und Gleichungen.

In diesem Lernpfad geht es um das Vertiefen deines Wissens über Terme, Variablen und Gleichungen. Du findest hier eine Wiederholung zu den Begriffen und Übungsaufgaben zu den Themen Terme aufstellen, Terme umformen und Gleichungen lösen. .

1.Terme, Variablen und Gleichungen

Was ist Was?" - Wiederhole die Begriffe!

Ergänze den Lückentext. Prüfe das Ergebnis und übertrage die Lösung in den Kasten zur Aufgabe in deinem Begleitmaterial.

Variablen sind Zeichen (meistens kleine Buchstaben). Sie sind Platzhalter. Du kannst Zahlen für sie einsetzen. Terme sind Rechenausdrücke. Terme können Zahlen, Rechenzeichen, Klammern und Variable enthalten. Werden zwei Terme mit einem Gleichheitszeichen verbunden, entsteht eine Gleichung. Es gibt verschiedene Arten von Gleichungen. Wichtige Arten sind die linearen und die quadratischen Gleichungen.

Begriffstraining

Teste dein Wissen!

 

2.Terme

Terme aufstellen

Terme in Sachsituationen

Du hast gelernt, Sachsituationen mit Hilfe von Termen zu beschreiben. Hier kannst du dein Wissen testen.

a)

b)

Terme vereinfachen

Info

Terme enthalten unterschiedliche Rechenoperationen wie Addition, Subtraktion, Multiplikation und Division. Manche Teile von Termen kann man zusammenfassen, um so den Term zu vereinfachen. Du hast die Regeln im Unterricht bereits kennengelernt.

Erinnerung: Überflüssige Malpunkte

Um Produktterme so einfach wie möglich zu schreiben, dürfen überflüssige Malpunkte weggelassen werden. Dies sind Malpunkte zwischen einer Zahl und einer Variablen und zwischen einer Zahl oder Variablen und einer Klammer.Markiere die überflüssigen Malpunkte in den Termen.

Info

Überflüssige Malpunkte werden nicht notiert.

Terme zusammenfassen

Vereinfache die Terme soweit wie möglich. Übertrage die Ergebnisse in den Kasten zur Aufgabe in deinem Begleitmateria. Wenn du dir unsicher bist, schaue dir die Tipps an.
Zusammenfassen von Summen:
a) $2a+10a+11+7$
b) $-4x+5+9x-7$
c) $3a+5a +7b-2b$
d) $-2c+15-4d-3c-5$
e) $13x^2+3x+9y-3y$
f) $2x+xy-3y-2xy+2xy^2$

Beim Zusammenfassen von Summen gilt:

• Nur gleiche Variablen dürfen zusammengefasst werden.
• Auch die Potenz muss übereinstimmen.
• Die Rechenregeln für das Rechnen mit ganzen Zahlen müssen beachtet werden.
• Es kann helfen, gleiche Summanden farbig zu markieren.

Beispiele:
1) ${\color{blue}b}{\color{red}+a+3a}$ $= {\color{blue}b}{\color{red}+4a}$

2) ${\color{orange}2x}{\color{red}+xy}{\color{blue}-3y}{\color{red}-2xy}{\color{green}+2xy^2}$ $= {\color{orange}2x}{\color{blue}-3y}{\color{green}+2xy^2}{\color{red}+xy-2xy}$ $= {\color{orange}2x}{\color{blue}-3y^2}{\color{green}+2xy^2}{\color{red}-xy}$

Hier konnten nur die beiden Teile mit ${\color{red}xy}$ zusammengefasst werden, da alle anderen Variablen unterschiedlich sind bzw. in einer anderen Potenz vorkommen.

Zusammenfassen von Produkten
f) $5{r} 4{r}{s}$
g) $2{x}(-7{x^2y})(-3{y^3})$

Beim Zusammenfassen von Produkten gilt:

• Es können auch Teile mit unterschiedlichen Potenzen oder Variablen zusammengefasst werden.
  
• Der Multiplikationspunkt muss nicht notiert werden ${2}\cdot {a}$ = 2a
  
• Beachte die Vorzeichen der Faktoren!

a) $2a+10b+11+7$ = $12a+18$
b) $-4x+5+9x-7$= $5x-2$
c) $3a+5a+7b-2b$ = $8a+5b$
d) $-2c+15-4d-3c-5$= $-5c-4d+10$
e) $13x^2+3x^2+9y-3y$= $13x^2+3x^2+9y-3y$
f) $5{r}4{r}{s}$ $= 5 \cdot 4 {x} {x} {y}$ $= 20 {x^2}{y}$

g) $2{x}(-7{x^2y})(-3{y^3})$ $= 2 \cdot (-7) \cdot (-3) {x} {x^2} {y} {y^3}$ $= 42{x^3}{y^4}$

Idee

Wichtig: Unterscheide
$(-x) + (-x) = -2x$
$(-x) \cdot (-y) = x \cdot y$

Denke daran. Es gilt:
$+ \cdot +$ ergibt: $+$
$- \cdot -$ ergibt: $+$
$- \cdot +$ ergibt: $-$
$+ \cdot -$ ergibt: $-$

Beachte außerdem die Vorfahrtsregeln: Potenz- vor - Punkt- vor Strichrechnung, die Klammer geht immer vor.

Termtraining.

Füge die zugehörigen Terme zusammen. Du kannst hierfür deinen Stift und Papier nutzen.

 

Klammern in Termen

Klammern auflösen: Das Ausmultiplizieren hat zum Ziel, eine Klammer aufzulösen.

Auflösen von Klammern

Erkläre mit Hilfe der Abbildung, dass für das Auflösen von Klammern gilt:

${\color{green}a}(b+c) = {\color{green}a}b + {\color{green}a}c$.

$(b+c){\color{green}a} = b{\color{green}a} + {\color{green}a}$.

Formuliere die Regel in eigenen Worten. Wende sie auf das Beispiel a = 2, b  = 5 und c = 3 an. Kontrolliere dann deine Lösung.

Man multipliziert einen Faktor mit einer Klammer, indem man den Faktor mit jedem einzelnen Glied in der Klammer multipliziert.

thumb

Es spielt keine Rolle, ob der Faktor links oder rechts von der Klammer steht:

$(5+3) \cdot {\color{green}2} = 5 \cdot {\color{green}2} + 3\cdot {\color{green}2} = 10 + 6 = 16$.

Erinnerung

1. Achte darauf, ob in der Klammer eine Summe oder Differenz steht, denn: $a(b{\color{red}-}c) = a \cdot b {\color{red}-} a\cdot c$

1. Bei Minusklammern, also wenn vor der Klammer ein negativer Faktor steht, drehen sich die Vorzeichen von jedem Glied in der Klammer um:

${\color{red}-}a(b{\color{red}+}c) = {\color{red}-}ab {\color{red}-} ac$.

${\color{red}-}a({\color{red}-}b{\color{red}+}c) = ab {\color{red}-} ac$.

b)

Erkläre mit Hilfe der Abbildung, dass für die Multiplikation zweier Summen oder Differenzen folgende Regel gilt:

$(a+b) (c+d) = ac + ad + bc + bd$. Erkläre die Regel in eigenen Worten und wende sie auf das Beispiel a = 2, b = 3, c = 7 und d = -2 an. Kontrolliere dann deine Lösung

Zwei Summen (oder Differenzen) werden miteinander multipliziert, indem man jeden Summanden der ersten Klammer mit jedem Summanden der zweiten Klammer multipliziert:

Es ist (2+3) (7-2) = 5 \cdot 5 = 25 (2+3)(7-2) = 2 \cdot 7 - 2 \cdot 2 + 3 \cdot 7 - 3 \cdot 2 = 14 - 4 + 21 - 6 = 25

${\color{green}x} (3 + 2) = 3{\color{green}x} + 2{\color{green}x} = 5{\color{green}x}$. ${\color{green}2}(3x - 1) = {\color{green}2} \cdot 3x - {\color{green}2} \cdot 1 = 6x - 2$. ${\color{red}-}(a{\color{red}+}b) = {\color{red}-}a {\color{red}-} b$.

${\color{red}-}(a{\color{red}-}b) = {\color{red}-}a {\color{red}+} b$.

Merke: Auflösen von Klammern

Ergänze den Lückentext. Prüfe das Ergebnis und übertrage die Lösung in den Kasten "Klammern in Termen" in deinem Begleitheft.

Das Ausmultiplizieren hat zum Ziel, eine Klammer aufzulösen. Man multipliziert einen Faktor mit einer Klammer, indem man den Faktor mit jedem einzelnen Glied in der Klammer multipliziert.
${\color{green}a}(b+c) = {\color{green}a}b + {\color{green}a}c$. Diese Regel nennt man Distributivgesetz.
Es spielt keine Rolle, ob der Faktor links oder rechts von der Klammer steht:
$(b+c) {\color{green}a} = b{\color{green}a} + c{\color{green}a} = {\color{green}a}b + {\color{green}a}c = {\color{green}a}(b+c)$
Steht ein negativer Faktor vor der Klammer, drehen sich die Vorzeichen beim Auflösen der Klammer herum: - a(b - c) = - ab + ac. Zwei Summen (oder Differenzen) werden miteinander multipliziert, indem man jeden Summanden der ersten Klammer mit jedem Summanden der zweiten Klammer multipliziert: $(a+b)(c+d) = ac + ad + bc + bd$.

Training zum Ausmultiplizieren

In dieser Aufgabe kannst du das Ausmultiplizieren üben. Ordne jedem Klammerterm die richtige ausmultiplizierte Lösung zu. Nimm dir einen Zettel für Nebenrechnungen zur Hilfe.

a) $(5b+c+3d)\cdot a =$ $5ab+ac+3ad$
b) $(5a+4b)\cdot 4 =$ $16b+20a$
c) $-8(a-2b) =$ $16b-8a$
d) $(2x+5)(3x-7) =$ $6x^2+x-35$
d) $(5a+10b)(\frac{1}{5}c+2d) =$ $ac+10ad+2bc+20bd$
f) $-\frac{1}{2}(\frac{1}{2}a+\frac{1}{2}b) =$ $-\frac{1}{4}a-\frac{1}{4}b$

 

Ausklammern Beim Ausklammern wird eine Summe in ein Produkt umgewandelt, es werden also Klammern hinzugefügt. Dies ist nur dann möglich, wenn die Summanden gemeinsame Faktoren haben.

Ausklammern

Suche in den LearningApps nach gemeinsamen Faktoren der Summenden und klammere diese dann aus. Wenn du dir unsicher bist, schaue dir zuerst das Beispiel an. Übertrage die Ergebnisse nach der Kontrolle in den Kasten zur Aufgabe in deinem Begleitheft.

8x + 12xy
= 4x⋅2 + 4x⋅3y

= 4x⋅(2 + 3y)

3. Gleichungen

Idee

Lineare und quadratische Gleichungen. Eine lineare Gleichung ist eine Gleichung 1. Grades. Das heißt: Die Variable x hat als Exponenten höchstens die Zahl 1: $x^1=x$. Ihre einfachste Form ist: $a x + b = 0$, wobei $a$ und $b$ reelle Zahlen sind und $x$ eine Variable. Eine quadratische Gleichung ist eine Gleichung 2. Grades. Das heißt: Die Variable x hat als Exponenten höchstens die Zahl 2. Zum Beispiel: $x^2 = 9$ oder $2x^2 +5x - 8 = 0$. Die Verfahren zur Lösung solcher Gleichungen sollst du jetzt wiederholen.

Verfahren zum Lösen linearer Gleichungen

Das Verfahren zum Lösen linearer Gleichungen hast du bereits kennengelernt. Die folgende Learning-App hilft dir, dich zu erinnern.

Merke

Vorgehensweise zum Lösen von Gleichungen Bringe die Schritte in die richtige Reihenfolge, übertrage diese dann in den Kasten zur Aufgabe in deinem Begleitheft.

1. Löse die Klammern auf.
2. Fasse die Terme auf beiden Seiten zusammen.
3. Bringe die Summanden mit Variablen und die Summanden ohne Variablen jeweils auf eine Seite, fasse sie zusammen bzw. ordne sie.
4. Dividiere durch den Faktor vor der Variable.

Beispiel:

Training: lineare Gleichungen lösen

Löse die Gleichungen. Führe, wenn möglich, eine Probe durch. Denke daran: Eine Probe kann nur durchgeführt werden, wenn es mindestens eine Lösung für die Gleichung gibt.

a) $2a-64=5+a$

$\begin{align} & & a-64 &=5+a & &\mid +64\\ \Leftrightarrow & & a &=69 \\ \end{align}$

Probe:

$\begin{align} & & 69-64 &=5 \\ \Leftrightarrow & & 69-64 &=5\\ \Leftrightarrow & & 5 &=5 \end{align}$

b) $3x+7=16$

$\begin{align} & & 3x+7&=16 & &\mid -7\\ \Leftrightarrow & & 3x &=9 & &\mid :3\\ \Leftrightarrow & & x &=3\\ \end{align}$

Probe:

$\begin{align} & & 3\cdot 3+7&=16\\ \Leftrightarrow & & 9+7 &=16\\ \Leftrightarrow & & 16 &=16 \end{align}$

c) $4(x+1)-4x-5=1$

$\begin{align} & & 4(x+1)-4x-5 &=1\\ \Leftrightarrow & & 4x+4-4x-5 &=1\\ \Leftrightarrow & & 4x-4x+4-5 &=1\\ \Leftrightarrow & & -1 &=1 \end{align}$

Das ist ein Widerspruch. Deshalb ist die Lösungsmenge leer: $\mathbb{L}=\{\}$. Hier ist keine Probe durch Einsetzen möglich, weil die Lösungsmenge leer ist.

d) $\frac{1}{2x}=0,5$

Versuche die Gleichung so umzustellen, dass du Brüche kürzen kannst.

$\begin{align} & & \frac{1}{2x} &=0,5 & & \mid \cdot 2x\\ \Leftrightarrow & & \frac{1}{2x} \cdot 2x &= 0,5 \cdot 2x & & \mid \text{kürzen}\\ \Leftrightarrow & & 1 &=0,5\cdot 2x & & \mid :0,5\\ \Leftrightarrow & & \frac{1}{0,5} &=\frac{0,5}{0,5} \cdot 2x & & \mid \text{kürzen}\\ \Leftrightarrow & & 2 &=2x & &\mid :2\\ \Leftrightarrow & & 1 &=x\\ & & \mathbb{L}=\{1\} \end{align}$

Probe:

$\begin{align} & & \frac{1}{2 \cdot 1} &=0,5 & &\\ \Leftrightarrow & & \frac{1}{2} &=0,5 & &\\ \Leftrightarrow & & 0,5 &=0,5 \end{align}$

e) $d\cdot (d-5)=0$

Überlege dir, was für zwei Faktoren gilt, deren Produkt $0$ ist.

Ein Produkt ist dann $0$, wenn einer der Faktoren $0$ ist. Deshalb kann man die Aufgabe so lösen:

$\begin{align} & & d\cdot (d-5)&=0\\ \Leftrightarrow & & d=0 &\text{ oder } d-5=0\\ \Leftrightarrow & & d=0 &\text{ oder } d=5\\ & & \mathbb{L}=\{0,5\} \end{align}$

Probe:

$\begin{align} & & 0\cdot (0-5)&=0\\ \Leftrightarrow & & 0&=0 \end{align}$

$\begin{align} & & 5\cdot (5-5)&=0\\ \Leftrightarrow & & 5\cdot 0&=0\\ \Leftrightarrow & & 0&=0 \end{align}$

Sprinteraufgabe:

f) $\frac{3}{z+1}=-\frac{5}{2z-1}$

Versuche die Variablen mit Hilfe der Multiplikation aus dem Nenner zu bekommen.

$\begin{align} & & \frac{3}{z+1} &= - \frac{5}{2z-1} & & \mid \cdot (z+1)\\ \Leftrightarrow & & \frac{3}{z+1} \cdot (z+1) &= - \frac{5 \cdot (z+1)}{2z-1} & & \mid \text{kürzen}\\ \Leftrightarrow & & 3 &= - \frac{5 \cdot (z+1)}{2z-1} & & \mid \cdot (2z-1)\\ \Leftrightarrow & & 3 \cdot (2z-1) &= - \frac{5 \cdot (z+1)}{2z-1} \cdot (2z-1) & & \mid \text{kürzen}\\ \Leftrightarrow & & 3 \cdot (2z-1) &= - 5 \cdot (z+1) & &\\ \Leftrightarrow & & 6z-3 &= -5z-5 & & \mid +5z\\ \Leftrightarrow & & 11z-3 &= -5 & & \mid +3\\ \Leftrightarrow & & 11z &= -2 & & \mid :11\\ \Leftrightarrow & & z &= - \frac{2}{11}\\ & & \mathbb{L}=\{-\frac{2}{11}\} \end{align}$

Probe:

$\begin{align} & & \frac{3}{- \frac{2}{11} +1} &= - \frac{5}{2 \cdot (- \frac{2}{11}) -1} & &\\ \Leftrightarrow & & \frac{3}{\frac{9}{11}} &= - \frac{5}{- \frac{4}{11} -1} & &\\ \Leftrightarrow & & \frac{3}{\frac{9}{11}} &= - \frac{5}{- \frac{15}{11}} & & \mid \text{mit dem Kehrwert mal nehmen}\\ \Leftrightarrow & & 3 \cdot \frac{11}{9} &= - 5 \cdot - \frac{11}{15} & &\\ \Leftrightarrow & & \frac{33}{9} &= \frac{55}{15} & & \mid \text{kürzen}\\ \Leftrightarrow & & \frac{11}{3} &= \frac{11}{3} \end{align}$

Info

Auch für die Lösung quadratischer Gleichungen hast du Verfahren kennengelernt. Die Aufgaben helfen dir dabei, diese zu wiederholen.

Einfache quadratische Gleichungen

Löse die quadratischen Gleichungen ohne p-q-Formel. Nutze hierfür den Kasten zur Aufgabe in deinem Begleitmaterial. Kontrolliere deine Lösung.

a) $0=x^2-64$

b) $0=x^2+13x$

c) $-2x=\frac{1}{2}x^2$

zu a): Bei Gleichungen der Form $ax^2+c$, also ohne linearen Summanden $bx$ kannst du die Gleichung umstellen, sodass $x^2$ alleine steht und anschließend die Wurzel ziehen.

zu a): Achte beim Wurzelziehen auf die positive und negative Lösung.

zu b): Bei Gleichungen der Form $ax^2+bx$, also ohne konstanten Summanden $c$ kannst du $x$ ausklammern.

zu b): Ein Produkt ist genau dann $0$, wenn einer der beiden Faktoren bereits $0$ ist. Beispiel: ${\color{blue}x} \cdot ({\color{red}x-2})=0$ bedeutet, dass entweder ${\color{blue}x}=0$ oder ${\color{red}x-2}=0$ gilt.

zu c): Stelle um, sodass auf einer Seite des Gleichheitszeichen $0$ steht.

zu a) $\begin{alignat}{3} & & 0 &= x^2-64 \qquad &&| +64\\ &\Leftrightarrow \qquad & 64 &= x^2 &&| \sqrt{\text{ }}\\ &\Leftrightarrow &\pm 8 &= x &&\\ &\Leftrightarrow & x_1 &= -8 \text{ oder } x_2=8&& \end{alignat}$

zu b) $\begin{alignat}{5} & & & & 0 &= x^2+13x & & &&| x \text{ ausklammern}\\ &\Leftrightarrow \qquad & & & 0 &= x \cdot (x+13) & & &&| \text{einer der beiden Faktoren muss } 0 \text{ sein}\\ &\Leftrightarrow & 0 &= x_1 \qquad & \text{ o}&\text{der } & 0 &= x_2+13 \qquad &&|-13\\ &\Leftrightarrow & 0 &= x_1 & \text{ o}&\text{der } & -13 &= x_2 &&\\ &\Leftrightarrow & x_1 &= 0 & \text{ o}&\text{der } & x_2 &= -13 && \end{alignat}$

zu c)

$\begin{alignat}{5} & & & & -2x &= \frac{1}{2}x^2 & & &&| +2x\\ &\Leftrightarrow \qquad & & & 0 &= \frac{1}{2}x^2+2x & & &&| \cdot 2\\ &\Leftrightarrow & & & 0 &= x^2+4x & & &&| x \text{ ausklammern}\\ &\Leftrightarrow & & & 0 &= x \cdot (x+4) & & &&| \text{einer der beiden Faktoren muss } 0 \text{ sein}\\ &\Leftrightarrow & 0 &= x_1 \qquad & \text{ o}&\text{der } & 0 &= x_2+4 \qquad &&|-4\\ &\Leftrightarrow & 0 &= x_1 & \text{ o}&\text{der } & -4 &= x_2 &&\\ &\Leftrightarrow & x_1 &= 0 & \text{ o}&\text{der } & x_2 &= -4 && \end{alignat}$

Quadratische Gleichungen mit p-q-Formel

Löse die quadratischen Gleichungen. Nutze hierfür den Kasten zur Aufgabe in deinem Begleitmaterial. Kontrolliere deine Lösung.

a) $0=x^2+12x+27$

b) $0=x^2+6x-7$

c) $16x=x^2-17$

Verwende die p-q-Formel. Bringe die Gleichung also auf folgende Form $0=x^2+px+q$, lies dann $p$ und $q$ ab und bestimme die Lösung mit $x=-\frac{p}{2} \pm \sqrt{\left(\frac{p}{2}\right)^2 - q}$.

zu c): Stelle zunächst um, sodass auf einer Seite des Gleichheitszeichen $0$ steht.

zu a) $\begin{alignat}{3} & & 0 &= x^2+12x+27 &&| p=12, q=27\\ &\Leftrightarrow \qquad & x &= -\frac{12}{2} \pm \sqrt{\left(\frac{12}{2}\right)^2-27} \qquad &&\\ &\Leftrightarrow & x &= -6 \pm 3 &&\\ &\Leftrightarrow & x_1 &= -9 \text{ oder } x_2=3 && \end{alignat}$

zu b) $\begin{alignat}{3} & & 0 &= x^2+6x-7 &&| p=6, q=-7\\ &\Leftrightarrow \qquad & x &= -\frac{6}{2} \pm \sqrt{\left(\frac{6}{2}\right)^2-(-7)} \qquad &&\\ &\Leftrightarrow & x &= -3 \pm 4 &&\\ &\Leftrightarrow & x_1 &= -7 \text{ oder } x_2=1 && \end{alignat}$

zu c)

$\begin{alignat}{3} & & 16x &= x^2-17 &&| -16x\\ &\Leftrightarrow \qquad & 0 &= x^2-16x-17 &&| p=-16, q=-17\\ &\Leftrightarrow & x &= -\frac{-16}{2} \pm \sqrt{\left(\frac{-16}{2}\right)^2-(-17)} \qquad &&\\ &\Leftrightarrow & x &= 8 \pm 9 &&\\ &\Leftrightarrow & x_1 &= -1 \text{ oder } x_2=17 && \end{alignat}$

Vernetzte Aufgaben

Flächeninhalt

Klicke alle Terme an, die den Flächeninhalt der Fläche beschreiben.

Worin liegt der Unterschied zwischen Flächeninhalt und Umfang?

Mache dir bewusst, welche Bedeutung die einzelnen Glieder der Terme haben.

Zeichne die Rechtecke, die durch die einzelnen Term-Glieder repräsentiert werden, in dein Heft und überprüfe, ob sich daraus die Figur zusammen setzen lässt.

Zahlenrätsel

Aufgabe 3: Finde die gesuchte Zahl

Wenn man zur Zahl $12$ das Doppelte einer Zahl addiert, so erhält man das Vierfache der gesuchten Zahl. Stelle eine geeignete Gleichung auf und gib die gesuchte Zahl an.

Überlege dir, wie man das Doppelte und das Vierfache einer Zahl als Term schreibt.

Zunächst übersetzen wir die Informationen aus der Aufgabenstellung in eine mathematische Schreibweise:

Das Doppelte einer Zahl: $2x$

Zur Zahl $12$ das Doppelte einer Zahl addieren: $2x+12$. Dies wird die linke Seite der Gleichung bilden.

Das Vierfache der gesuchten Zahl: $4x$. Dies ist die rechte Seite der Gleichung.

Wir erhalten also die Gleichung: $2x+12=4x$.

Um das gesuchte $x$ zu finden, lösen wir die Gleichung, indem wir sie nach $x$ umstellen. Achte darauf alle Umformungen immer auf beiden Seiten der Gleichung durchzuführen.

$\begin{align}& & 2x+12 & = 4x & &\mid -2x\\ \Leftrightarrow & & 12 & = 2x & &\mid :2\\ \Leftrightarrow & & 6 & = x \end{align}$

Die gesuchte Zahl ist $6$.

Probe:

$\begin{align} & & 2\cdot 6+12&=4\cdot 6 \\ \Leftrightarrow & &24&=24 \end{align}$

Aufgabe 4: Alter der Mutter

Die Mutter von Leon ist $3$-mal so alt wie er. In $12$ Jahren wird sie doppelt so alt sein wie Leon. Wie alt sind Leon und seine Mutter heute?

Beachte, dass sich das doppelte Alter auf das Alter in $12$ Jahren bezieht.

Bezeichne mit $M$ das Alter der Mutter und mit $L$ das Alter von Leon. Die erste Gleichung ist $\begin{align}M=3L\end{align}$,da die Mutter von Leon 3-mal so alt ist wie er. Außerdem gilt die zweite Gleichung $\begin{align}M+12=2(L+12)\end{align}$. Die linke Seite der Gleichung beschreibt das Alter der Mutter in 12 Jahren. Dies entspricht der rechten Seite der Gleichung, da das Alter der Mutter in 12 Jahren dann das doppelte des Alters von Leon in 12 Jahren beträgt.

Setze nun $\begin{align}M=3L \end{align}$ in die zweite Gleichung ein:

$\begin{align}\\ \Leftrightarrow & & 3L+12&=2L+24 & &\mid -12\\ \Leftrightarrow & & 3L&=2L+12 & &\mid -2L\\ \Leftrightarrow & & L=12 \end{align}$

Leon ist heute also 12 Jahre alt. Um das Alter der Mutter zu bestimmen, setzten wir $L=12$ in die erste Gleichung ein:

$\begin{align} & & M=3 \cdot 12 = 36 \end{align}$

Die Mutter ist heute also 36 Jahre alt.

Probe erste Gleichung:

$\begin{align}\\ & & 3\cdot 12=36 & &\\ \Leftrightarrow & & 36=36 & \end{align}$

Probe zweite Gleichung:

$\begin{align}\\ & & 36+12=2\cdot(12+12) & &\\ \Leftrightarrow & & 48=48 & \end{align}$

Leon ist heute $12$ Jahre alt und seine Mutter ist heute $36$ Jahre alt.

Rechnen mit Gleichungen im Sachzusammenhang

Aufgabe 5: Zwei-Felder-Ball-Feld abstecken

Nick und Tom sollen für ein Sportfest ein Zwei-Felder-Ball-Feld abstecken. Dafür sollen sie ein $66$ m langes Seil und sechs Pfosten verwenden. Für das Umwickeln aller Pfosten werden insgesamt drei Meter Seil benötigt. Das Spielfeld soll aus zwei gleichgroßen quadratischen Flächen bestehen. Wie lang ist eine Seite von einer der quadratischen Flächen, wenn man davon ausgeht, dass Nick und Tom das gesamte Seil benutzen?

Um die Gleichung aufzustellen, benötigst du den Umfang des Spielfeldes.

Benutze die Skizze, um einen Term für den Umfang des Spielfeldes aufzustellen.

Skizzierung des Spielfeldes

Beachte, dass zusätzlich Seil für das Abspannen an den Pfosten benötigt wird.

Die gesuchte Seitenlänge bezeichnen wir mit $x$.

Skizzierung des Spielfeldes

Den Umfang des Spielfeldes erhalten wir durch den Term $7x$.

Wir erhalten die Gleichung: $7x+3=66$, da insgesamt $66$ Meter Seil zur Verfügung stehen und drei Meter Seil für die Abspannung an den Pfosten benötigt werden.

Diese Gleichung können wir lösen:

$\begin{align} & & 7x+3 &=66 & &\mid -3\\ \Leftrightarrow & & 7x &=63 & &\mid :7\\ \Leftrightarrow & & x &=9 \end{align}$

Probe:

$\begin{align} & & 7 \cdot 9 +3 &=66\\ \Leftrightarrow & & 63 + 3 &=66\\ \Leftrightarrow & & 66 &=66\\ \end{align}$

Eine Seite ist $9$ m lang.

Aufgabe 6: Getränkelager füllen

In einem Lager eines Restaurants sollen möglichst viele $35$ cm hohe Getränkekisten übereinander gestapelt werden. Die Raumhöhe beträgt $2,20$ m.

a) Wie viele Getränkekisten können übereinander gestapelt werden? Stelle eine Gleichung auf und berechne.

b) Eine Getränkekiste ist $40$ cm lang und $40$ cm breit. Das Lager hat eine Lagerfläche von $10$ m $\cdot$ $10$ m. Wie viele Getränkekisten finden insgesamt im Lager Platz?

Beachte die Umrechnung der Einheiten.

Berechne zuerst, wie viele Getränkekisten auf dem Boden der Lagerfläche Platz finden.

a) Zuerst wird die Höhe einer Getränkekiste in Meter umgerechnet: $35$ cm $=0,35$ m.

Jetzt kann die Gleichung aufgestellt werden: $0,35\cdot x=2,20$,

wobei $0,35$ die Höhe einer Getränkekiste in Metern und $2,20$ die Höhe des Lagerraumes in Metern angibt. Die Variable $x$ bezeichnet in der Gleichung die Anzahl der Kisten, die in den Lagerraum gestellt werden können.

Jetzt wird $x$ mit Hilfe der aufgestellten Gleichung berechnet:

$\begin{align} & & 0,35\cdot x &=2,20 & &\mid :0,35\\ \Leftrightarrow & & x &\approx 6,29 & &\\ \end{align}$

Probe:

$\begin{align} & & 0,35\cdot 6,29 \approx 2,20 & &\\ \Leftrightarrow & & 2,20 \approx 2,20 & &\\ \end{align}$

Das Ergebnis $6,29$ wird auf $6$ abgerundet, da nur ganze Kisten gestapelt werden können. Es können in dem Lagerraum also $6$ Getränkekisten übereinander gestapelt werden.

b) Zuerst legen wir den Boden der Lagerfläche mit Getränkekisten aus. Dazu stellen wir folgende Gleichung auf: $\begin{align} & & 10\cdot 10 &=0,4\cdot 0,4\cdot x & &\\ \Leftrightarrow & & 100 &=0,16\cdot x & &\mid :0,16\\ \Leftrightarrow & & 625 &=x \end{align}$

Probe:

$\begin{align} & & 10\cdot 10&=0,4\cdot 0,4\cdot 625 & &\\ \Leftrightarrow & & 100 &=0,16\cdot 625 & &\\ \Leftrightarrow & & 100 &=100 \end{align}$

In dieser Gleichung gibt der Teil $10\cdot 10$ die Grundfläche der Lagerfläche in m² an. Der Teil $0,4\cdot 0,4$ berechnet die Grundfläche der Getränkekisten in m². Die Variable $x$ bezeichnet die Anzahl der Getränkekisten.

Wir wissen nun also, dass $625$ Getränkekisten auf dem Boden der Lagerfläche Platz finden.

Aus Aufgabenteil a) wissen wir bereits, dass $6$ Getränkekisten übereinander gestapelt werden können. Also bleibt zu berechnen: $625\cdot 6=3750$.

Insgesamt finden demnach $3750$ Getränkekisten auf der Lagerfläche Platz.

Idee

Landwirt Mertens hat bisher eine quadratische Weide für seine paar Schafe. Da nun an dieser Stelle eine Landstraße ausgebaut werden soll, fragt die Stadt den Landwirt, ob er ein flächengleiches, rechteckiges Grundstück auf der anderen Seite seines Bauernhofes gegen seine quadratische Weide tauschen würde. Diese Weide ist zwar vier Meter kürzer, dafür aber sechs Meter länger.

Landwirt Mertens überlegt:

1. Hilf ihm und finde die Maße der Weiden heraus. Bearbeite diese Aufgabe in deinem Heft. Wenn du nicht weißt, wie du vorgehen sollst, schaue dir nach und nach die Tipps unten an.
2. Wie bist du vorgegangen, um die mathematische Gleichung zu lösen? Notiere deine Vorgehensweise im Heft.

Was ist gegeben?

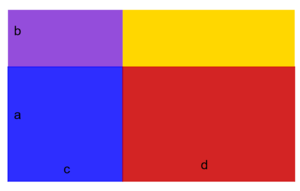
zwei flächengleiche Flächen (Quadrat und Rechteck)

x = Seitenlänge der quadratischen Weide

x - 4 = eine Seitenlänge der rechteckigen Weide (3m kürzer)

x + 6 = andere Seitenlänge der rechteckigen Weide (5m länger)

Versuche nun eine Gleichung aufzustellen.

Die beiden Weiden sind flächengleich, d.h. ihr Flächeninhalt ist gleich.

Benutze zum Aufstellen der Gleichung die Formeln für die Berechnung des Flächeninhaltes eines Quadrats und eines Rechtecks.

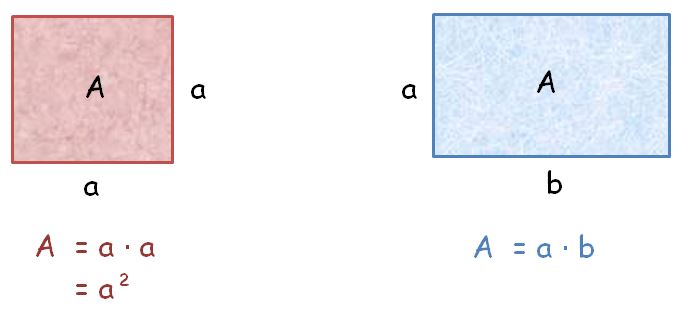
Beide Flächen sind gleich groß, daher lautet die Gleichung:

x² = (x – 4) (x + 6)

Versuche nun x zu berechnen. Löse hierfür zunächst die Klammern auf.

Du hast nun herausgefunden, dass die Länge und Breite der quadratischen Weide je 12m beträgt. Damit kannst du jetzt die Seitenlängen der rechteckigen Weide berechnen. Setze hierfür x = 12 in deine aufgestellten Terme ein:

• x - 4 (eine Seitenlänge des Rechtecks)
• x + 6 (andere Seitenlänge des Rechtecks)