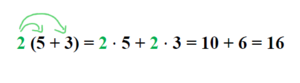Jule Volbers/Testseite

Willkommen auf dem Lernpfad: Nützliche Werkzeuge - Terme und Gleichungen.

In diesem Lernpfad geht es um das Vertiefen deines Wissens über Terme, Variablen und Gleichungen. Du findest hier eine Wiederholung zu den Begriffen und Übungsaufgaben zu den Themen Terme aufstellen, Terme umformen und Gleichungen lösen. .

1.Terme, Variablen und Gleichungen

Was ist Was?" - Wiederhole die Begriffe!

Ergänze den Lückentext. Prüfe das Ergebnis und übertrage die Lösung in den Kasten "Terme, Variablen und Gleichungen" in deinem Begleitmaterial.

Variablen sind Zeichen (meistens kleine Buchstaben). Sie sind Platzhalter. Du kannst Zahlen für sie einsetzen. Terme sind Rechenausdrücke. Terme können Zahlen, Rechenzeichen, Klammern und Variable enthalten. Werden zwei Terme mit einem Gleichheitszeichen verbunden, entsteht eine Gleichung. Es gibt verschiedene Arten von Gleichungen. Wichtige Arten sind die linearen und die quadratischen Gleichungen.

Begriffstraining

Teste dein Wissen!

 

2.Terme

Terme aufstellen

Terme in Sachsituationen

Du hast gelernt, Sachsituationen mit Hilfe von Termen zu beschreiben. Hier kannst du dein Wissen testen.

a)

b)

Terme vereinfachen

Info

Terme enthalten unterschiedliche Rechenoperationen wie Addition, Subtraktion, Multiplikation und Division. Manche Teile von Termen kann man zusammenfassen, um so den Term zu vereinfachen. Du hast die Regeln im Unterricht bereits kennengelernt.

Erinnerung: Überflüssige Malpunkte

Um Produktterme so einfach wie möglich zu schreiben, dürfen überflüssige Malpunkte weggelassen werden. Dies sind Malpunkte zwischen einer Zahl und einer Variablen und zwischen einer Zahl oder Variablen und einer Klammer.Markiere die überflüssigen Malpunkte in den Termen.

Info

Überflüssige Malpunkte werden nicht notiert.

Terme zusammenfassen

Vereinfache die Terme soweit wie möglich. Wenn du dir unsicher bist, schaue dir die Tipps an.
Zusammenfassen von Summen:
a) $2a+10a+11+7$
b) $-4x+5+9x-7$
c) $3a+5a +7b-2b$
d) $-2c+15-4d-3c-5$
e) $13x^2+3x+9y-3y$
f) $2x+xy-3y-2xy+2xy^2$

Beim Zusammenfassen von Summen gilt:

• Nur gleiche Variablen dürfen zusammengefasst werden.
• Auch die Potenz muss übereinstimmen.
• Die Rechenregeln für das Rechnen mit ganzen Zahlen müssen beachtet werden.
• Es kann helfen, gleiche Summanden farbig zu markieren.

Beispiele:
1) ${\color{blue}b}{\color{red}+a+3a}$ $= {\color{blue}b}{\color{red}+4a}$

2) ${\color{orange}2x}{\color{red}+xy}{\color{blue}-3y}{\color{red}-2xy}{\color{green}+2xy^2}$ $= {\color{orange}2x}{\color{blue}-3y}{\color{green}+2xy^2}{\color{red}+xy-2xy}$ $= {\color{orange}2x}{\color{blue}-3y^2}{\color{green}+2xy^2}{\color{red}-xy}$

Hier konnten nur die beiden Teile mit ${\color{red}xy}$ zusammengefasst werden, da alle anderen Variablen unterschiedlich sind bzw. in einer anderen Potenz vorkommen.

Zusammenfassen von Produkten
f) $5{r} 4{r}{s}$
g) $2{x}(-7{x^2y})(-3{y^3})$

Beim Zusammenfassen von Produkten gilt:

• Es können auch Teile mit unterschiedlichen Potenzen oder Variablen zusammengefasst werden.
  
• Der Multiplikationspunkt muss nicht notiert werden ${2}\cdot {a}$ = 2a
  
• Beachte die Vorzeichen der Faktoren!

a) $2a+10b+11+7$ = $12a+18$
b) $-4x+5+9x-7$= $5x-2$
c) $3a+5a+7b-2b$ = $8a+5b$
d) $-2c+15-4d-3c-5$= $-5c-4d+10$
e) $13x^2+3x^2+9y-3y$= $13x^2+3x^2+9y-3y$
f) $5{r}4{r}{s}$ $= 5 \cdot 4 {x} {x} {y}$ $= 20 {x^2}{y}$

g) $2{x}(-7{x^2y})(-3{y^3})$ $= 2 \cdot (-7) \cdot (-3) {x} {x^2} {y} {y^3}$ $= 42{x^3}{y^4}$

Idee

Wichtig: Unterscheide
$(-x) + (-x) = -2x$
$(-x) \cdot (-y) = x \cdot y$

Denke daran. Es gilt:
$+ \cdot +$ ergibt: $+$
$- \cdot -$ ergibt: $+$
$- \cdot +$ ergibt: $-$
$+ \cdot -$ ergibt: $-$

Beachte außerdem die Vorfahrtsregeln: Potenz- vor - Punkt- vor Strichrechnung, die Klammer geht immer vor.

Termtraining.

Füge die zugehörigen Terme zusammen. Du kannst hierfür deinen Stift und Papier nutzen.

 

Klammern in Termen

Klammern auflösen:

Das Ausmultiplizieren hat zum Ziel, eine Klammer aufzulösen.

Auflösen von Klammern

Erkläre mit Hilfe der Abbildung, dass für das Auflösen von Klammern gilt:

${\color{green}a}(b+c) = {\color{green}a}b + {\color{green}a}c$.

$(b+c){\color{green}a} = b{\color{green}a} + {\color{green}a}$.

Formuliere die Regel in eigenen Worten. Wende sie auf das Beispiel a = 2, b  = 5 und c = 3 an. Kontrolliere dann deine Lösung.

Man multipliziert einen Faktor mit einer Klammer, indem man den Faktor mit jedem einzelnen Glied in der Klammer multipliziert.

Es spielt keine Rolle, ob der Faktor links oder rechts von der Klammer steht:

$(5+3) \cdot {\color{green}2} = 5 \cdot {\color{green}2} + 3\cdot {\color{green}2} = 10 + 6 = 16$.

thumb

Erinnerung

1. Achte darauf, ob in der Klammer eine Summe oder Differenz steht, denn: $a(b{\color{red}-}c) = a \cdot b {\color{red}-} a\cdot c$

1. Bei Minusklammern, also wenn vor der Klammer ein negativer Faktor steht, drehen sich die Vorzeichen von jedem Glied in der Klammer um:

${\color{red}-}a(b{\color{red}+}c) = {\color{red}-}ab {\color{red}-} ac$.

${\color{red}-}a({\color{red}-}b{\color{red}+}c) = ab {\color{red}-} ac$.

Klammern in Termen

Ergänze den Lückentext. Prüfe das Ergebnis und übertrage die Lösung in den Kasten "Klammern in Termen" in deinem Begleitmaterial. Das Ausmultiplizieren hat zum Ziel, eine Klammer aufzulösen. Man multipliziert einen Faktor mit einer Klammer, indem man den Faktor mit jedem einzelnen Glied in der Klammer multipliziert. ${\color{green}a}(b+c) =''' {\color{green}a}b''' + '''{\color{green}a}c$. Dies nennt man Distributivgesetz.
Es spielt keine Rolle, ob der Faktor links oder rechts von der Klammer steht: $(b+c) \cdot {\color{green}a} = b \cdot {\color{green}a} + c\cdot {\color{green}a} = ac + bc$. Zwei Summen (oder Differenzen) werden miteinander multipliziert, indem man jeden Summanden der ersten Klammer mit jedem Summanden der zweiten Klammer multipliziert: $(a+b)(c+d) ='''ac''' + ad + bc + bd$.

Aufgabe

In dieser Aufgabe kannst du das Ausmultiplizieren üben. Ordne jedem Klammerterm die richtige ausmultiplizierte Lösung zu. Nimm dir einen Zettel für Nebenrechnungen zur Hilfe.

a) $(5b+c+3d)\cdot a =$ $5ab+ac+3ad$
b) $(5a+4b)\cdot 4 =$ $16b+20a$
c) $-8(a-2b) =$ $16b-8a$
d) $(2x+5)(3x-7) =$ $6x^2+x-35$
d) $(5a+10b)(\frac{1}{5}c+2d) =$ $ac+10ad+2bc+20bd$
f) $-\frac{1}{2}(\frac{1}{2}a+\frac{1}{2}b) =$ $-\frac{1}{4}a-\frac{1}{4}b$

Ausklammern Beim Ausklammern wird eine Summe in ein Produkt umgewandelt, es werden also Klammern hinzugefügt. Dies ist nur dann möglich, wenn die Summanden gemeinsame Faktoren haben.

Ausklammern

Gemeinsame Faktoren in einer Summe können ausgeklammert werden.
Beispiel:
8x + 12xy
= 4x⋅2 + 4x⋅3y

= 4x⋅(2 + 3y)

Übung 8 Ausklammern

Suche in den LearningApps nach gemeinsamen Faktoren der Summenden und klammere diese dann aus.

3. Gleichungen

Aufgabe 1: Waagschalenvergleich

Unten kannst du eine Waage sehen. Anfangs ist die Waage für einen festen Wert für $x$ unausgeglichen. Durch das Hinzufügen von Kugeln oder $x$ auf beiden Seiten kann ein Gleichgewicht erzielt werden. Dabei kann durch Probieren herausgefunden werden, welchen Wert $x$ hat. Klickst du auf "neues $x$", wird ein neuer Wert für $x$ bestimmt.

a) Bringe die Waage ins Gleichgewicht. Wie gehst du vor? Wiederhole die Aufgabe für verschiedene Werte von $x$, indem du auf "neues $x$" klickst.

Die Waage kann ins Gleichgewicht gebracht werden, indem auf der rechten Seite nach und nach Kugeln hinzugefügt oder entfernt werden bis die Waage ausgeglichen ist. Dann kannst du abzählen, wie viele Kugeln mehr auf der Seite ohne $x$ sind. Diese Zahl ist das gesuchte $x$.

b) Die Waage steht immer noch im Gleichgewicht. Füge nun ein [zwei] weitere $x$ zur linken Waagschale hinzu. Wie gehst du jetzt vor?

Fügst du ein [zwei] weiteres $x$ zur linken Seite hinzu, so müssen doppelt [dreimal] so viele Kugeln zur rechten Seite hinzugefügt werden wie vorher. Wurden also bei einem $x$ auf der linken Waagschale nur drei Kugeln hinzugefügt, sind es bei zwei $x$ sechs Kugeln.

c) Bringe die Waage ins Gleichgewicht. Nimm dann auf beiden Seiten der Waage gleich viele Kugeln weg. Was kannst du beobachten?

Werden auf beiden Seiten der Waage gleich viele Kugeln entfernt, bleibt die Waage im Gleichgewicht.

Aufgabe 2: Lösungsmenge bestimmen

Bestimme die Lösungsmenge der Gleichung. Führe, wenn möglich, eine Probe durch. Denke daran: Eine Probe kann nur durchgeführt werden, wenn es mindestens eine Lösung für die Gleichung gibt.

Beispiel 1: Richtig Gleichungen lösen

Um eine Gleichung zu lösen, wird sie zunächst nach der Variable aufgelöst. Diese Variable soll am Ende isoliert, d.h. alleine, auf einer Seite der Gleichung stehen. Wir schauen uns ein Beispiel an:

$3y+5=y+35$.

Um diese Gleichung zu lösen, bringen wir zunächst alle $y$ auf eine Seite der Gleichung.

$\begin{align} && 3y+5&=y+35 & &\mid -y\\ \Leftrightarrow & & 2y+5&=35\\ \end{align}$

Jetzt können wir wie gewohnt nach $y$ auflösen.

$\begin{align} & & 2y+5&=35 & &\mid -5\\ \Leftrightarrow & & 2y&=30 & &\mid :2\\ \Leftrightarrow & & y&=15 \end{align}$

Probe:

$\begin{align} & &(3\cdot 15)+5&=15+35\\ \Leftrightarrow & & 45+5 &=50\\ \Leftrightarrow & & 50 &=50 \end{align}$

Wir erhalten also die Lösungsmenge $\mathbb{L}=\{15\}$.

Wenn du nicht mehr weißt, was die Lösungsmenge ist, schau bei den Definitionen nach.

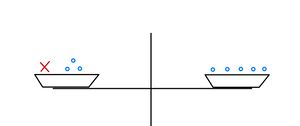
a) Löse die Gleichung anschaulich mittels Skizzen von Waagen in deinem Heft: $x+3=5$

Überlege dir, wie die Waage im Gleichgewicht aussieht.

Beide Seiten der Gleichung sind gleichwertig. Also ist die Waage im Gleichgewicht.

Waage im Gleichgewicht

Die Waage bleibt im Gleichgewicht wenn gleich viele Kugeln auf beiden Seiten ergänzt oder entfernt werden. Wir entfernen jeweils drei Kugeln.

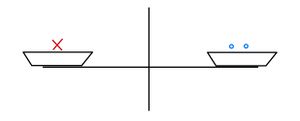
Waage nach Durchführung einer Umformung

$\begin{align} & & x+3 &=5 & &\mid -3\\ \Leftrightarrow & & x &=2 \end{align}$

Probe:

$\begin{align} & & 2+3 &=5 \\ \Leftrightarrow & & 5 &=5 \end{align}$

Wir erhalten die Lösungsmenge $\mathbb{L}=\{2\}$.

b) $a-64=5$

Versuche die Gleichung so umzustellen, dass auf der einen Seite des Gleichheitszeichens nur noch das $a$ steht.

$\begin{align} & & a-64 &=5 & &\mid +64\\ \Leftrightarrow & & a &=69 \\ & & \mathbb{L}=\{69\} \end{align}$

Probe:

$\begin{align} & & 69-64 &=5 \\ \Leftrightarrow & & 69-64 &=5\\ \Leftrightarrow & & 5 &=5 \end{align}$

c) $3x+7=16$

Versuche zunächst die Gleichung so umzustellen, dass auf der einen Seite nur noch das $x$ mit dem Faktor steht.

$\begin{align} & & 3x+7&=16 & &\mid -7\\ \Leftrightarrow & & 3x &=9 & &\mid :3\\ \Leftrightarrow & & x &=3\\ & & \mathbb{L}=\{3\} \end{align}$

Probe:

$\begin{align} & & 3\cdot 3+7&=16\\ \Leftrightarrow & & 9+7 &=16\\ \Leftrightarrow & & 16 &=16 \end{align}$

d) $d\cdot (d-5)=0$

Überlege dir, was für zwei Faktoren gilt, deren Produkt $0$ ist.

Ein Produkt ist dann $0$, wenn einer der Faktoren $0$ ist. Deshalb kann man die Aufgabe so lösen:

$\begin{align} & & d\cdot (d-5)&=0\\ \Leftrightarrow & & d=0 &\text{ oder } d-5=0\\ \Leftrightarrow & & d=0 &\text{ oder } d=5\\ & & \mathbb{L}=\{0,5\} \end{align}$

Probe:

$\begin{align} & & 0\cdot (0-5)&=0\\ \Leftrightarrow & & 0&=0 \end{align}$

$\begin{align} & & 5\cdot (5-5)&=0\\ \Leftrightarrow & & 5\cdot 0&=0\\ \Leftrightarrow & & 0&=0 \end{align}$

e) $4(x+1)-4x-5=1$

Löse zuerst die Klammer auf.

$\begin{align} & & 4(x+1)-4x-5 &=1\\ \Leftrightarrow & & 4x+4-4x-5 &=1\\ \Leftrightarrow & & 4x-4x+4-5 &=1\\ \Leftrightarrow & & -1 &=1 \end{align}$

Das ist ein Widerspruch. Deshalb ist die Lösungsmenge leer: $\mathbb{L}=\{\}$. Hier ist keine Probe durch Einsetzen möglich, weil die Lösungsmenge leer ist.

f) $\frac{1}{2x}=0,5$

Versuche die Gleichung so umzustellen, dass du Brüche kürzen kannst.

$\begin{align} & & \frac{1}{2x} &=0,5 & & \mid \cdot 2x\\ \Leftrightarrow & & \frac{1}{2x} \cdot 2x &= 0,5 \cdot 2x & & \mid \text{kürzen}\\ \Leftrightarrow & & 1 &=0,5\cdot 2x & & \mid :0,5\\ \Leftrightarrow & & \frac{1}{0,5} &=\frac{0,5}{0,5} \cdot 2x & & \mid \text{kürzen}\\ \Leftrightarrow & & 2 &=2x & &\mid :2\\ \Leftrightarrow & & 1 &=x\\ & & \mathbb{L}=\{1\} \end{align}$

Probe:

$\begin{align} & & \frac{1}{2 \cdot 1} &=0,5 & &\\ \Leftrightarrow & & \frac{1}{2} &=0,5 & &\\ \Leftrightarrow & & 0,5 &=0,5 \end{align}$

g) $\frac{3}{z+1}=-\frac{5}{2z-1}$

Versuche die Variablen mit Hilfe der Multiplikation aus dem Nenner zu bekommen.

$\begin{align} & & \frac{3}{z+1} &= - \frac{5}{2z-1} & & \mid \cdot (z+1)\\ \Leftrightarrow & & \frac{3}{z+1} \cdot (z+1) &= - \frac{5 \cdot (z+1)}{2z-1} & & \mid \text{kürzen}\\ \Leftrightarrow & & 3 &= - \frac{5 \cdot (z+1)}{2z-1} & & \mid \cdot (2z-1)\\ \Leftrightarrow & & 3 \cdot (2z-1) &= - \frac{5 \cdot (z+1)}{2z-1} \cdot (2z-1) & & \mid \text{kürzen}\\ \Leftrightarrow & & 3 \cdot (2z-1) &= - 5 \cdot (z+1) & &\\ \Leftrightarrow & & 6z-3 &= -5z-5 & & \mid +5z\\ \Leftrightarrow & & 11z-3 &= -5 & & \mid +3\\ \Leftrightarrow & & 11z &= -2 & & \mid :11\\ \Leftrightarrow & & z &= - \frac{2}{11}\\ & & \mathbb{L}=\{-\frac{2}{11}\} \end{align}$

Probe:

$\begin{align} & & \frac{3}{- \frac{2}{11} +1} &= - \frac{5}{2 \cdot (- \frac{2}{11}) -1} & &\\ \Leftrightarrow & & \frac{3}{\frac{9}{11}} &= - \frac{5}{- \frac{4}{11} -1} & &\\ \Leftrightarrow & & \frac{3}{\frac{9}{11}} &= - \frac{5}{- \frac{15}{11}} & & \mid \text{mit dem Kehrwert mal nehmen}\\ \Leftrightarrow & & 3 \cdot \frac{11}{9} &= - 5 \cdot - \frac{11}{15} & &\\ \Leftrightarrow & & \frac{33}{9} &= \frac{55}{15} & & \mid \text{kürzen}\\ \Leftrightarrow & & \frac{11}{3} &= \frac{11}{3} \end{align}$

Quadratische Gleichungen lösen

15. Einfache quadratische Gleichungen

Löse die quadratischen Gleichungen </nowiki>ohne p-q-Formel.

a) $0=x^2-64$

b) $0=x^2+13x$

c) $-2x=\frac{1}{2}x^2$

zu a): Bei Gleichungen der Form $ax^2+c$, also ohne linearen Summanden $bx$ kannst du die Gleichung umstellen, sodass $x^2$ alleine steht und anschließend die Wurzel ziehen.

zu a): Achte beim Wurzelziehen auf die positive und negative Lösung.

zu b): Bei Gleichungen der Form $ax^2+bx$, also ohne konstanten Summanden $c$ kannst du $x$ ausklammern.

zu b): Ein Produkt ist genau dann $0$, wenn einer der beiden Faktoren bereits $0$ ist. Beispiel: ${\color{blue}x} \cdot ({\color{red}x-2})=0$ bedeutet, dass entweder ${\color{blue}x}=0$ oder ${\color{red}x-2}=0$ gilt.

zu c): Stelle um, sodass auf einer Seite des Gleichheitszeichen $0$ steht.

zu a) $\begin{alignat}{3} & & 0 &= x^2-64 \qquad &&| +64\\ &\Leftrightarrow \qquad & 64 &= x^2 &&| \sqrt{\text{ }}\\ &\Leftrightarrow &\pm 8 &= x &&\\ &\Leftrightarrow & x_1 &= -8 \text{ oder } x_2=8&& \end{alignat}$

zu b) $\begin{alignat}{5} & & & & 0 &= x^2+13x & & &&| x \text{ ausklammern}\\ &\Leftrightarrow \qquad & & & 0 &= x \cdot (x+13) & & &&| \text{einer der beiden Faktoren muss } 0 \text{ sein}\\ &\Leftrightarrow & 0 &= x_1 \qquad & \text{ o}&\text{der } & 0 &= x_2+13 \qquad &&|-13\\ &\Leftrightarrow & 0 &= x_1 & \text{ o}&\text{der } & -13 &= x_2 &&\\ &\Leftrightarrow & x_1 &= 0 & \text{ o}&\text{der } & x_2 &= -13 && \end{alignat}$

zu c)

$\begin{alignat}{5} & & & & -2x &= \frac{1}{2}x^2 & & &&| +2x\\ &\Leftrightarrow \qquad & & & 0 &= \frac{1}{2}x^2+2x & & &&| \cdot 2\\ &\Leftrightarrow & & & 0 &= x^2+4x & & &&| x \text{ ausklammern}\\ &\Leftrightarrow & & & 0 &= x \cdot (x+4) & & &&| \text{einer der beiden Faktoren muss } 0 \text{ sein}\\ &\Leftrightarrow & 0 &= x_1 \qquad & \text{ o}&\text{der } & 0 &= x_2+4 \qquad &&|-4\\ &\Leftrightarrow & 0 &= x_1 & \text{ o}&\text{der } & -4 &= x_2 &&\\ &\Leftrightarrow & x_1 &= 0 & \text{ o}&\text{der } & x_2 &= -4 && \end{alignat}$

16. Quadratische Gleichungen mit Standardverfahren

Löse die quadratischen Gleichungen.</nowiki>

a) $0=x^2+12x+27$

b) $0=x^2+6x-7$

c) $16x=x^2-17$

Verwende die p-q-Formel. Bringe die Gleichung also auf folgende Form $0=x^2+px+q$, lies dann $p$ und $q$ ab und bestimme die Lösung mit $x=-\frac{p}{2} \pm \sqrt{\left(\frac{p}{2}\right)^2 - q}$.

zu c): Stelle zunächst um, sodass auf einer Seite des Gleichheitszeichen $0$ steht.

zu a) $\begin{alignat}{3} & & 0 &= x^2+12x+27 &&| p=12, q=27\\ &\Leftrightarrow \qquad & x &= -\frac{12}{2} \pm \sqrt{\left(\frac{12}{2}\right)^2-27} \qquad &&\\ &\Leftrightarrow & x &= -6 \pm 3 &&\\ &\Leftrightarrow & x_1 &= -9 \text{ oder } x_2=3 && \end{alignat}$

zu b) $\begin{alignat}{3} & & 0 &= x^2+6x-7 &&| p=6, q=-7\\ &\Leftrightarrow \qquad & x &= -\frac{6}{2} \pm \sqrt{\left(\frac{6}{2}\right)^2-(-7)} \qquad &&\\ &\Leftrightarrow & x &= -3 \pm 4 &&\\ &\Leftrightarrow & x_1 &= -7 \text{ oder } x_2=1 && \end{alignat}$

zu c)

$\begin{alignat}{3} & & 16x &= x^2-17 &&| -16x\\ &\Leftrightarrow \qquad & 0 &= x^2-16x-17 &&| p=-16, q=-17\\ &\Leftrightarrow & x &= -\frac{-16}{2} \pm \sqrt{\left(\frac{-16}{2}\right)^2-(-17)} \qquad &&\\ &\Leftrightarrow & x &= 8 \pm 9 &&\\ &\Leftrightarrow & x_1 &= -1 \text{ oder } x_2=17 && \end{alignat}$

17. Fortgeschrittene quadratische Gleichungen mit Standardverfahren

Löse die quadratischen Gleichungen.</nowiki>

a) $0=4x^2+40x+36$

b) $14x=7x^2-56$

c) $14x=3x^2+2x-15$

Um die p-q-Formel verwenden zu können muss vor dem $x^2$ der Vorfaktor $1$ (der in der Regel nicht ausgeschrieben wird) stehen.

Steht vor dem $x^2$ ein anderer Vorfaktor als $1$, so dividiere beide Seiten der Gleichung durch diesen Vorfaktor.

zu a) $\begin{alignat}{3} & & 0 &= 4x^2+40x+36 &&| \colon 4\\ &\Leftrightarrow \qquad & 0 &= x^2+10x+9 &&| p=10, q=9\\ &\Leftrightarrow & x &= -\frac{10}{2} \pm \sqrt{\left(\frac{10}{2}\right)^2-9} \qquad &&\\ &\Leftrightarrow & x &= -5 \pm 4 &&\\ &\Leftrightarrow & x_1 &= -9 \text{ oder } x_2=-1 && \end{alignat}$

zu b) $\begin{alignat}{3} & & 14x &= 7x^2-56 &&| -14x\\ &\Leftrightarrow \qquad & 0 &= 7x^2-14x-56 &&| \colon 7\\ &\Leftrightarrow & 0 &= x^2-2x-8 &&| p=-2, q=-8\\ &\Leftrightarrow & x &= -\frac{-2}{2} \pm \sqrt{\left(\frac{-2}{2}\right)^2-(-8)} \qquad &&\\ &\Leftrightarrow & x &= 1 \pm 3 &&\\ &\Leftrightarrow & x_1 &= -2 \text{ oder } x_2=4 && \end{alignat}$

zu c)

$\begin{alignat}{3} & & 14x &= 3x^2+2x-15 &&| -14x\\ &\Leftrightarrow \qquad & 0 &= 3x^2-12x-15 &&| \colon 3\\ &\Leftrightarrow & 0 &= x^2-4x-5 &&| p=-4, q=-5\\ &\Leftrightarrow & x &= -\frac{-4}{2} \pm \sqrt{\left(\frac{-4}{2}\right)^2-(-5)} \qquad &&\\ &\Leftrightarrow & x &= 2 \pm 3 &&\\ &\Leftrightarrow & x_1 &= -1 \text{ oder } x_2=5 && \end{alignat}$

Vernetzte Aufgaben

1. Flächeninhalt

Klicke alle Terme an, die den Flächeninhalt der Fläche beschreiben.

Worin liegt der Unterschied zwischen Flächeninhalt und Umfang?

Mache dir bewusst, welche Bedeutung die einzelnen Glieder der Terme haben.

Zeichne die Rechtecke, die durch die einzelnen Term-Glieder repräsentiert werden, in dein Heft und überprüfe, ob sich daraus die Figur zusammen setzen lässt.