Benutzer:Buss-Haskert/Exponentialfunktion/exponentielles Wachstum: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
K (Navigation) Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 2: | Zeile 2: | ||
SEITE IM AUFBAU | SEITE IM AUFBAU | ||
{{Navigation|[[Benutzer:Buss-Haskert/Exponentialfunktion|1) | {{Navigation|[[Benutzer:Buss-Haskert/Exponentialfunktion|Vorwissen]]<br>[[Benutzer:Buss-Haskert/Exponentialfunktion/Wachstum| 1) Lineares und exponentielles Wachstum (Einstieg)]]<br>[[Benutzer:Buss-Haskert/Exponentialfunktion/Wachstum|2) Wachstumsrate und Wachstumsfaktor ]]<br>[[Benutzer:Buss-Haskert/Exponentialfunktion/exponentielles Wachstum|3) Exponentielles Wachstum]]}} | ||
<br> | <br> | ||
Version vom 27. Dezember 2021, 10:30 Uhr
SEITE IM AUFBAU
Vorwissen
1) Lineares und exponentielles Wachstum (Einstieg)
2) Wachstumsrate und Wachstumsfaktor
3) Exponentielles Wachstum
1) Lineares und exponentielles Wachstum (Einstieg)
2) Wachstumsrate und Wachstumsfaktor
3) Exponentielles Wachstum
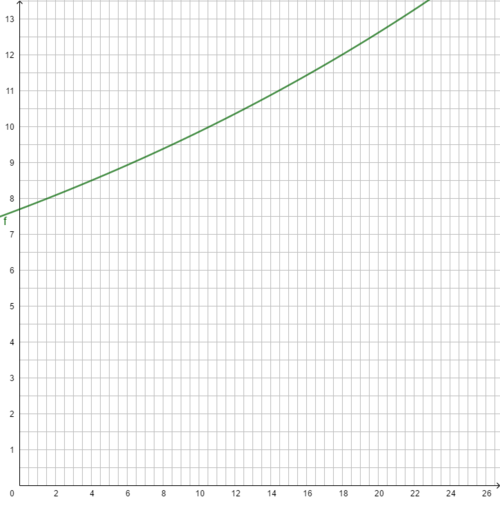
3 Exponentielles Wachstum
Prognose für das Jahr 2030: n = 11
W11 = W0 ∙ q11
= 7,70 ∙ 1,02511
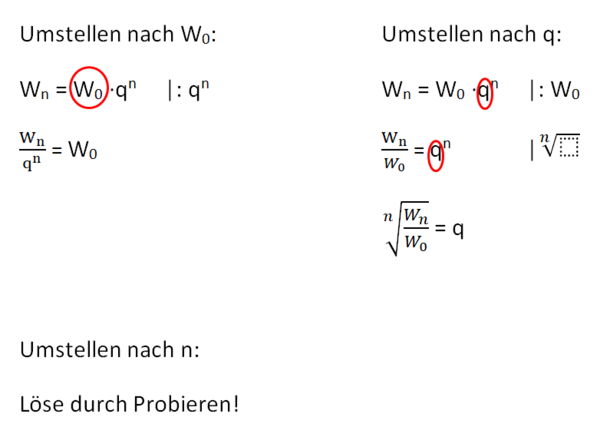
Die Gleichung Wn = W0 · qn heißt Exponentialgleichung, da die Variable n im Exponenten steht.
ÜBUNGSAUFGABEN ERGÄNZEN
- Formel umstellen
- Verdopplungszeit (Bakterien)

Applet von Hegius, R. Schürz
- Halbwertszeit (Atome)

Applet von Hegius, R. Schürz
4 Die Exponentialfunktion

Applet von Ralf Wagner
Der Graph verläuft immer oberhalb der x-Achse.
Der Graph geht immer durch den Punkt (0|1).
Für a>1 steigt der Graph (Zunahme),