Benutzer:Buss-Haskert/Exponentialfunktion/exponentielles Wachstum

zurück zur Seite der Herta-Lebenstein-Realschule

SEITE IM AUFBAU

1) Vorwissen
2) Wachstum und Abnahme
3) Exponentielles Wachstum

3 Exponentielles Wachstum

Einstieg: Weltbevölkerung

Im Jahr 2019 lebten 7,7 Mrd. Menschen auf der Erde. Wissenschaflter prognostizierten in diesem Jahr eine jährliche Zuwachsrate von 1,25%.
Also gilt q=100%+1,25% = 101,25% = 1,0125

Wie viele Menschen leben demnach im Jahr 2030 auf der Erde?

Stelle diese Situation auf verschiedene Arten dar. (Erinnerung: Text (ist gegeben), Wertetabelle, Funktionsgleichung und Funktionsgraph)

Datei:Weltbevölkerung Tipp Wertetabelle.png

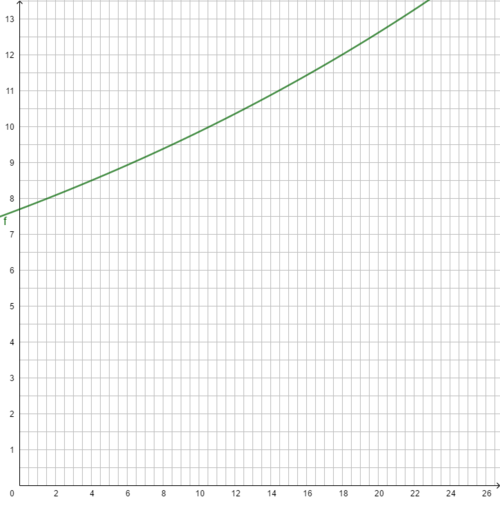
Prognose für das Jahr 2030: n = 11
W₁₁ = W₀ ∙ q¹¹
   = 7,70 ∙ 1,025¹¹

   ≈8,83

Exponentielles Wachstum - Exponentialgleichung

Wir sprechen von exponentiellem Wachstum, wenn der Wert einer Größe in gleichen Zeitspannen immer um denselben Prozentsatz p% zunimmt bzw. abnimmt.
Die neue Größe nach n Zeitspannen berechnen wir mit
W_n = W₀ · qⁿ,

wobei q der Wachstumsfaktor ist. q = 1+p% (Zunahmen) bzw.q=1-p%(Abnahme)

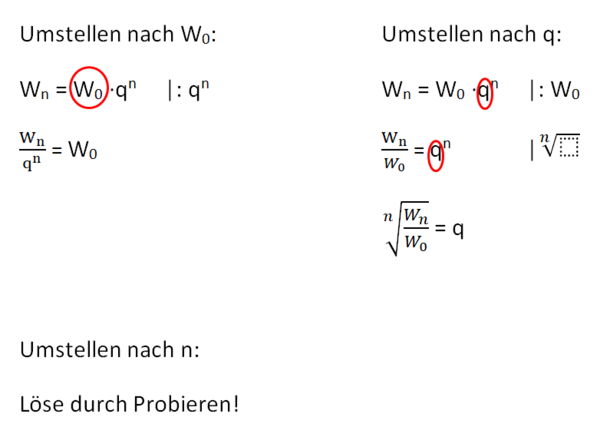
Die Gleichung W_n = W₀ · qⁿ heißt Exponentialgleichung, da die Variable n im Exponenten steht.

Anwendungsaufgabe 1: Erdbevölkerung

...(Anwendung, Wn gesucht)

Anwendungsaufgabe 2: Klimawandel

...(Anwendung W0 gesucht)

Exponentialgleichung - Formel umstellen

Anwendungsaufgabe 3

...(Anwendung q gesucht)

Anwendungsaufgabe 4

...(Anwendung n gesucht)

ÜBUNGSAUFGABEN ERGÄNZEN

• Formel umstellen
• Verdopplungszeit (Bakterien)

Applet von Hegius, R. Schürz

• Halbwertszeit (Atome)

Applet von Hegius, R. Schürz

4 Die Exponentialfunktion

Exponentialfunktion

Die Funktion mit der Gleichung f(x) = c∙ax heißt Exponentialfunktion.

Eigenschaften der Exponentialfunktion

Beschreibe die Eigenschaften der Exponentialfunktion f(x) = c∙ax .

Wähle zunächst c=1. Wie verläuft der Graph der Funktion? Löse den Lückentext und übertrage ihn in dein Heft.

Applet von Ralf Wagner

Der Graph verläuft immer oberhalb der x-Achse.
Der Graph geht immer durch den Punkt (0|1).
Für a>1 steigt der Graph (Zunahme),

für 0<a<1 fällt der Graph (Abnahme).