Benutzer:Buss-Haskert/Exponentialfunktion/Wachstum

Wachstum und Abnahme

Überlegt, wo es in eurer Umgebung Wachstum bzw. Abnahme gibt.

Gibt es ein Modell, das dieses Wachstum beschreibt?

Mögliche Antworten:

• Bevölkerungswachstum
• Bakterienwachstum
• Haarwachstum
• Druckzunahme je nach Meerestiefe
• Temperaturanstieg
• Sprunghöhe Flummi
• Zerfall von Bierschaum
• Kerzenhöhe je nach Dauer
• Lichtintensität
• Wertverlust bei Neuwagen

Wachstum und Abnahme

Wir sprechen von positivem Wachstum, wenn in gleichen Zeitabschnitten der neue Wert größer ist als der alte Wert.
Wir sprechen von negativem Wachstum oder auch Abnahme, wenn in gleichen Zeitabschnitten der neue Wert kleiner ist als der alte.
Berechnung: d = neue Größe - alte Größe bzw. durchschnittliches Wachstum: d = $\tfrac{Endwert-Anfangswert}{AnzahlderZeitabschnitte}$

Eine gleichmäßige Zunahme (bzw. Abnahme) heißt lineares Wachstum.

Beispiel: Lineares Wachstum
Eine Firma produziert jährlich 30000 Tischplatten. Nun sollen pro Jahr 2000 Platten mehr produziert werden. Wie viele Platten werden nach 5 Jahren gefertigt?
Anfangswert W₀ = 30000
Zunahme d = 2000
Anzahl der Zeitabschnitte n = 5
Rechnung:
W₅ = W₀ + n·d
     = 30000 + 5·2000
     = 3000 + 10000
     = 40000
Nach 5 Jahren werden 40000 Tischplatten jährlich produziert.

1 Lineares und exponentielles Wachstum

Sparmodell (vgl. Zinseszins) Erinnerung: Sparmodelle

1) Einstieg: Sparschwein

Sparschwein

Schreibe die Aufgabe und beide Möglichkeiten in dein Heft. Fülle die Tabelle aus.

Deine Oma schenkt dir zu deiner Geburt 1000€. Nun muss sie entscheiden, wie sie das Geld für dich angelegt. Die Bank bietet ihr einen Zinssatz von 5% an. Berechne, wie viel Geld du mit 18 Jahren bekämst. Übertrage die beiden Möglichkeiten in dein Heft und fülle die Tabelle aus.

1. Möglichkeit:
Sie lässt sich die Zinsen jedes Jahr auszahlen und spart sie in einem Sparschwein.

K = 1000€; p% = 5% = 0,05

Jahre	Guthaben(€)
0	1000
1	1050
2	1100
3	1150
...	...
18	...

2. Möglichkeit:
Sie lässt die Zinsen auf dem Sparbuch und fügt sie so jährlich dem Kapital zu.

K = 1000€; p% = 5% = 0,05

Jahre	Guthaben(€)
0	1000
1	1050
2	1102,50
3	1157,625
...	...
18	...

Beispielrechnung mit p% = 2% = 0,02

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Kannst du eine Formel angeben, mit der du den Endbetrag berechnen kannst?

Kapital nach 18 Jahren:
K₁₈ = ...

Kapital nach 18 Jahren:
K₁₈ = ...

Unterschiede zwischen einfacher Verzinsung und Zinseszins

Notiere Stichpunkte in deinem Heft, wie sich die einfache Verzinsung in der ersten Möglichkeit vom Zinsenzins der zweiten Möglichkeit unterscheidet. Nutze dazu auch nachfolgende Applet.
Stelle einen Wert für den Zinssatz p% mit dem Schieberegler ein. Dann ziehe den Schieberegler für die Zeit t und beobachte den Verlauf des Kapitals.
blau: einfache Verzinsung
rot: Zinseszins

Was fällt dir auf?

nach Pöchtrager

Lineares und exponentielles Wachstum

Lineares Wachstum:

W_n = W₀ + d·n

mit dem Anfangswert W₀ und der gleichmäßigen Zunahme bzw. Abnahme d.

Exponentielles Wachstum:

W_n = W₀ · qⁿ

mit dem Anfangswert W₀ und dem Wachstumsfaktor
q = 1 ± p%.

Bezogen auf die Zinsrechnung:

Hefteintrag: Zinseszins

Zinseszins bedeutet, dass ein Startkapital Zinsen erwirtschaftet und diese Zinsen werden dem Vermögen am Jahresende gutgeschrieben. So werden in Zukunft diese Zinsen ebenfalls verzinst.
Das Kapital nach n Jahren wird mit der Formel
K_n = K₀ ∙ (1+p%)ⁿ

      = K₀ ∙ qⁿ       mit q = 1+p%

Beispiel:
geg: K₀ = 1000€ (Startkapital, null Jahre); p% = 5% = 0,05; q = 1 + p% = 1 + 0,05 = 1,05; n = 18 Jahre
ges: K_n (Kapital nach n Jahren)

K₁₈ = 1000 ∙ 1,05¹⁸
      = 2406,62 (€)

Nach 18 Jahren ist das Kapital auf 2406,62 € angewachsen.

Du nutzt folgende Taste beim Taschenrechner, um Exponenten größer als 3 einzugeben (hier z.B. n = 18):

Das nachfolgende Video erklärt noch einmal den Zusammenhang zwischen p% und q.

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Bei diesem Kapitalwachstum handelt es sich um ein sogenanntes exponentielles Wachstum.

Übung 1: Lineares und exponentielles Wachstum

Unterscheide zwischen linearem und exponentiellem Wachstum. Bearbeitet dazu die nachfolgenden LearningApps.

2 Wachstumsrate und Wachstumsfaktor

Wachstumsrate und Wachstumsfaktor

Wird die Zunahme bzw. Abnahme in Prozent angegeben, heißt dieser Prozentsatz Wachstumsrate p%.
Beispiel: Das Kapital wächst pro Jahr um' 5%'. Die Wachstumsrate beträgt dann p% = 5%.
Das Kapital wächst also auf das 1,05-Fache.
Dies ist der Wachstumsfaktor q = 1,05. Er ergibt sich aus dem Grundwert von 100% und der Wachstumsrate p%:
q = 100% + p%
Das neue Kapital/den neuen Wert W₁ berechnest du also mit der Gleichung:
K₁ = K₀ · q oder

W₁ = W₀ · q

Beispiele
1) Die Schülerzahl einer Schule von 550 ist innerhalb eines Jahres um 8% gestiegen.
Geg: W₀ = 550; Wachstumsrate p% = 8%
Ges: W₁ ; q
Der alte Wert ist von 100% auf 108% gestiegen, also auf das 1,08-Fache.
Wachstumsfaktor q             q = 1 + p%    
           Die neue Größe ergibt sich aus dem Produkt der alten Größe mit dem Wachstumsfaktor q:
W₁ = W₀ ∙ q              
W₁= 550 ∙ 1,08
   = 594 (Schüler)
Die Anzahl der Schüler beträgt nun 594.

2) Die Anzahl der Schülerinnen und Schüler einer Schule stieg von 2017 bis 2018 von 540 auf 567. Bestimme die Wachstumsrate.
Geg: W₀ = 540; W₁ = 567
Ges: p% Wachstumsrate
Berechne die Wachstumsrate aus dem alten und neuen Wert:
Wachstumsrate:     p% = $\tfrac{W_1 - W_0}{W_0}$  = $\tfrac{567 - 540}{540}$ = 0,05 = 5%
Wachstumsfaktor: q = $\tfrac{W_1}{W_0}$  = $\tfrac{567}{540}$ = 1,05        (Formel W1 = W0 ∙ q nach q umgestellt)
oder q = 1 + 5% = 1 + 0,05 = 1,05           ( Probe: 440 ∙ 1,05 = 462)

IDEE LearningApp mit Anwendungsaufgaben zur Bestimmung von p% und q (noch erstellen!)

3 Exponentielles Wachstum

Einstieg: Weltbevölkerung

Im Jahr 2019 lebten 7,7 Mrd. Menschen auf der Erde. Wissenschaflter prognostizierten in diesem Jahr eine jährliche Zuwachsrate von 1,25%.
Also gilt q=100%+1,25% = 101,25% = 1,0125

Wie viele Menschen leben demnach im Jahr 2030 auf der Erde?

Stelle diese Situation auf verschiedene Arten dar. (Erinnerung: Text (ist gegeben), Wertetabelle, Funktionsgleichung und Funktionsgraph)

Datei:Weltbevölkerung Tipp Wertetabelle.png

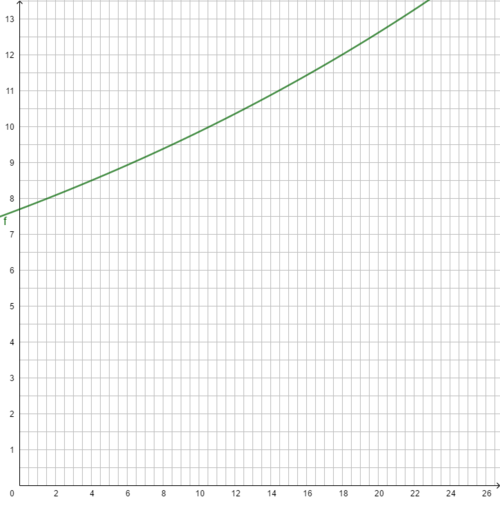
Prognose für das Jahr 2030: n = 11
W₁₁ = W₀ ∙ q¹¹
   = 7,70 ∙ 1,025¹¹

   ≈8,83

Exponentielles Wachstum - Exponentialgleichung

Wir sprechen von exponentiellem Wachstum, wenn der Wert einer Größe in gleichen Zeitspannen immer um denselben Prozentsatz p% zunimmt bzw. abnimmt.
Die neue Größe nach n Zeitspannen berechnen wir mit
W_n = W₀ · qⁿ,

wobei q der Wachstumsfaktor ist. q = 1+p% (Zunahmen) bzw.q=1-p%(Abnahme)

Die Gleichung W_n = W₀ · qⁿ heißt Exponentialgleichung, da die Variable n im Exponenten steht.

Anwendungsaufgabe 1: Erdbevölkerung

...(Anwendung, Wn gesucht)

Anwendungsaufgabe 2: Klimawandel

...(Anwendung W0 gesucht)

Exponentialgleichung - Formel umstellen

Anwendungsaufgabe 3

...(Anwendung q gesucht)

Anwendungsaufgabe 4

...(Anwendung n gesucht)

ÜBUNGSAUFGABEN ERGÄNZEN

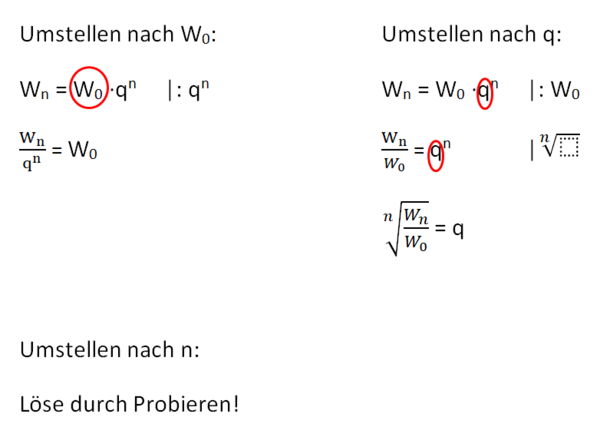
• Formel umstellen
• Verdopplungszeit (Bakterien)

Applet von Hegius, R. Schürz

• Halbwertszeit (Atome)

Applet von Hegius, R. Schürz

4 Die Exponentialfunktion

Exponentialfunktion

Die Funktion mit der Gleichung f(x) = c∙ax heißt Exponentialfunktion.

Eigenschaften der Exponentialfunktion

Beschreibe die Eigenschaften der Exponentialfunktion f(x) = c∙ax .

Wähle zunächst c=1. Wie verläuft der Graph der Funktion? Löse den Lückentext und übertrage ihn in dein Heft.

Applet von Ralf Wagner

Der Graph verläuft immer oberhalb der x-Achse.
Der Graph geht immer durch den Punkt (0|1).
Für a>1 steigt der Graph (Zunahme),

für 0<a<1 fällt der Graph (Abnahme).