Herta-Lebenstein-Realschule/Lernpfad Brüche

Im Aufbau Lernpfad zum Thema Brüche
	Brüche
In diesem Lernpfad wirst du durch die verschiedenen Rechenarten mit Brüchen geführt.

Wo stehe ich?
- Was ist ein Bruch?	Im Buch Seite 37 Nr. 1 und 2 und Seite 38 Nr. 7 und 8	https://www.mathe-lerntipps.de/was-ist-ein-bruch/
- Bruchteile von Größen	Bestimme den Bruchteil: $\frac{1}{3}$ von 180 mg https://www.realmath.de/Neues/Klasse6/bruchteil/groessbruch.html

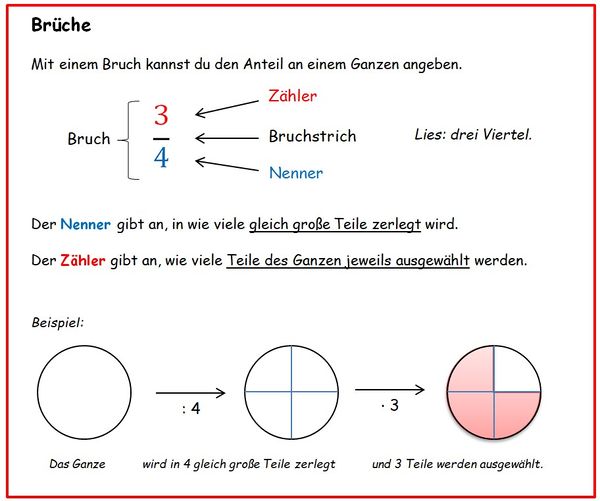
Einführung in das Thema Brüche

Merke: Brüche

Bruch als Division

Ein Bruch ist mit einer Division gleichzusetzen. Z.B.: $\frac{2}{3}$ = 2 : 3
Dabei gibt der Zähler die Anteile der Bruchteile an, in diesem Fall 2.
Der Bruchstrich steht für das Divisionszeichen

Der Nenner gibt an, in wie viele Teile das Ganze unterteilt ist, hier 3.

Bist du noch unsicher, schaue dir das folgende Video an.

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Aufgabe

Löse im Buch die Nr.: 3, 5, 6, 9 und 11 auf Seite 38

>Nr. 3
a) $\frac{2}{5}$
b) $\frac{3}{4}$
c) $\frac{2}{8}$
d) $\frac{5}{6}$
e) $\frac{7}{15}$
f) $\frac{3}{5}$

Nr. 5
a) $\frac{2}{6}$
b) $\frac{8}{12}$
c) $\frac{8}{15}$

Nr. 6
a) zu Fuß $\frac{11}{28}$
mit der Bahn $\frac{17}{28}$

b) weiße $\frac{10}{30}$
blaue $\frac{20}{30}$

c) Ananassaft: $\frac{1}{6}$
Apfelsaft: $\frac{2}{6}$
Orangensaft: $\frac{3}{6}$

Lösungen zu Nr. 9

Mach dir vor der Zeichnung des Rechtecks Gedanken über die Aufteilung. Der Nenner ist hierfür ausschlaggebend. Die Anzahl an Zentimetern oder Kästchen, die du wählst, sollte durch diese Zahl teilbar sein.

Aufgabe

Bearbeite im Folgenden die Aufgaben des folgenden Internetlinks https://www.alice.edu.tum.de/bruchrechnen.html#/10nks bis Seite 14 einschließlich

Verschiedene Brüche mit gleichem Wert

Aufgabe

Zeichne auf einem Blatt Papier ein Quadrat und schneide es aus. Markiere (Schraffiere) dann die Hälfte des Quadrates mit einer beliebigen Farbe. Besprich dich mit deinem Partner, wie ihr den entstandenen Bruch nun nennen würdet. Faltet das Quadrat nun weitere Male und besprecht, wie die entstandenen Brüche heißen.

Aufgabe

Lies dir die Seiten 30 - 34 im unten stehenden Link durch und bearbeite die entsprechenden Aufgaben

https://www.alice.edu.tum.de/bruchrechnen.html#/10nks

Merke

Notiere in deinem Heft.

Beim Erweitern eines Bruches werden Zähler und Nenner mit derselben Zahl multipliziert.

$\frac{3}{5}$=$\frac{3\cdot4}{5\cdot4}$=$\frac{12}{20}$

Bruch und erweiterter Bruch haben denselben Wert.

Beim Kürzen eines Bruches werden Zähler und Nenner durch dieselbe Zahl dividiert.

$\frac{15}{20} = \frac{15:5}{20:5} = \frac{3}{4}$

Bruch und gekürzter Bruch haben denselben Wert.

Bist du noch unsicher, schaue dir folgendes Video an.

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Aufgabe

Kontrolliere mit der folgenden App, ob du die Grundlagen verstanden hast. Spiele gegen deinen Partner. Wenn du keinen hast, spiele gegen den Computer. Mal sehen, wer das schnellere Pferd hat.

Aufgabe

Bearbeite im Folgenden die Aufgaben 4c, d, 5, 7c,d und 8 auf der Seite 43.

Nr. 4
c) $\frac{2}{100}$; $\frac{30}{100}$; $\frac{35}{100}$; $\frac{36}{100}$; $\frac{80}{100}$; $\frac{75}{100}$; $\frac{250}{100}$

d) $\frac{6}{1000}$; $\frac{44}{1000}$; $\frac{64}{1000}$; $\frac{48}{1000}$; $\frac{45}{1000}$

Nr. 5
a) $\frac{1}{2}$ = $\frac{6}{12}$

b) $\frac{4}{5}$ = $\frac{32}{40}$

c) $\frac{5}{9}$ = $\frac{35}{63}$

d) $\frac{3}{7}$ = $\frac{18}{42}$

e) $\frac{5}{9}$ = $\frac{60}{108}$

f) $\frac{8}{11}$ = $\frac{88}{121}$

g) $\frac{1}{3}$ = $\frac{9}{27}$

h) $\frac{2}{7}$ = $\frac{16}{56}$

i) $\frac{5}{8}$ = $\frac{45}{72}$

j) $\frac{7}{10}$ = $\frac{91}{130}$

k) $\frac{5}{12}$ = $\frac{60}{144}$

l) $\frac{9}{13}$ = $\frac{99}{143}$

Nr. 7

c) $\frac{1}{3}$; $\frac{2}{3}$; $\frac{3}{5}$; $\frac{4}{7}$; $\frac{5}{9}$

d) $\frac{2}{7}$; $\frac{4}{5}$; $\frac{3}{8}$; $\frac{7}{11}$; $\frac{9}{13}$

Nr. 8

a) mit 3; mit 2; mit 8

b) mit 5; mit 7; mit 8

Aufgabe

Festige dein Wissen, indem Du auf den untenstehenden Link klickst und die Aufgaben auf den Seiten 35 - 38 bearbeitest.

https://www.alice.edu.tum.de/bruchrechnen.html#/10nks

Aufgabe

Nehmt euch zu zweit drei Würfel und vollzieht die Aufgabe 10 im Buch S. 44 jeder dreimal und räumt dann die Würfel wieder zurück

Vollständiges Kürzen

Du kannst Brüche oft mehrmals kürzen.

$\frac{40}{80} = \frac{4}{8} = \frac{2}{4} = \frac{1}{2}$

Zuerst wurde der Bruch mit 10 gekürzt, dann mit 2 und letztlich nochmal mit 2. Um sofort mit dem größten gemeinsam Teiler zu kürzen, kannst Du auch die Teilermengen notieren (siehe grüner Kasten auf der Buchseite 44).

Bearbeite nun folgende Learningapps.

Aufgabe

Bearbeite die Aufgaben 12, 13 und 14 auf Seite 44.

Nr. 12
a) $\frac{42}{48}$ = $\frac{7}{8}$ (ggT: 6)

b) $\frac{90}{120}$ = $\frac{3}{4}$ (ggT: 30)

c) $\frac{54}{90}$ = $\frac{3}{5}$ (ggT: 18)

d) $\frac{40}{56}$ = $\frac{5}{7}$ (ggT: 8)

e) $\frac{72}{108}$ = $\frac{2}{3}$ (ggT: 36)

f) $\frac{60}{135}$ = $\frac{4}{9}$ (ggT: 15)

g) $\frac{48}{144}$ = $\frac{1}{3}$ (ggT: 48)

h) $\frac{54}{243}$ = $\frac{2}{9}$ (ggT: 27)

Nr. 13
a) gleich
b) gleich
c) ungleich
d) ungleich
e) ungleich
f) ungleich
g) ungleich

h) ungleich

Sucht zuerst den größten gemeinsamen Teiler.

Nr. 14
a) $\frac{8}{16}$ = $\frac{1}{2}$

b) $\frac{25}{75}$ = $\frac{1}{3}$

c) $\frac{12}{18}$ = $\frac{2}{3}$

d) $\frac{24}{64}$ = $\frac{3}{8}$

e) $\frac{36}{90}$ = $\frac{2}{5}$

f) $\frac{32}{128}$ = $\frac{1}{4}$

g) $\frac{48}{144}$ = $\frac{1}{3}$

h) $\frac{56}{140}$ = $\frac{2}{5}$

Vollständiges Kürzen

Vollständiges Kürzen

Lies dir im Buch den grünen Kasten auf Seite 44 durch und fülle dann den Lückentext unten aus. Übertrage ihn in dein Heft.

Brüche lassen sich häufig mehrmals kürzen.
$\frac{15}{45}$ = $\frac{5}{15}$ = $\frac{1}{3}$. Wie Du siehst gehören die Kürzungszahlen 3 und 5 zur Teilermenge des Zählers und Nenners. Stellst Du nun die Teilermenge auf, kannst Du sofort den größten gemeinsamen Teiler finden.
T₁₅ = {1; 3; 5; 15}
T₄₅ = {1; 3; 5; 15; 45} Also ist 15 der als ggT (größter gemeinsamer Teiler) zu bezeichnen. Folglich kannst Du auch sofort mit 15 kürzen:
$\frac{15}{45}$ = $\frac{1}{3}$

Der Bruch ist sofort vollständig gekürzt

Aufgabe

Bearbeite im Buch nun die Aufgabe 18 auf Seite 44.

Gemischte Zahlen

Aufgabe

Bearbeite im Buch die Einstiegsaufgabe oben auf Seite 39.

Es gibt zwei Möglichkeiten den Bruch darzustellen. Einmal als unechten Bruch und einmal als gemischte Zahl

Unechte Brüche und Gemischte Zahlen

Ein unechter Bruch ist gegeben, wenn der Zähler größer ist als der Nenner. Unechte Brüche kann man aber auch als gemsichte Zahl darstellen. Eine gemischte Zahl besteht aus einer natürlichen Zahl und einem Bruch.

Beispiel für einen unechten Bruch: $\frac{7}{3}$

Beispiel für eine gemischte Zahl: 2$\frac{1}{3}$

Schau Dir nun das folgene Video an.

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Aufgabe

Festige dein Wissen, indem du auf den untenstehenden Link klickst und die Aufgaben auf den Seiten 51 - 54 bearbeitest.

https://www.alice.edu.tum.de/bruchrechnen.html#/10nks

Aufgabe

Bearbeite nun die Aufgaben 1 und 2 auf Seite 39.

Aufgabe

Lies dir den Lerntipp auf der Seite 39 durch und erkläre ihn deinem Partner. Bearbeite im Anschluss die Aufgaben 3 und 4 auf der Seite. Du darfst rechnen wie im Beispiel oder aber wie Petra im Lerntipp

Aufgabe

Bearbeite Aufgabe 5 auf Seite 39

Wandle die gemischte Zahl zuerst in einen unechten Bruch um und ergänze dann die fehlende Zahl. Bei den Aufgaben d-f musst du zudem beachten, dass die Nenner auf beiden Seiten gleich sind.

Überprüfe dein Wissen abschließend mit den folgenden Learningapps.

Brüche am Zahlenstrahl

Notiere die Überschrift "Brüche am Zahlenstrahl"

Aufgabe

Öffne die Seite: https://www.alice.edu.tum.de/bruchrechnen.html#/40 und experimentiere mit den Animationen auf Seite 40. Lies dir die Seite 41 durch und schreibe den Merksatz in dein Heft.
Übernimm zudem die Skizze.

Bearbeite die Aufgaben bis zur Seite 43 einschließlich. Löse nun die Aufgaben 1-3 auf den Seiten 40 und 41 im Buch.

Wenn Du noch Probleme bei den Aufgaben hast, schau dir das folgende Video an:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Aufgabe

Bearbeite die Aufgaben bis zur Seite 47 des oben genannten Links einschließlich.
Übernimm den Merksatz auf Seite 47 in dein Heft. Nimm dir nun das Buch und schlage wieder die Seite 41 auf. Löse jetzt die Aufgaben
4a und 4c
5c und 5d sowie
6b und 6c

Überlege dir,wenn wie in Aufgabe a der ganze Zahlenstrahl 10 cm ist, wie groß ist dann ein Zehntel davon usw..

Mit dem Erweitern und Kürzen findest du die Lösungen.

Denke bei Aufgabe 6 daran, einen gemeinsamen Nenner aller Brüche zu finden, damit du eine passende Einteilung findest. Diese kannst du durch Kürzen/Erweitern finden.

Aufgabe

Bearbeite abschließend die Aufgaben 9-11 auf Seite 41 (mit deinem Partner).

Brüche ordnen und vergleichen

Aufgabe

Versuche dich an der Einstiegsaufgabe auf Seite 45. Wahrscheinlich wirst du nicht gleich auf die Lösung kommen. Wenn du Probleme hast, lies dir die untenstehenden Hinweise durch.

Beim Größenvergleich von Brüchen mit gleichem Nenner gehört zum größeren Zähler die größere Bruchzahl. Bei Brüchen mit verschiedenen Nennern ist es meist notwendig, sie zum Vergleichen zuerst auf gleiche Nenner zu bringen.

Beispiele: Wir ordnen der Größe nach: $\frac{7}{9}$; $\frac{4}{9}$; $\frac{13}{9}$ .
Da die Brüche gleichnamig sind und 4 < 7 < 13 ist, gilt $\frac{4}{9}$ < $\frac{7}{9}$ < $\frac{13}{9}$.

b) Um $\frac{5}{8}$ und $\frac{3}{9}$ zu vergleichen, müsen die Brüche durch erweitern gleichnamig gemacht werden. Gleichnamig bedeutet, dass der Nenner bei beiden Brüchen gleich ist. $\frac{5}{8}$ = $\frac{45}{72}$ und $\frac{3}{9}$ = $\frac{24}{72}$
Da $\frac{24}{72}$ < $\frac{45}{72}$, gilt $\frac{3}{9}$ < $\frac{5}{8}$

Aufgabe

Bearbeite auf der Internetseite:https://www.alice.edu.tum.de/bruchrechnen.html#/57 die Aufgaben ab Seite 56 - 63. Notiere den Merksatz in dein Heft. Bearbeite nun die Aufgabe 1a und 1b auf Seite 46 im Buch. Arbeite weiter auf der Internetseite: Seiten 64 - 66. Bearbeite nun die Aufgaben 1c und 9 auf Seite 46

https://www.alice.edu.tum.de/bruchrechnen.html#/10nks

Suche immer den gemeinsamen Nenner und erweitere oben (Zähler) mit derselben Zahl wie unten (Nenner).

Wenn ihr Probleme bei der Bearbeitung habt, schaut euch nochmal das folgende Video an.

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Aufgabe

Bearbeite die Aufgaben 2 und 5 auf der Buchseite 46 .

Denke bei Aufgabe 2a an echte und unechte Brüche. Echte Brüche sind kleiner als 1, unechte größer. Bei 2b musst du schauen, ob der Zähler, weniger als die Hälfte des Nenners hat, dann ist der Bruch kleiner als $\frac{1}{2}$, ist der Zähler genau die Hälfte des Nenners ist es genau $\frac{1}{2}$ und ist der Zähler größer als die Hälfte des Nenners, ist der Bruch größer als $\frac{1}{2}$. Bei 2c musst du nur die Brüche finden, deren Zähler größer als die Hälfte des Nenners sind.

Suche immer den gemeinsamen Nenner und erweitere oben (Zähler) mit derselben Zahl wie unten (Nenner).

Aufgabe

Bearbeite die Aufgaben 7 und 8 auf Buchseite 46 im Heft.

Prozent

Aufgabe

Die Klasse 8a hat insgesamt 28 Schüler. Die Hälfte der Klasse spielt Fußball. 25 % der Klasse sind dem Reitsport verpflichtet und die übrigen betreiben gar keine Sportart. Wie viele Schüler spielen Fußball und wie viel Prozent sind das? Wie viele Schüler reiten und wie viel Prozent sind das?

Wie sieht das für die Nichtsportler aus?

28 Schüler ergeben einhundert Prozent. Die Hälfte sind 25%. 25 ist die Hälfte von 50%

Prozentrechnung im Alltag

Wir schenken euch die Mehrwertssteuer von 19%.
Alle T-shirts um 20 % reduziert.
50% der Klasse hat eine drei oder besser geschrieben.
Der Pullover besteht zu 40 Prozent aus Seide und 60% aus Baumwolle.

Ihr seht, dass die Prozentrechnung häufig Verwendung findet. Sicher ist euch der Begriff auch schon begegnet.

Prozent

Aber was bedeutet Prozent überhaupt. Prozent ist aus dem Lateinischen (pro centum) und hat die Bedeutung von Hundert oder Hundertstel. 50% bedeutet also 50 von Hundert: $\frac{50}{100}$
6% bedeutet also 6 von Hundert: $\frac{6}{100}$
Möchte ich nun einen Bruch in Prozent umwandelt, mache ich das folgendermaßen: $\frac{24}{25}$ = $\frac{96}{100}$ = 96%

Ich habe also den Nenner auf Hundert gebracht und den Zähler ebenfalls mit 4 multipliziert, so dass ich nun die Prozentzahl von 96 im Zähler ablesen kann.

Schau dir das folgende Video zur Verdeutlichung an.

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Schreibe nun den Satz in dem gelben Kasten auf Seite 47 ab und den Lerntipp auf Seite 48.

Versucht nun die Aufgaben in den Learninapps zu lösen.

Aufgabe

Bearbeitet nun die Aufgaben 1 und 2g-l auf Seite 47

Bringe den Nenner, falls nötig, immer zuerst auf einhundert und multipliziere den Zähler mit der selben Zahl wie dem Nenner. Nun kannst Du im Zähler die Prozentzahl ablesen.

Tipp zu Nr. 2

Aufgabe

Bearbeitet nun die Aufgabe 4a-f und die Aufgabe 5 auf Seite 48.

Bearbeitet nun folgende learningapp.

Aufgabe

Bearbeitet nun die Aufgaben 7 und 10 auf Seite 48

Zähle zuerst alle Kästchen (Nenner) und dann die markierten (Zähler) und stelle den Bruch auf. Bringe den Nenner auf hundert und multipliziere den Zähler mit der selben Zahl wie den Nenner. Der Zähler gibt nun die Prozentzahl an.

Applet zur Addition gleichnamiger Brüche:

und nun die Subtraktion:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Applet zur Addition ungleichnamiger Brüche

Übe mit dem folgenden Link die Addition und Subtraktion von Brüchen: Matheaufgabennet Bruchrechnung

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden