Benutzer:Buss-Haskert/Quadratische Funktionen/Nullstellen: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
K (Einstiegsaufgabe formuliert)
Markierung: 2017-Quelltext-Bearbeitung
KKeine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Zeile 5: Zeile 5:
Eine Parabel habt ihr in der Form der Reichstagskuppel gefunden. Nun können wir verschiedene Fragen an dieses Bild stellen.
Eine Parabel habt ihr in der Form der Reichstagskuppel gefunden. Nun können wir verschiedene Fragen an dieses Bild stellen.


{{Box|Einstieg: Anwendung Reichstag|Die Funktionsgleichung der Parabel lautet f(x) = -0,059x² + 23,5.
{{Box|1=Einstieg: Anwendung Reichstag|2=Die Funktionsgleichung der Parabel lautet f(x) = -0,05875x² + 23,5.
* Welche Form hat diese Parabelgleichung und warum?
* Welche Form hat diese Parabelgleichung und warum?
* Stellt verschiedene Fragen an das Foto, die mithilfe der Parabelgleichung beantwortet werden können.|Frage}}
* Stellt verschiedene Fragen an das Foto, die mithilfe der Parabelgleichung beantwortet werden können.|3=Frage}}


[[Datei:Bild Reichstag mit Koordinatenkreuz.png|rahmenlos|500x500px]]
[[Datei:Bild Reichstag mit Koordinatenkreuz.png|rahmenlos|500x500px]]
Zeile 21: Zeile 21:


Um die Frage nach dem Durchmesser des Kuppeldaches zu beantworten, müssen wir herausfinden, wo die Parabel die x-Achse schneidet.
Um die Frage nach dem Durchmesser des Kuppeldaches zu beantworten, müssen wir herausfinden, wo die Parabel die x-Achse schneidet.
Diese besonderen Stellen heißen Nullstellen der Funktion.
Diese besonderen Stellen heißen '''Nullstellen''' der Funktion.
 
 
{{Box|Nullstellen quadratischer Funktionen|Die Schnittpunkte einer Funktion mit der x-Achse heißen '''Nullstellen''',<br>
denn y-Koordinate dieser Punkte hat immer den Wert Null. N(x<sub>N</sub>&#124;'''0''')|Kurzinfo}}
 
=== 7.1 Anzahl der Nullstellen quadratischer Funktionen erkennen ===
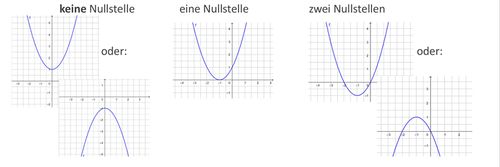
Ist die Parabelgleichung in der Scheitelpunktform gegeben, kannst du die Anzahl der Nullstellen erkennen. <br> Je nach Lage des Scheitelpunktes und der Öffnung der Parabel hat diese keine, eine oder zwei Nullstellen:<br>
[[Datei:Anzahl der Nullstellen .jpg|ohne|mini|500x500px]]<br>
 
ÜBUNG (noch ergänzen)
 
=== 7.2 Nullstellen berechnen ===
 
Um den Durchmesser der Reichstagskuppel zu berechnen, müssen wir die Nullstellen der Funktion f(x) = -0,05875x² + 23,5 berechnen.<br>
Da die y-Koordinate der Nullstellen immer 0 ist, setzen wir dies in die Gleichung ein:<br>
 
f(x) '''= 0'''<br>
 
-0,05875x² + 23,5 = 0 &nbsp;&nbsp;&#124;-23,5<br>
-0,05875x² = -23,5 &nbsp;&nbsp;&#124;:(-0,059)<br>
x² = 400 &nbsp;&nbsp;&#124;<math>\pm\surd</math><br>
x = <math>\pm</math>20<br>
 
Die Nullstellen lauten also N<sub>1</sub>(-20&#124;0) und N<sub>2</sub>(20&#124;0).<br>
Der Durchmesser der Kuppel beträgt also 20m+20m = 40m.
 
 
 
 
 
 
Löse diese Gleichung nach x auf.
 
 




Version vom 29. September 2021, 17:17 Uhr

7 Nullstellen quadratischer Funktionen

Ihr wart zur Klassenfahrt in Berlin und habt dort verschiedene Parabeln entdeckt.

Eine Parabel habt ihr in der Form der Reichstagskuppel gefunden. Nun können wir verschiedene Fragen an dieses Bild stellen.


Einstieg: Anwendung Reichstag

Die Funktionsgleichung der Parabel lautet f(x) = -0,05875x² + 23,5.

  • Welche Form hat diese Parabelgleichung und warum?
  • Stellt verschiedene Fragen an das Foto, die mithilfe der Parabelgleichung beantwortet werden können.

Bild Reichstag mit Koordinatenkreuz.png

Die Form der Parabelgleichung ist f(x) = ax² + c. Passen die Zahlen für a und c zum Bild?

Die Form der Parabelgleichung ist f(x) = ax² + c.
Diese Parabel ist also symmetrisch zur y-Achse. Der Parameter a muss negativ sein, denn die Parabel ist nach unten geöffnet. Zudem muss -1<a<0 sein, denn die Parabel ist gestaucht.

Der Parameter c muss positiv sein, denn der Scheitelpunkt ist entlang der y-Achse nach oben verschoben.

Fragen:

  • Wie hoch reicht das Kuppeldach über das Dach des Reichstags?
  • Wie groß ist der Durchmesser der Kuppel?
  • ...

Um die Frage nach dem Durchmesser des Kuppeldaches zu beantworten, müssen wir herausfinden, wo die Parabel die x-Achse schneidet. Diese besonderen Stellen heißen Nullstellen der Funktion.


Nullstellen quadratischer Funktionen

Die Schnittpunkte einer Funktion mit der x-Achse heißen Nullstellen,

denn y-Koordinate dieser Punkte hat immer den Wert Null. N(xN|0)

7.1 Anzahl der Nullstellen quadratischer Funktionen erkennen

Ist die Parabelgleichung in der Scheitelpunktform gegeben, kannst du die Anzahl der Nullstellen erkennen.
Je nach Lage des Scheitelpunktes und der Öffnung der Parabel hat diese keine, eine oder zwei Nullstellen:

Anzahl der Nullstellen .jpg


ÜBUNG (noch ergänzen)

7.2 Nullstellen berechnen

Um den Durchmesser der Reichstagskuppel zu berechnen, müssen wir die Nullstellen der Funktion f(x) = -0,05875x² + 23,5 berechnen.
Da die y-Koordinate der Nullstellen immer 0 ist, setzen wir dies in die Gleichung ein:

f(x) = 0

-0,05875x² + 23,5 = 0   |-23,5
-0,05875x² = -23,5   |:(-0,059)
x² = 400   |
x = 20

Die Nullstellen lauten also N1(-20|0) und N2(20|0).
Der Durchmesser der Kuppel beträgt also 20m+20m = 40m.




Löse diese Gleichung nach x auf.



IDEENSAMMLUNG Modellieren Aufgabe Basektball (mit Lösungsschritten)

Abgerufen von „https://projekte.zum.de/index.php?title=Benutzer:Buss-Haskert/Quadratische_Funktionen/Nullstellen&oldid=52338“