|
|
| Zeile 1: |
Zeile 1: |
| SEITE IM AUFBAU | | SEITE IM AUFBAU |
|
| |
|
| [[Datei:Duisburg-Friedrich-Ebert-Brücke.jpg|rahmenlos]] [[Datei:Essen Grugapark Wasserfontäne.jpg|rahmenlos]] [[Datei:EVD-saltolargo-145.jpg|rahmenlos]] | | [[Datei:Duisburg-Friedrich-Ebert-Brücke.jpg|rahmenlos|© Raimond Spekking / CC BY-SA 4.0 (via Wikimedia Commons)]] [[Datei:Essen Grugapark Wasserfontäne.jpg|rahmenlos]] [[Datei:EVD-saltolargo-145.jpg|rahmenlos]] |
|
| |
|
| {{Box|Quadratische Funktionen und Gleichungen|In diesem Lernpfad zu quadratischen Funktionen und Gleichungen lernst du | | {{Box|Quadratische Funktionen und Gleichungen|In diesem Lernpfad zu quadratischen Funktionen und Gleichungen lernst du |
SEITE IM AUFBAU



Quadratische Funktionen und Gleichungen
In diesem Lernpfad zu quadratischen Funktionen und Gleichungen lernst du
- Was eine quadratische Funktion und eine quadratische Gleichung ist,
- dass die Graphen quadratischer Funktionen Parabeln sind,
- welche Parameter der Funktionsgleichung für die Form und Lage der Parabel verantwortlich sind,
- wie du Nullstellen quadratischer Funktionen berechnest,
- mit quadratischen Funktionen und Gleichungen zu modellieren.
Die Aufgaben beziehen sich auf das Buch "Schnittpunkt Mathematik - Differenzierende Ausgabe" des Klett-Verlages
Mathematik im Sportunterricht
Wähle eine Wurf-bzw. Stoßbewegung aus und beantworte die nachfolgenden Fragen.
- Weitwurf
- Kugelstoßen
- Weitsprung
- Basketball-Korbwurf
Beobachte jeweils die Flugkurve des Balls/der Kugel/der springenden Person und skizziere diese im Heft.
Welche Bedeutung haben die Koordinatenachsen? Beschrifte!
Stelle Fragen, die mithilfe der gezeichneten Kurve beantwortet werden können.
Mögliche Fragen könnten sein:
- In welcher Höhe wird der Ball abgeworfen?
- Wie hoch fliegt der Ball maximal?
- Wie weit fliegt der Ball?
| Frage
|
Mathematik
|
| In welcher Höhe wird der Ball abgeworfen?
|
Schnittpunkt mit der y-Achse, y-Achsenabschnitt
x = 0
|
| Wie hoch fliegt der Ball maximal?
|
Scheitelpunkt S (d|e)
|
| Wie weit fliegt der Ball?
|
Nullstelle
y = 0
|
||
Die Flugkurven haben alle eine Gemeinsamkeit. Ihre Form nennt man Parabel. Sie sind die Graphen/Schaubilder quadratischer Funktionen.
(auch als kahoot!)
Übung 1 (HA)
Suche parabelförmige Bögen in deiner Umgebung. Fotografiere mindestens eine Parabel, notiere, wo du sie entdeckt hast und wie sie aussieht (z.B. breit, schmal, nach oben oder nach unten geöffnet). Lade das Foto im Gruppenordner Mathematik hoch.
Übung 2 Parabel und Gleichung
- Skizziere die Flugkuren/Bögen aus den Applets in dein Heft.
- Notiere die passende Funktionsgleichung.
- Notiere Gemeinsamkeiten und Unterschiede der Flugkurven und Funktionsgleichungen.
Beispiel 1:
Link zum Applet (falls es nicht vollständig dargestellt wird): [1]
Applet von C. Buß-Haskert
Beispiel 2:
Link zum Applet (falls es nicht vollständig dargestellt wird): [2]
Applet von C. Buß-Haskert
Beispiel 3:
Link zum Applet (falls es nicht vollständig dargestellt wird): [3]
Applet von C. Buß-Haskert
Link zum Applet (falls es nicht vollständig dargestellt wird): [4]
Applet von Bobby Knurek
Link zum Applet (falls es nicht vollständig dargestellt wird):[5] br>
Applet von Luc Morth
Link zum Applet (falls es nicht vollständig dargestellt wird):[6]
Applet von G.von Lechberg
Ergebnis: Quadratische Funktionen
Die Funktionsgleichungen quadratischer Funktionen haben immer die Form
f(x) = a(x+d)² + e (Scheitelpunktform) bzw. f(x) = ax² + bx + c (allgemeine Form).
Nun gilt es, die Bedeutung der Parameter a, d und e bzw. b und c zu erarbeiten!
Dazu beginnen wir mit der einfachsten Form der quadratischen Funktion, nämlich für a=1; d=0 und e=0 bzw. b=0 und c=0.
Diese Gleichung lautet f(x) = x².
Die Normalparabel
Die Normalparabel
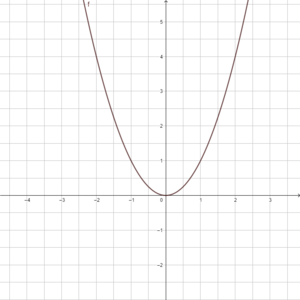
Die einfachste Form der quadratischen Funktionen lautet f(x) = x².
Der Graph der quadratischen Funktion f(x) = x² heißt Normalparabel.
Erstelle eine Wertetabelle und zeichne die Normalparabel in dein Heft.
| x
|
-2
|
-1
|
-0,5
|
0
|
0,5
|
1
|
2
|
| f(x)=x²
|
4
|
...
|
...
|
...
|
...
|
...
|
...
|
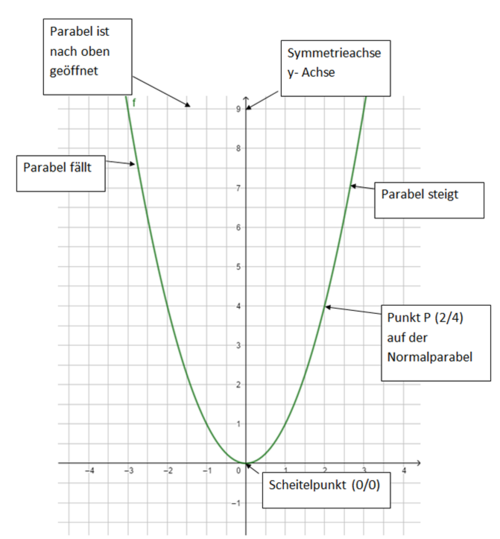
Beschreibe die Parabel:
- Wie verläuft der Graph im Koordinatensystem?
- Wie ist die Lage des Graphen im Koordiantensystem?
- Welche Form hat der Graph?
Erinnerung: (-2)² = (-2)·(-2) = +4
(Falls du später den Taschenrechner benutzt, denke an die Klammer, falls die Zahl ein Minuszeichen als Vorzeichen hat.)
Fülle den Lückentext aus.
Vergleiche deine Lösung:
Übung 3:Punkte auf der Normalparabel
Du hast eine Wertetabelle für die Normalparabel erstellt und diese gezeichnet. Prüfe nun zeichnerisch und rechnerisch, welche Punkte auf der Normalparabel liegen bzw. bestimme die fehlende Koordinate.
- S. 11 Nr. 6 (Tipps unten!, Beispiel)
- S. 11 Nr. 5
- S. 11 Nr. 7
Du kannst mithilfe des Schaubildes (Normalparabel) entscheiden, welche Punkte auf der Normalparabel liegen und welche nicht:
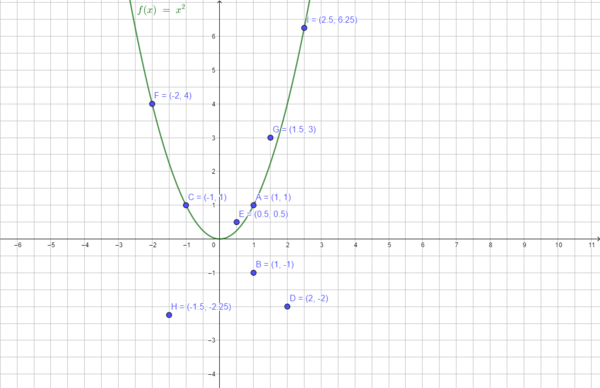
Wie kannst du rechnerisch prüfen, ob ein Punkt auf der Normalparabel liegt oder nicht?
Liegt ein Punkt auf der Parabel? - Punktprobe
Um zu prüfen, ob ein Punkt auf der Parabel liegt, setze in die Funktionsgleichung die Werte der Koordinaten für x und y ein.
Ergibt sich eine wahre Aussage (w), liegt der Punkt auf der Parabel, entsteht eine falsche Aussage (f), so liegt der Punkt nicht auf der Parabel.
Beispiel:
Liegt der Punkt I(2,5|6,25) auf der Normalparabel?
f(x) = x²
6,25 = 2,5²
6,25 = 6,25 (w), also liegt der Punkt I auf der Normalparabel.
Liegt der Punkt H(-1,5|-2,25) auf der Normalparabel?
f(x) = x²
-2,25 = (-1,5)²
-2,25 = 2,25 (f), also liegt der Punkt H nicht auf der Normalparabel.
Fehlende Koordinate bestimmen
Um eine fehlende Koordinate zu bestimmen, setze die gegebene Koordinate passend in die Funktionsgleichung ein und löse die Gleichung nach der fehlenden Koordinate auf.
Beispiel:
Bestimme die fehlende Koordinate von P(6|__) auf der Normalparabel.
f(x) = x²
y = 6²
y = 36, also P(6|36)
Bestimme die fehlende Koordinate von Q(__|1,69) auf der Normalparabel.
f(x) = x²
1,69 = x² |
 = x
= x
1,3 = x1; -1,3 = x2, also lautet Q1(1,3|1,69) und Q2(-1,3|1,69).
Es gibt zwei Punkte, die den y-Wert 1,69 haben, denn die Normalparabel ist symmetrisch zur y-Achse.
Die gestreckte und gestauchte Parabel: Bedeutung des Parameters a in f(x) = ax²
Link zum Applet (falls es nicht vollständig dargestellt wird):[7]
Applet von G.von Lechberg
f(x) = ax² Bedeutung des Parameters a
Untersuche die Bedeutung des Parameters a in der Gleichung f(x) = ax² mithilfe der Geometriesoftware GeoGebra.
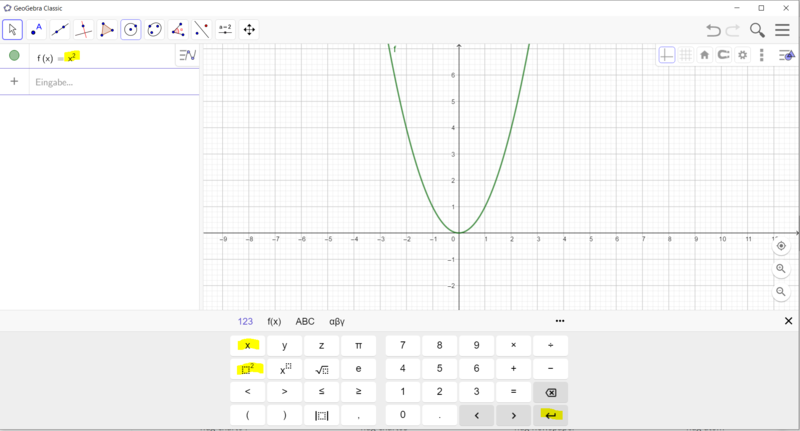
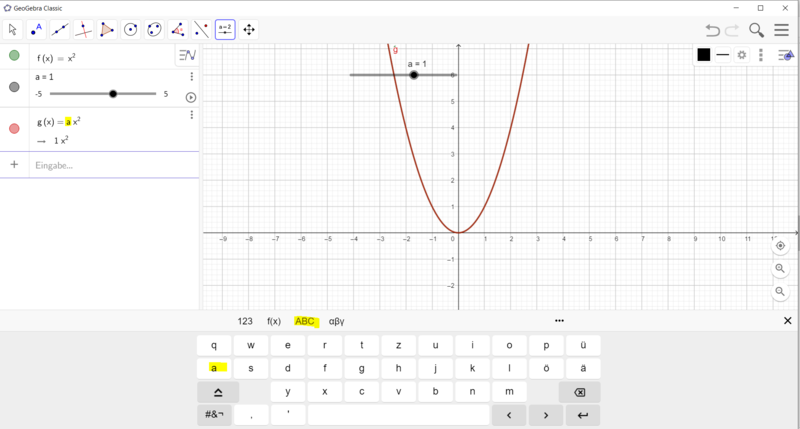
- Gib im Algebrafenster die Gleichung f(x) = x² ein. Es wird die Normalparabel gezeichnet.
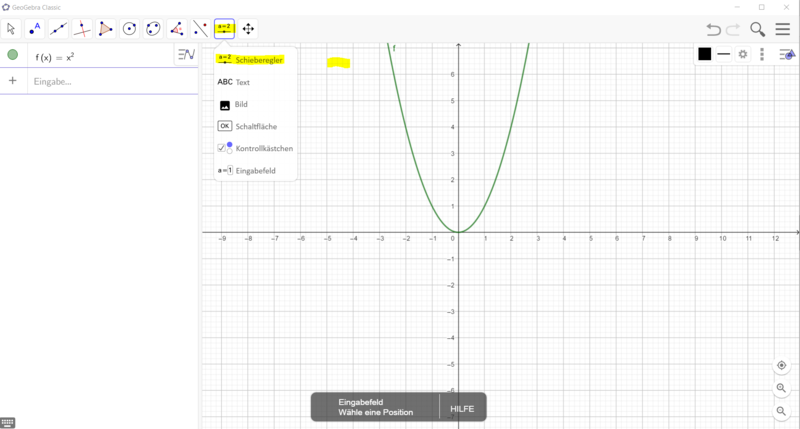
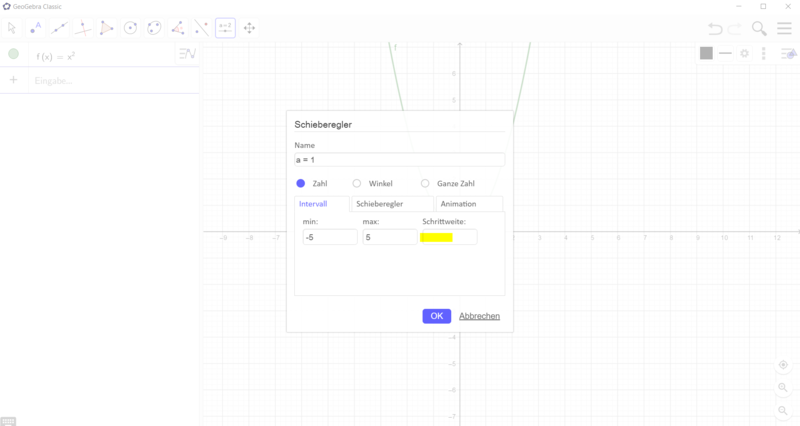
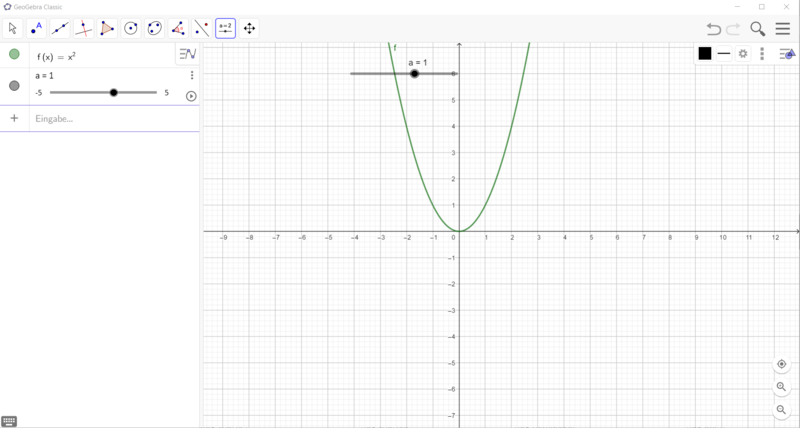
- Erstelle einen Schieberegler a mit der Schrittweite 0,1.
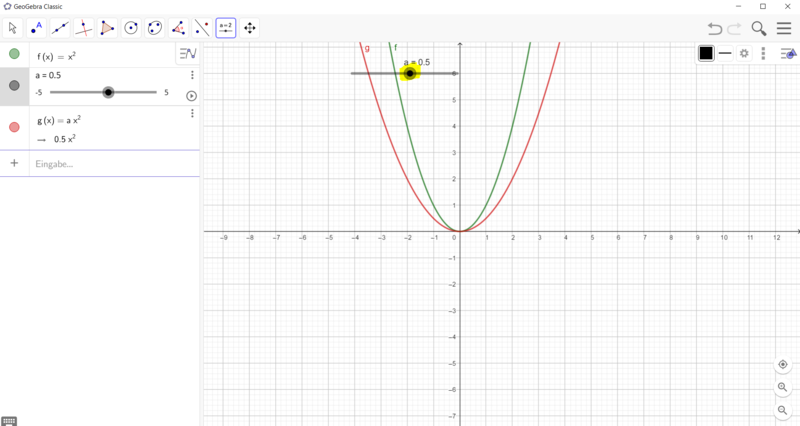
- Gib im Algebrafenster die Gleichung f(x) = ax² ein. Verändere den Wert von a mithilfe des Schiebereglers.
- Wie verändert sich die Parabel? Notiere deine Beobachtungen.
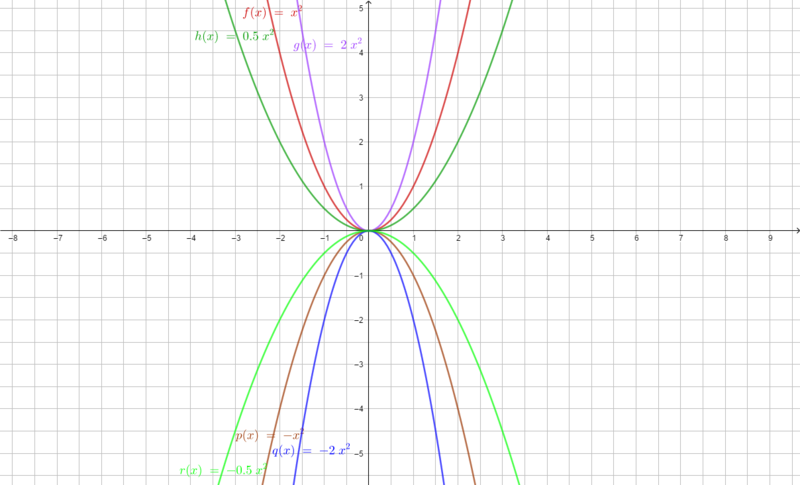
f(x) = ax² Bedeutung des Parameters a
Erstelle nun eine Wertetabelle zu den verschiedenen Funktionsgleichungen und zeichne die Parabeln in ein Koordinatenkreuz in dein Heft. Notiere die Bedeutung des Parameters a für den Verlauf der Parabel.
| x
|
-2
|
-1
|
-0,5
|
0
|
0,5
|
1
|
2
|
Öffnung
|
Form
|
| f(x) = x²
|
4
|
1
|
0,25
|
0
|
...
|
...
|
...
|
nach oben
|
Normalparabel
|
| f(x) = 2x²
|
8
|
2
|
0,5
|
0
|
...
|
...
|
...
|
nach oben
|
gestreckt
|
f(x) =  x² x²
|
2
|
0,5
|
...
|
...
|
...
|
...
|
...
|
...
|
gestaucht
|
| f(x) = -x²
|
-4
|
...
|
...
|
...
|
...
|
...
|
...
|
...
|
...
|
| f(x) = -2x²
|
-8
|
...
|
...
|
...
|
...
|
...
|
...
|
...
|
...
|
f(x) = - x² x²
|
-2
|
...
|
...
|
...
|
...
|
...
|
...
|
...
|
...
|
Verwende verschiedene Farben.
Vergleiche deine Lösungen
Die Parameter sportlich erarbeiten
Bearbeite im
Lernpfad das Kapitel zu
anton.