Benutzer:Buss-Haskert/Buss-Haskert/Körper/Pyramide: Unterschied zwischen den Versionen
Benutzer:Buss-Haskert/Körper>Buss-Haskert KKeine Bearbeitungszusammenfassung |
K (1 Version importiert: Umbenennung mit Benutzer...) |
Aktuelle Version vom 25. April 2021, 06:09 Uhr
Teile dieser Seite sind dem Lernpfad von Christine Staudermann auf der Seite der ZUM-Unterrichten entnommen [1]. Diese Seite wurde erstellt unter der CC BY SA Linzenz. Herzlichen Dank!
1) Pyramide
1) Merkmale einer Pyramide
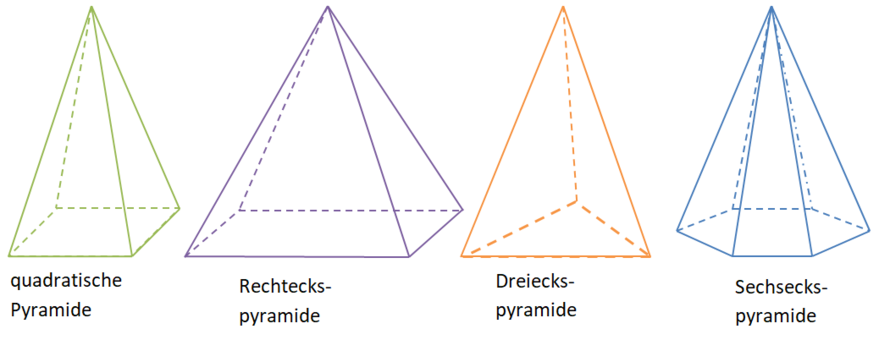
Eine Pyramide ist ein Spitzkörper. Die Grundfläche ist ein n-Eck (z.B. Dreieck, Quadrat, Rechteck, Fünfeck,...). Dieses bestimmt den Pyramidentyp: Dreieckspyramide, quadratische Pyramide, Fünfeckspyramide,...
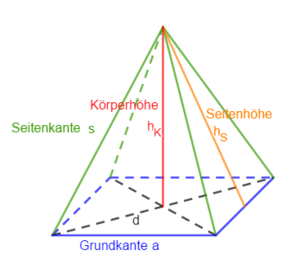
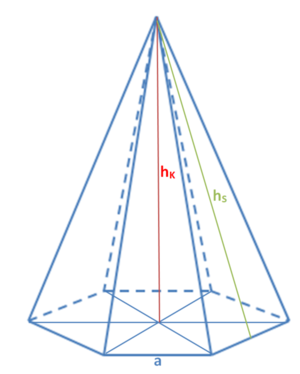
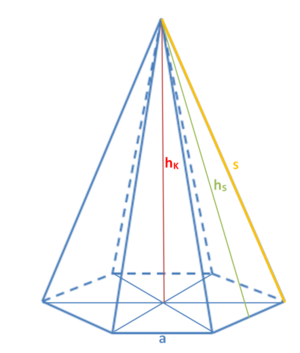
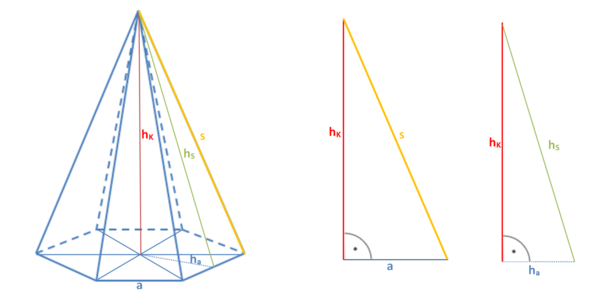
Der Abstand der Spitze von der Grundfläche heißt Höhe hK der Pyramide.
Die Seiten zwischen Pyramidenspitze S und Ecken der Grundfläche nennt man Seitenkanten s.
Die Seiten der Grundfläche werden auch Grundkanten a genannt. Die Seitenflächen einer Pyramide sind immer Dreiecke und bilden zusammen die Mantelfläche.
Hier siehst du die Bezeichnungen an einer quadratischen Pyramide:
Pyramiden können also jedes beliebige n-Eck als Grundfläche haben. Es gibt genauso viele der Seitenflächen wie die Grundfläche Ecken hat!
Im nachfolgenden GeoGebra-Applet kannst du die Anzahl der Ecken der Grundfläche (regelmäßiges n-Eck) einstellen. Dir wird dann die dazugehörige Pyramide im Schrägbild gezeichnet. Du kannst die Kantenlänge der Grundfläche ändern, indem du den Punkt B verschiebst und die Höhe der Pyramide, indem du Punkt J verschiebst.

Pyramiden können sich aber nicht nur in ihrer Grundfläche und somit in der Anzahl der Seitenflächen unterscheiden. Man differenziert auch zwischen geraden (bzw. senkrechten) und schiefen Pyramiden.
Betrachte dazu auch das GeoGebra Applet "Gerade und schiefe Pyramide" .

(von T. Weis)
1. Wie viele Ecken hat eine dreiseitige Pyramide? (!3) (!5) (4)
2. Wie viele Kanten hat eine sechsseitige Pyramide? (!6) (!14) (!10) (12)
3. Wie viele Flächen hat eine quadratische Pyramide? (!4) (!6) (5)
In diesem Lernpfad werden wir ausschließlich gerade Pyramiden mit 3-, 4- oder 6-seitiger Grundfläche berechnen (Dreieckspyramide, quadratische Pyramide und Sechseckspyramide).
2) Schrägbild und Netz einer Pyramide
Das nachfolgende Applet zeigt das Schrägbild einer quadratischen Pyramide. Du kannst die Länge der Grundkanten und die Höhe der Pyramide mit den Schiebereglern verändern.

Applet von Markus Böckler
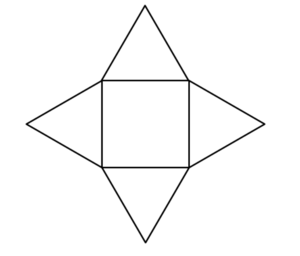
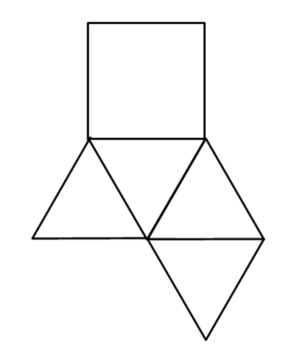
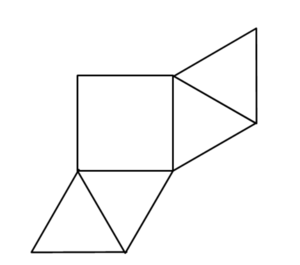
Die Netze einer Pyramide können verschieden aussehen. Hier siehst du einige Beispiele:
In den Applets kannst du die Pyramiden jeweils zu deren Netz entfalten. Schiebe am Regler.


(LearningApp von Jola)
3) Oberfläche einer Pyramide
Die Oberfläche einer Pyramide setzt sich zusammen aus der Grundfläche G und der Mantelfläche M.
Die Mantelfläche besteht aus so vielen gleichschenkligen Dreiecken, wie die Grundfläche Ecken hat.
Formel: O = G + M.
Die Grundfläche G ist ein Quadrat mit der Kantenlänge a. G = AQuadrat=a²
Die Mantelfläche M setzt sich zusammen aus 4 gleichschenkligen Dreiecken. ADreieck=∙g∙hDreieck
Setze ein:
o = G + M
Hefteintrag (nach der Herleitung der Formel):

Umstellen der Mantelformel nach a:
M = 2∙a∙hS |:2
= a∙hS |:hS
Umstellen der Mantelformel nach hS:
M = 2∙a∙hS |:2
= a∙hS |:a
Hilfsdreiecke in der Pyramide
Für Berechnungen an Pyramiden benötigt man die Maße der Pyramidengrundfläche und der Körperhöhe hK und die Höhe der Seitenfläche hS. Diese sind allerdings nicht immer direkt gegeben und müssen erst aus den angegebenen Seitenlängen berechnet werden.
Hier nutzen wir Hilfsdreiecke. Bei den Hilfsdreiecken handelt es sich um rechtwinklige Dreiecke, wobei bereits zwei der Seiten gegeben sind. Die dritte Seite lässt sich dann durch Anwendung des Satzes von Pythagoras berechnen!

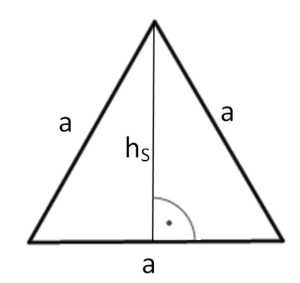
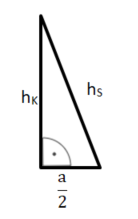
Hilfsdreieck 1: halber Parallelschnitt
Die Katheten in diesem rechtwinkligen Dreieck sind die halbe Grundseite und die Höhe der Pyramide hK. Die Hypotenuse ist die Höhe der Seitenfläche hS.
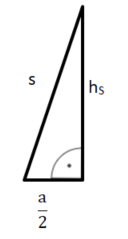
Hilfsdreieck 2: halber Seitenfläche
Die Katheten in diesem rechtwinkligen Dreieck sind die halbe Grundseite und die Höhe der Seitenfläche hS. Die Hypotenuse ist die Seitenkante s .
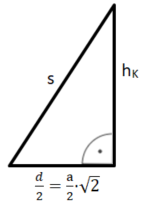
Hilfsdreieck 3: halber Diagonalschnitt
Die Katheten in diesem rechtwinkligen Dreieck sind die halbe Diagonale der Grundseite und die Höhe der Pyramide hK. Die Hypotenuse ist die Seitenkante s .
Umstellen der Mantelformel nach a:
M = 2∙a∙hS |:2
= a∙hS |:hS
Umstellen der Mantelformel nach hS:
M = 2∙a∙hS |:2
= a∙hS |:a
Berechne die Grundfläche G=a². Dann kannst du M=O-G ausrechnen.
Stelle dann die Formel für M nach hS um.
...
hS18,4 cm
Um h und s zu berechnen wähle passende Teildreiecke.
Berechne die Grundfläche G mit O - M = G. Dann kannst du a bestimmen, denn G=a².
a=10 cm
Stelle dann die Formel für M nach hS um.
...
hS11,7 cm
Um s zu berechnen wähle ein passendes Teildreieck.
Berechne mit dem Teildreieck 3"halbe Seitenfläche" die Höhe hS. Lösung: 6,5 cm
Nun kannst du die Oberfläche berechnen. Lösung:O 153,75 cm².
Zeichne eine Skizze und beschrifte sie mit den Angaben aus der Aufgabe. Da das Parallelschnitt-Dreieck ein rechtwinklig gleichschenkliges Dreieck ist, sind die Katheten die Höhen der Seitenflächen hS.
Hier gilt also hS = 12,8 cm.
geg: O=470m²;hS=12,5m
ges: a, h und s
Berechne a:
O=a²+2ahS |Werte einsetzen
470=a² + 2∙a∙12,5
470=a²+25a |-470
o = a² + 25a - 470 |Normalform mit p=25 und q=-470
a1,2 = -12,5
a1 = 12,52 (m) und a2=-37,52 (nicht sinnvoll).
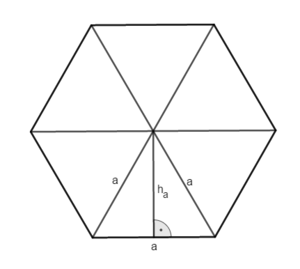
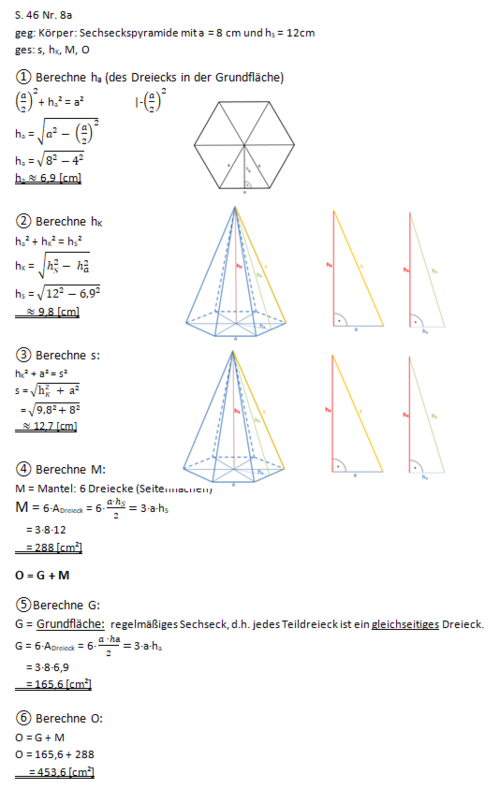
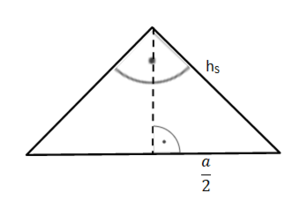
Teildreiecke in der Sechseckspyramide
Um die Höhe ha der Dreiecke in der Grundfläche zu bestimmen, schau den nächsten Tipp an.
Flächeninhalt eines Dreiecks der Grundfläche: ADreieck = ∙a∙ha
Berechne ha mit dem Teildreieck mit den Katheten ha und und der Hypotenuse a.
Skizzen helfen dir, den Überblick zu bewahren.
Lösungen zu den Aufgaben zum Vergleich (falls du die Zwischenwerte nicht im Taschenrechner gespeichert hast, könnte es sein, dass du anders gerundet hast...):
a) s = 12,6 cm; hK = 9,8 cm; M = 288 cm²; O = 454,3 cm²
b) s = 9,9 cm ; hS = 9,4 cm; M = 183,3 cm²; O = 293,1 cm²
c) hK = 27,6 cm ; hS = 34,3 cm; M = 2404,4 cm²; O = 3826,9 cm²
d) a = 31,1 cm; s = 76,6 cm; M = 6997,5 cm²; O =9510,4 cm²
4) Volumen einer Pyramide
Experimentelle Bestimmung der Volumenformel der Pyramide
Du kannst nun auf der Grundlage experimenteller Ergebnisse eine Formel für das Volumen einer Pyramide aufstellen:
Wie viele Pyramidenfüllungen passen in den Quader? _____
Also gilt: VQuader = ___∙ VPyramide |umstellen nach VPyramide
VPyramide =___∙ VQuader
V = ∙ a² ∙hK |∙3
3V = a² ∙ hK |:hK
= a² |
= a
V = ∙ a² ∙hK |∙3
3V = a² ∙ hK |:a²
= hK
Nun setzte die gegebenen Werte für V und a ein und berechne hK
Video mit Beispiel:
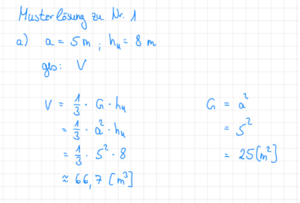
Bestimme die Länge der Grundseite a mit Pythagoras im folgenden Teildreieck: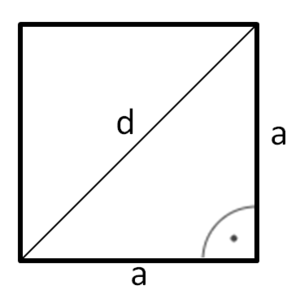
a² + a² = d² Hier kannst du schon den Wert für d einsetzen und dann nach a auflösen:
2a² = 10²
2a² = 100 |:2
a² = 50 |
a 7,1 (cm)
Oder du stellst die Formel nach a um (schwer):
a² + a² = d²
2a² = d² |:2
a² = |
a = |
In der Sechseckspyramide ergeben sich ebenfalls rechtwinklige Dreiecke. Dort kann dann der Satz den Pythagoras angewendet werden, um fehlende Seitenlänge zu bestimmen:
in der Grundfläche
Vergleiche deine Lösungen, es können Rundungsunterschiede auftreten, wenn du mit den gerundeten Werten weitergerechet hast.
a) ha = 13cm (Höhe eines Dreiecks in der Grundfläche); G = 585 cm²; V = 4875 cm³
b) ha = 6,8 cm (Höhe eines Dreiecks in der Grundfläche); G = 161,2 cm²; hK = 9,8 cm (Höhe der Pyramide); V = 526,6 cm³
c) a = 24,9 cm; ha = 21,56 cm; G = 1610,5 cm²; V = 21204,9 cm³
Anwendungsaufgaben
Skizziere zunächst die Pyramide und ergänze die angegebenen Maße a=35m und hK=22m.
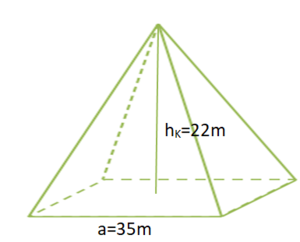
Die Höhe der Dreiecke beträgt hS=28,11m. Bestimme damit den Mantel M.
linkes Dach: ADach=ARechteck mit a = 8m und b = 7,2 m;
rechtes Dach: ADach = MPyramide mit a = 8m und hS = 7,2m.
Bestimme zunächst den Nettopreis G. Der Preis einschließlich der Mehrwertsteuer (19%) ist dann der vermehrte Grundwert G+.
G+ = G∙p+%
mit p+% = 100% + 19% = 119% = 1,19
Erstelle eine Skizze zur Aufgabe und beschrifte sie mit den gegebenen Maßen.
a = 35 m ; hK = 21,65 m.
Die Kantenlänge a ist gegeben und das Volumen (in Liter).
Bestimme den Flächeninhalt der Grundfläche. Dazu musst du zunächst die Höhe der Grundfläche mit dem Satz des Pythagoras in einem geeigneten Teildreieck berechnen.
geg: quadratische Pyramide mit hK = 15 cm und V = 500 cm³ +/- 10%.
10% von 500 cm³ = 50 cm³, also V1 = 500 - 50 = 450 (cm³) und V2 = 500 + 50 = 550 (cm³).
Umfangreiche Übungen findest du auf der Seite Aufgabenfuchs - Pyramide