Benutzer:Buss-Haskert/Terme/Terme vereinfachen: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 42: | Zeile 42: | ||
Erfinde eine Geschichte zu Aufgabe f|2=Tipp zu Nr. 3c, f|3=Verbergen}} | Erfinde eine Geschichte zu Aufgabe f|2=Tipp zu Nr. 3c, f|3=Verbergen}} | ||
{{Box|1=Übung 3|2=Schreibe die Aufgabe aus dem Buch ab in dein Heft. <span style="color:red">Kreise gleichartige Terme mit derselben Farbe ein</span>und vereinfache anschließend. (Das Einkreisen ist PFLICHT! Denke beim Markieren (Einkreisen) daran, dass jeweils das Rechenzeichen und der folgende Term zusammengehören!). | {{Box|1=Übung 3|2=Schreibe die Aufgabe aus dem Buch ab in dein Heft. <span style="color:red">Kreise gleichartige Terme mit derselben Farbe ein</span> und vereinfache anschließend. (Das Einkreisen ist PFLICHT! Denke beim Markieren (Einkreisen) daran, dass jeweils das Rechenzeichen und der folgende Term zusammengehören!). | ||
* S. 102 Nr. 4 | * S. 102 Nr. 4 | ||
* S. 102 Nr. 5 Unterstreiche im Heft den einzusetzenden Term! | * S. 102 Nr. 5 Unterstreiche im Heft den einzusetzenden Term! | ||
Version vom 3. März 2021, 09:38 Uhr
SEITE IM AUFBAU!!
2) Terme vereinfachen
EINSTIEGSAUFGABE NOCH ERGÄNZEN
2.1 Terme addieren und subtrahieren
Übertrage den Merksatz und die nachfolgenden Beispiele in dein Heft (Zeichnungen und Rechnungen):
![]()
x+x+x = 3x
![]()
![]()
x+y+x+y+x = x+x+x+y+y = 3x + 2y
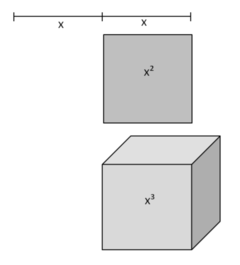
Vorsicht: x, x² und x³ können NICHT zusammengefasst werden, denn sie sind nicht gleichartig!
Bist du noch fit beim Addieren und Subtrahieren von negativen Zahlen?
-s + 3s = 2s Geschichte: Du hast 1€ Schulden und bekommst 3€ Taschengeld. Dann hast du nun 2€ Guthaben.
Zusätzliche Übungsmöglichkeiten findest du in den Learningapps:
2.2 Terme multiplizieren und dividieren
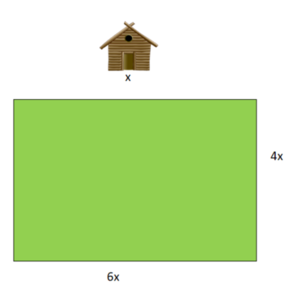
Die Giraffen im Zoo sollen ein neues Außengehege bekommen. Dies soll 6-mal so lang und 4-mal so breit werden wie das Giraffenhaus.
Welche Fläche steht den Giraffen dann außen zur Verfügung?
Länge des Rechtecks: 6x
Breite des Rechtecks: 4x
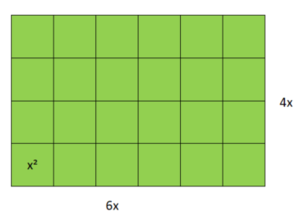
A = 6∙x ∙ 4∙x |sortiere, vertausche die Reihenfolge der Faktoren
= 6∙4∙x∙x |fasse zusammen
= 24x²
Übertrage den Merksatz und die nachfolgenden Beispiele in dein Heft.
Beispiele:
a) a∙a = a²
b) 4b∙0,2b = 4∙0,2∙b∙b = 0,8b²
c) 12x∙7y = 12∙7∙x∙y = 84xy
d) 0,5c∙3d²∙6c = 0,5∙3∙6∙c∙c∙d² = 9c²d²
e) 6ab:3b = = 2∙a (gekürzt)
Überlege "rückwärts": Welcher Term muss mit 7x multipliziert werden, damit das Produkt 28xy beträgt?
Zerlege 28xy in ein Produkt mit dem Faktor 7x:
Multipliziere die Zahlen und Variablen getrennt:
a) 2∙x∙4∙y |Sortiere!
= 2∙4∙x∙y |Berechne das Produkt der Zahlen!
= 8xy Lasse zum Schluss überflüssige Malpunkte weg.
f) t²∙5s∙t∙2s |Sortiere!
= 5∙2∙s∙s∙t²∙t |Berechne das Produkt der Zahlen und fasse die Variablen zu Potenzen zusammen! Erinnerung: t²∙t = t∙t∙t = t³
Multipliziere die Zahlen und Variablen getrennt:
c) 4x∙8xy∙5yb |Sortiere!
= 4∙5∙8∙b∙x∙x∙y∙y |Berechne das Produkt der Zahlen und fasse die Variablen zu Potenzen zusammen!
d) 25ab∙(-40bc)∙(-5c) |Sortiere!
= 25∙(-5)∙(-40)∙a∙b∙b∙c∙c |Berechne das Produkt der Zahlen (Tipp: verliebte Zahlen!) und fasse die Variablen zu Potenzen zusammen!
= -100∙(-40)∙ab²c²
2.3 Vermischte Übungen
|Nun folgen Übungen, bei denen du entscheiden musst, ob Terme addiert/subtrahiert oder multipliziert/dividiert werden. Lies noch einmal die Merksätze auf dieser Seite. Sortiere in der nachfolgenden LearningApp passend.
Unterscheide zwischen den Rechenarten Strichrechung und Punktrechnung! Das Zusammenfassen der Terme ist unterschiedlich!
a) 5+5 = 10 aber 5∙5 = 25
a) a + 2a = 3a Das "hoch 2" bei a ist falsch, denn die Terme werden addiert, also dürfen gleichartige Terme zusammengefasst werden und die Terme a und 2a sind gleichartig, die Variable a bleibt unverändert.
x + x² kann nicht weiter zusammengefast werden, denn die Terme werde addiert, also dürfen nur gleichartige Terme zusammengefasst werden, x und x² sind nicht gleichartig.
c) vgl. b)
d) n²∙2n = 2n³ Die Terme werden multipliziert, daher werden die Zahlen und Variablen getrennt mutlipliziert und die Variablen werden zu Potenzen zusammengefasst, also
n²∙2n = 2∙n²∙n = 2n³
e) 2z² + 2z² = 4z² Die Terme werden addiert, die Terme sind gleichartig und dürfen zusammengefasst werden. Dabei bleibt die Variable z² gleich.
Die Terme werden jeweils addiert, also dürfen gleichartige Terme zusammengefasst werden. Die Terme sind gleichartig, sie heißen nun z.B. "cd" statt nur c.
Die Terme werden jeweils addiert bzw. subtrahiert, es dürfen also gleichartige Terme zusammengefasst werden.
= 5ab - ab + 3mn + 2mn
= 4ba + 5mn